Астронет > Колебания и волны

по текстам по ключевым словам в глоссарии по сайтам перевод

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

Распространение акустических волн конечной амплитуды.

Если возмущения плотности $\delta \rho$ и давления $\delta p$ в акустической волне не являются исчезающе малыми по сравнению с равновесными значениями $\rho _{0}$ и $p_{0},$ то говорят, что волна имеет конечную амплитуду. Обычно такие волны обладают высокой интенсивностью, и для описания их распространения необходимо решать нелинейные уравнения гидродинамики. Анализом распространения волн конечной амплитуды занимается отдельная наука, называемая нелинейной акустикой. В наших лекциях мы ограничимся лишь небольшим объемом сведений из нелинейной акустики.

Пусть в газе вдоль оси Ox распространяется мощная акустическая волна. Если пренебречь вязкостью газа, то одномерное движение частиц вдоль этой оси будет описываться уравнением Эйлера и уравнением непрерывности:

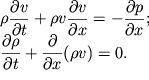$\begin{array}{l} \rho {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + \rho v{\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial p}}{\displaystyle {\displaystyle \partial x}}}; \\ {\displaystyle \frac{\displaystyle {\displaystyle \partial \rho }}{\displaystyle {\displaystyle \partial t}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial x}}}(\rho v) = 0. \\ \end{array}$

(6.35)

Сложность решения этой системы уравнений состоит в том, что в их левых частях содержатся нелинейные члены. Обычно эту нелинейность называют кинематической нелинейностью. Поскольку уравнения (6.35) содержат три неизвестные функции $\rho (x,t),\; p(x,t)$ и $v(x,t),$ то необходимо их дополнить третьим уравнением, связывающим $p$ и $\rho.$ Для газа оно, как уже отмечалось ранее, является уравнением адиабаты:

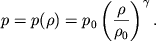$p = p(\rho ) = p_{0} \left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{\gamma }.$

(6.36)

Представим $p$ и $\rho$ в виде:

$p = p_{0} + \delta p; \quad \rho = \rho _{0} + \delta \rho.$

(6.37)

Затем подставим (6.37) в (6.36):

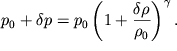$p_{0} + \delta p = p_{0} \left( {\displaystyle 1 + {\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{\gamma }.$

(6.38)

Полагая, что ${\displaystyle \left| {\displaystyle \delta \rho / \rho _{0} } \right|} \lt 1,$ разложим правую часть (6.38) в ряд:

$p_{0} + \delta p = p_{0} {\displaystyle \left[ {\displaystyle 1 + \gamma {\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}} + {\displaystyle \frac{\displaystyle {\displaystyle \gamma \left( {\displaystyle \gamma - 1} \right)}}{\displaystyle {\displaystyle 2}}}\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle \delta \rho }}{\displaystyle {\displaystyle \rho _{0} }}}} \right)^{2} + \ldots} \right]}.$

(6.39)

Пренебрегая членами, имеющими порядок малости $(\delta \rho / \rho _{0} )^{3}$ и выше, окончательно запишем уравнение адиабаты в виде:

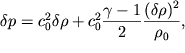$\delta p = c_{0}^{2} \delta \rho + c_{0}^{2} {\displaystyle \frac{\displaystyle {\displaystyle \gamma - 1}}{\displaystyle {\displaystyle 2}}}{\displaystyle \frac{\displaystyle {\displaystyle (\delta \rho )^{2}}}{\displaystyle {\displaystyle \rho _{0} }}},$

(6.40)

где $c_{0}^{2} = \gamma {\displaystyle \frac{\displaystyle {\displaystyle p_{0} }}{\displaystyle {\displaystyle \rho _{0} }}}.$

Второй член в правой части (6.40) начинает давать заметный вклад при сильном сжатии (разрежении), поэтому связь между возмущениями давления $\delta p$ и плотности $\delta \rho$ становится нелинейной. Эта нелинейность обусловлена нелинейностью сил межмолекулярного взаимодействия и называется физической нелинейностью. Она вместе с кинематической нелинейностью может кардинально повлиять на характер распространения интенсивных акустических волн.

Перейдем теперь к установлению основных закономерностей такого распространения. Для этого подставим (6.37) в уравнения (6.35). Тогда получим:

$\begin{array}{l} (\rho _{0} + \delta \rho ){\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} + (\rho _{0} + \delta \rho )v{\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial x}}}; \\ {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta \rho }}{\displaystyle {\displaystyle \partial t}}} + {\displaystyle \frac{\displaystyle {\displaystyle \partial }}{\displaystyle {\displaystyle \partial x}}}[(\rho _{0} + \delta \rho )v] = 0. \\ \end{array}$

(6.41)

Чтобы помочь читателю преодолеть психологический барьер, связанный с анализом системы нелинейных уравнений (6.40) - (6.41), мы покажем вначале, как из этих уравнений можно легко получить волновое уравнение, описывающее линейный режим распространения волн, изученный подробно ранее.

Линейный режим.

$(| \delta \rho |\ll \rho _{0},\; | \delta p| \ll p_{0} ).$

Удержим в уравнениях (6.41) только линейные члены. Тогда получим

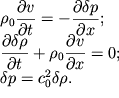$\begin{array}{l} \rho _{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial t}}} = - {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta p}}{\displaystyle {\displaystyle \partial x}}}; \\ {\displaystyle \frac{\displaystyle {\displaystyle \partial \delta \rho }}{\displaystyle {\displaystyle \partial t}}} + \rho _{0} {\displaystyle \frac{\displaystyle {\displaystyle \partial v}}{\displaystyle {\displaystyle \partial x}}} = 0; \\ \delta p = c_{0}^{2} \delta \rho. \\ \end{array}$

(6.42)

Исключим две неизвестные функции, например, $\delta \rho$ и $\delta p.$ Для этого продифференцируем первое уравнение по времени $t,$ а второе - домножим на $c_{0}^{2}$ и продифференцируем по координате $х,$ а затем вычтем одно уравнение из другого. С учетом третьего уравнения члены, содержащие $\delta \rho$ и $\delta p,$ сократятся, и мы получим известное нам волновое уравнение

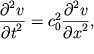${\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}v}}{\displaystyle {\displaystyle \partial t^{2}}}} = c_{0}^{2} {\displaystyle \frac{\displaystyle {\displaystyle \partial ^{2}v}}{\displaystyle {\displaystyle \partial x^{2}}}},$

(6.43)

описывающее распространение без искажений вдоль оси Ox со скоростью $c_{0}$ волны гидродинамической скорости.

Аналогичным образом можно получить волновые уравнения для возмущений давления $\delta p$ и плотности $\delta \rho.$ Не останавливаясь далее на решениях таких уравнений (мы это сделали детально в предыдущих лекциях) перейдем теперь к нелинейному режиму распространения волн конечной амплитуды.

Нелинейный режим.

$(| \delta \rho | \lt \rho _{0},\; | \delta p| \lt p_{0} ).$

Вначале попытаемся качественно описать основные черты нелинейного распространения волн, не прибегая к математике. Наиболее просто это сделать, если обратиться к влиянию физической нелинейности (формула 6.36). Если вспомнить, что скорость звука $c = \sqrt {\displaystyle dp / d\rho },$ то легко понять, что различные части волны могут двигаться с разными скоростями.

На рис. 6.8 изображена зависимость (6.36) и для трех значений плотности $\rho _{0}, \rho _{1}$ и $\rho _{2}$ проведены касательные к графику функции $p = p(\rho ),$ угловые коэффициенты которых равны квадрату скорости распространения волны. Из этого графика можно сделать качественный вывод о том, что чем выше плотность участка волны, тем больше его скорость.

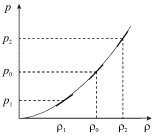Рис. 6.8.

Если, например, гармоническая волна (волна плотности) распространяется вдоль оси Ox (рис. 6.9), то из-за различия скоростей ее разных частей она будет постепенно менять свою форму. На рисунке для простоты показаны лишь три скорости $c_{1} = {\displaystyle \left. {\displaystyle \sqrt {\displaystyle \left( {\displaystyle dp / d\rho } \right)} } \right|}_{\rho _{1} },\; c_{0} = {\displaystyle \left. {\displaystyle \sqrt {\displaystyle \left( {\displaystyle dp / d\rho } \right)} } \right|}_{\rho _{0} }$ и $c_{2} = {\displaystyle \left. {\displaystyle \sqrt {\displaystyle \left( {\displaystyle dp / d\rho } \right)} } \right|}_{\rho _{2} }.$

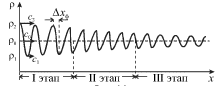Рис. 6.9.

Как показывает опыт, распространение волны можно охарактеризовать тремя этапами.

На I этапе волна трансформируется в пилообразную, обладающую скачком плотности $\rho$ (а также давления $p$ и скорости $v$ ). Эта пилообразная волна приобретает ударный фронт, ширина которого $\Delta x_{ф}$ по мере распространения уменьшается и достигает величины порядка длины свободного пробега молекул газа.

На II этапе происходит нелинейное затухание волны даже при очень малой вязкости и теплопроводности среды. Этот, на первый взгляд, неожиданный эффект связан с переходом в тепло части кинетической энергии молекул, обладающих гидродинамическими скоростями $v$ . Эти молекулы под действием перепадов давления на длине свободного пробега приобретают кинетическую энергию, которая затем переходит в тепло при неупругих столкновениях. Простейший расчет показывает, что энергия, перешедшая в тепло, будет существенно больше, чем на I этапе, когда на ширине $\Delta x_{ф}$ происходили многочисленные столкновения. Естественно, что эта тепловая энергия заимствуется у распространяющейся волны.

III этап связан с возрастающим влиянием вязкости и теплопроводности, которые особенно сильны в областях больших перепадов скорости и температуры (вследствие локального адиабатического нагрева или охлаждения при колебаниях газа). Резкие перепады скорости приводят к возрастанию сил вязкости, а перепады температуры на масштабах порядка длины волны влекут отток тепла из более нагретых областей в менее нагретые. Из-за этих причин часть энергии волны переходит в тепло, и ее амплитуда уменьшается. Поскольку поглощение звука пропорционально квадрату частоты, быстрее затухают волны высших частот, и волна трансформируется в гармоническую волну с исходной (начальной) частотой.

Назад| Вперед

Публикации с ключевыми словами: колебания - волны Публикации со словами: колебания - волны
См. также: Колебания и волны

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце