|
Доказательство теоремы о единственности выпуклого многогранника основано на двух замечательных леммах. Рассмотрим выпуклый многогранник. Отметим некоторые его ребра знаком "+" или "-", а остальные ребра оставим " нейтральными". Выберем какую-нибудь вершину v и, начиная с любого подходящего к ней ребра, последовательно обойдем все ребра, сходящиеся в v, и вернемся к начальному ребру. Если в процессе обхода после очередного ребра с одним знаком следует отмеченное ребро с другим знаком, то мы говорим, что происходит перемена знака. Нейтральные ребра, которые могут находиться между двумя отмеченными ребрами, здесь не учитываются.
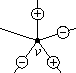 |  |
| а) | б) |
| Рис. 3. |
Обозначим через N(v) общее число перемен знака при обходе вершины v. Так для примера, показанного на рис. 3, а, число перемен знака при обходе вершины v равно четырем, а на рис. 3, б, --- нулю. Так как обход вершины заканчивается в том же ребре, с которого он начинается, число перемен знака четно. В частности, N(v)=0 тогда и только тогда, когда к вершине v не подходит ни одного отмеченного ребра или наряду с нейтральными подходят лишь ребра одного знака.
Лемма 1 (Коши). Пусть на выпуклом многограннике некоторые ребра отмечены знаком "+" или "-". Выделим все те вершины многогранника, к которым подходит хотя бы одно отмеченное ребро. Тогда среди выделенных вершин найдется такая вершина, при обходе которой встретится менее четырех перемен знака.
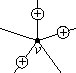
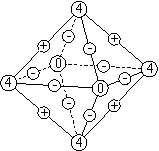 |
| Рис. 4. |
В приведенном на рис. 4 примере расстановки знаков на ребрах октаэдра четыре вершины имеют по четыре перемены знаков и две вершины не имеют перемен знака вообще.
Во второй лемме речь пойдет о выпуклых многоугольниках на плоскости и на сфере. Скажем несколько слов о том, что такое сферический многоугольник.
 |
| Рис. 5. |
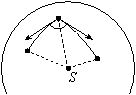
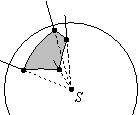
Пусть A1, A2, ..., An --- совокупность точек на сфере. Замкнутая ломаная, состоящая из n дуг больших окружностей A1A2, A2A3, ..., An-1An, AnA1, называется сферическим
многоугольником. Каждая из n дуг A1A2, A2A3, ..., An-1An, AnA1 называется стороной многоугольника A1A2... An. Углом сферического многоугольника называется угол между касательными, проведенными к смежным дугам-сторонам в их общей вершине (рис. 5). Сферический многоугольник называется выпуклым, если он лежит по одну сторону от каждой большой окружности, содержащей его сторону.
 |
| Рис. 6. |
Каждый выпуклый многогранный угол с вершиной S вырезает на сфере с центром S выпуклый сферический многоугольник, сторонами которого являются дуги, по которым грани многогранного угла пересекаются с этой сферой (рис. 6). Заметим, что при этом равным плоским углам многогранного угла соответствуют равные стороны сферического многоугольника, а равным двугранным углам --- равные углы многоугольника.
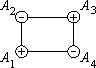
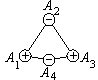
Пусть A1A2... An и B1B2... Bn --- выпуклые, оба плоские (или сферические) n-угольники с соответственно равными сторонами:
A1A2=B1B2, A2A3=B2B3, ..., AnA1=BnB1.
Припишем каждой вершине Ai первого многоугольника знак "+" или "-", в зависимости от того угол при вершине Ai больше или меньше угла при вершине Bi. Если  Ai= Ai= Bi, то вершина Ai остается нейтральной. Bi, то вершина Ai остается нейтральной.
 |  |
| Рис. 7. |
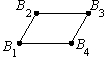
Рассмотрим, например, прямоугольник и параллелограмм с соответственно равными сторонами (рис. 7). Подсчитаем число перемен знака при обходе всех вершин прямоугольника. Это число равно четырем.
Лемма 2 (Коши). Пусть у двух выпуклых n-угольников на плоскости (или на сфере) соответственные стороны равны, а среди соответственных углов имеются неравные. Отметим знаком "+" (или "-") вершины тех углов первого многоугольника, которые строго больше (или меньше) соответствующих углов другого. Тогда число перемен знака при обходе вершин первого многоугольника не меньше четырех.
 |  |
| Рис. 8. |
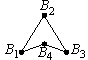
Заметим, что для невыпуклых многоугольников эта лемма не верна (рис. 8).
Из леммы 2 вытекает важное
Следствие. Пусть два выпуклых многогранных угла с одинаковым числом граней имеют соответственно равные плоские углы. Припишем каждому ребру первого многогранного угла знак "+" (или "-"), в зависимости от того двугранный угол при нем больше (или меньше) соответствующего двугранного угла другого многогранного угла. Тогда число перемен знака при обходе ребер первого многогранного угла не меньше четырех.
Действительно, из вершин многогранных углов как из центров опишем сферы одинакового радиуса. Грани многогранных углов вырезают на сферах многоугольники, как на рис. 6. Так как соответственные плоские углы многогранных углов равны, равны соответственные стороны сферических многоугольников. А так как углы многоугольников равны двугранным углам многогранных углов, расстановка знаков на ребрах первого многогранного угла совпадает с расстановкой знаков в вершинах первого многоугольника. Отсюда, по лемме 2, вытекает следствие.
Из этих двух лемм легко получить доказательство теоремы Коши. Допустим, что существуют два неравных выпуклых многогранника M и M' с соответственно равными гранями, взятыми в одинаковом порядке. Это возможно, лишь когда при некоторых соответственных ребрах этих многогранников имеются неравные двугранные углы. Расставим на ребрах многогранника M знаки "+ " и "-", в зависимости от того двугранный угол при данном ребре больше или меньше двугранного угла при соответствующем ребре другого многогранника. При этом соответственные ребра, двугранные углы при которых равны, не получают никакого знака (остаются нейтральными).
Выберем любую вершину v многогранника M, к которой подходит хотя бы одно ребро со знаком. Возьмем многогранный угол многогранника M с вершиной v. По лемме 2, точнее по следствию из нее, число перемен знака при обходе v не меньше четырех. С другой стороны, по лемме 1, среди таких вершин должна быть хотя бы одна, при обходе которой число перемен знака не более двух. Полученное противоречие доказывает теорему. Доказательства лемм 1 и 2 приведены в Приложении.
Следующий раздел
Написать комментарий
|

