Next: Список литературы
Up: Лев Генрихович Шнирельман, антиподы
Previous: Лев Генрихович Шнирельман, антиподы
Contents: Содержание
Пусть 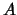 и и 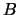 - два
множества натуральных чисел
(натуральный ряд - два
множества натуральных чисел
(натуральный ряд
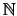 будем считать начинающимся
с единицы). Суммой будем считать начинающимся
с единицы). Суммой 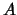 и и 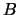 обычно называется множество обычно называется множество 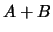 чисел
вида чисел
вида 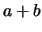 , где , где 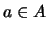 , , 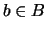 . Нам будет удобнее называть суммой . Нам будет удобнее называть суммой
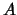 и и 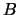 множество множество
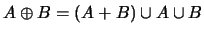 ,
полученное добавлением к ,
полученное добавлением к 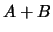 элементов множеств элементов множеств 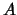 и и 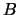 . Скажем,
что множество . Скажем,
что множество 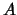 является
базисом натурального ряда, если является
базисом натурального ряда, если
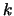 -кратная сумма -кратная сумма
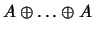 при некотором натуральном при некотором натуральном 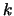 совпадает с натуральным рядом.
Например, если
совпадает с натуральным рядом.
Например, если 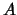 - множество всех квадратов,
то - множество всех квадратов,
то 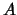 - базис, поскольку - базис, поскольку
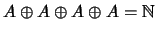 по теореме Лагранжа.
Пусть
по теореме Лагранжа.
Пусть 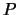 - множество, состоящее из всех простых чисел и единицы. Является
ли - множество, состоящее из всех простых чисел и единицы. Является
ли 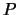 базисом? Положительный ответ на этот вопрос был впервые получен
Шнирельманом: базисом? Положительный ответ на этот вопрос был впервые получен
Шнирельманом: 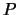 является базисом.
Расскажем об основной идее доказательства. является базисом.
Расскажем об основной идее доказательства.
Сперва введем, следуя Шнирельману, понятие плотности множества
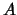 натуральных чисел. Для
каждого натуральных чисел. Для
каждого
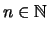 пусть пусть 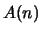 - число
элементов множества - число
элементов множества 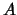 на отрезке на отрезке ![$[1,n]$](http://images.nature.web.ru/nature/2001/01/21/0001159298/img265.gif) . Назовем плотностью . Назовем плотностью
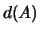 множества множества 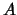 нижнюю грань чисел вида нижнюю грань чисел вида 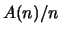 по всем по всем
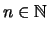 .
Таким образом, плотность - это наибольшее .
Таким образом, плотность - это наибольшее 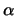 такое, что такое, что
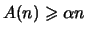 при всех при всех 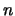 . Шнирельман доказывает следующий результат: . Шнирельман доказывает следующий результат:
Теорема 5. Всякое множество натуральных чисел положительной
плотности является базисом.
Эту теорему нельзя непосредственно применить ко множеству 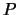 простых чисел с добавленной единицей, поскольку оно имеет нулевую
плотность. (Число
простых чисел с добавленной единицей, поскольку оно имеет нулевую
плотность. (Число  простых чисел,
не превосходящих простых чисел,
не превосходящих 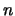 , растет как , растет как 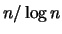 : отношение : отношение
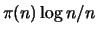 стремится к единице.)
Однако Шнирельман установил, что
стремится к единице.)
Однако Шнирельман установил, что 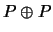 имеет положительную плотность,
откуда вытекает, что имеет положительную плотность,
откуда вытекает, что 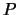 является базисом.
Остается открытым вопрос,
содержит ли является базисом.
Остается открытым вопрос,
содержит ли 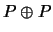 все четные числа (это вариант вопроса Эйлера). все четные числа (это вариант вопроса Эйлера).
Докажем теорему 5. Она вытекает из следующих
лемм 1 и 2.
Лемма 1. Если
 и и 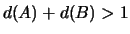 ,
то ,
то
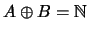 . .
Доказательство.
Зафиксируем
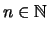 . Если . Если 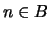 ,
то ,
то
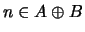 . Если . Если 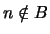 , то рассмотрим два подмножества
отрезка , то рассмотрим два подмножества
отрезка ![$[1,n]$](http://images.nature.web.ru/nature/2001/01/21/0001159298/img265.gif) : :
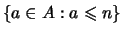 и и
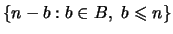 . Они обязаны
пересекаться, поскольку в первом из них не меньше . Они обязаны
пересекаться, поскольку в первом из них не меньше  элементов,
во втором не меньше элементов,
во втором не меньше  элементов
и элементов
и
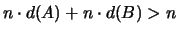 . Следовательно, . Следовательно, 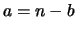 при некоторых при некоторых
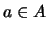 , , 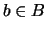 , откуда , откуда
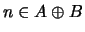 . .
Лемма 2. Для любых
 имеет место неравенство
Шнирельмана: имеет место неравенство
Шнирельмана:

Доказательство.
Положим 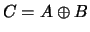 , , 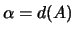 , , 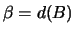 . Зафиксируем . Зафиксируем
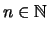 . Нам надо оценить снизу число . Нам надо оценить снизу число  . Пусть . Пусть
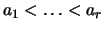 - все элементы множества - все элементы множества 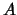 из отрезка из отрезка
![$[1,n]$](http://images.nature.web.ru/nature/2001/01/21/0001159298/img265.gif) , где , где 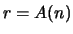 . Отрезок . Отрезок ![$[1,n]$](http://images.nature.web.ru/nature/2001/01/21/0001159298/img265.gif) разбивается числами разбивается числами
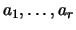 на на 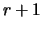 отрезков (некоторые из них могут быть пустыми)
длины отрезков (некоторые из них могут быть пустыми)
длины
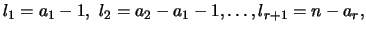 при этом при этом
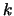 -й отрезок содержит -й отрезок содержит
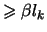 чисел из чисел из 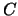 : при : при 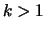 это числа вида
это числа вида  , где , где
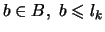 , а при , а при 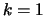 -
это числа из -
это числа из 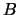 , которые , которые 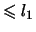 . Отсюда получается оценка . Отсюда получается оценка
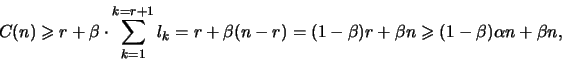
означающая, что
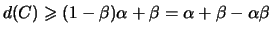 . .
Выведем теорему 5 из лемм 1 и 2.
Неравенство леммы 2 можно переписать в виде
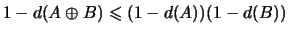 . В таком виде оно распространяется
(по индукции) на любое число слагаемых: . В таком виде оно распространяется
(по индукции) на любое число слагаемых:
 . Пусть теперь . Пусть теперь 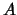 - множество положительной
плотности и - множество положительной
плотности и
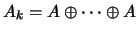 - сумма - сумма 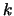 слагаемых, равных слагаемых, равных
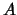 . Предыдущее неравенство показывает, что . Предыдущее неравенство показывает, что 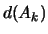 стремится к единице при
возрастании стремится к единице при
возрастании 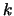 . Пусть . Пусть 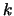 таково, что таково, что 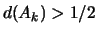 . Из леммы 1 вытекает,
что . Из леммы 1 вытекает,
что
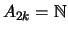 . Таким образом, . Таким образом, 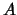 является базисом. Теорема 5 доказана. является базисом. Теорема 5 доказана.
При всяком ли
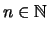 множество
множество
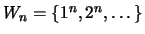 всех всех 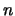 -тых
степеней является базисом? Это - так называемая проблема Варинга.
Она была положительно решена Гильбертом в начале века. Решение оказалось
весьма сложным. Теорема 5 позволяет получить другое решение:
достаточно установить, что -тых
степеней является базисом? Это - так называемая проблема Варинга.
Она была положительно решена Гильбертом в начале века. Решение оказалось
весьма сложным. Теорема 5 позволяет получить другое решение:
достаточно установить, что 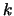 -кратная сумма -кратная сумма
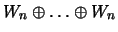 при больших
при больших 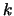 имеет положительную плотность. Элементарное
(хотя очень непростое)
решение проблемы Варинга, основанное на методе Шнирельмана, можно найти в
книжке Хинчина имеет положительную плотность. Элементарное
(хотя очень непростое)
решение проблемы Варинга, основанное на методе Шнирельмана, можно найти в
книжке Хинчина  . .
Вот что пишет Хинчин [5] в связи с леммой 2
(цитируем с сокращениями):
"Осенью
1931 года Л.Г.Шнирельман, рассказывая о своих беседах с Ландау
в Геттингене, сообщил, что они установили следующий интересный факт:
для всех примеров, какие им удавалось придумать, неравенство
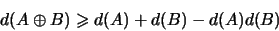
можно было заменить более сильным и более простым неравенством:
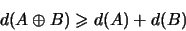
(при условии, что
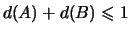 ). Но доказательство этой гипотезы
при первых
попытках не удавалось. Проблема стала модной.
Ученые общества предлагали ее на премию.
Добрая половина английских математиков, отложив все дела, занялась решением
этой задачи. Но она оказалась очень трудной и целый ряд лет не
поддавалась усилиям самых искусных исследователей. Только в 1942 г.,
наконец, с нею справился молодой американский математик Манн".
Доказательство гипотезы Ландау - Шнирельмана можно найти у Хинчина
[5]. Мы очень советуем читателю познакомиться с этой
замечательной книгой. Не менее достойна вашего внимания книга самого
Шнирельмана [7]. Из нее вы узнаете и доказательство
теоремы Лагранжа о сумме четырех квадратов, и решение великой проблемы
Ферма для показателей 3 и 4, и многое другое.
О затронутых здесь темах, касающихся творчества Л.Г.Шнирельмана
см. также [3]. ). Но доказательство этой гипотезы
при первых
попытках не удавалось. Проблема стала модной.
Ученые общества предлагали ее на премию.
Добрая половина английских математиков, отложив все дела, занялась решением
этой задачи. Но она оказалась очень трудной и целый ряд лет не
поддавалась усилиям самых искусных исследователей. Только в 1942 г.,
наконец, с нею справился молодой американский математик Манн".
Доказательство гипотезы Ландау - Шнирельмана можно найти у Хинчина
[5]. Мы очень советуем читателю познакомиться с этой
замечательной книгой. Не менее достойна вашего внимания книга самого
Шнирельмана [7]. Из нее вы узнаете и доказательство
теоремы Лагранжа о сумме четырех квадратов, и решение великой проблемы
Ферма для показателей 3 и 4, и многое другое.
О затронутых здесь темах, касающихся творчества Л.Г.Шнирельмана
см. также [3].
Next: Список литературы
Up: Лев Генрихович Шнирельман, антиподы
Previous: Лев Генрихович Шнирельман, антиподы
Contents: Содержание
Написать комментарий
|

