Эксперимент показывает (см. ниже), что электрон, наряду с орбитальным моментом, имеет собственный момент импульса - спин (от англ. spin), не связанный с его движением в пространстве. Проекция этого момента на заданное направление может принимать только два значения 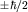 . В общей теории момента (см. п. 7) этому отвечает квантовое число j=1/2. . В общей теории момента (см. п. 7) этому отвечает квантовое число j=1/2.
Таким образом, электрон обладает 4 степенями свободы, и его волновая функция 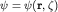 , где дискретная переменная, отвечающая проекции спина на ось z (выбор ее, конечно, условен), , где дискретная переменная, отвечающая проекции спина на ось z (выбор ее, конечно, условен), 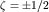 . Иначе говоря, состояние частицы описывается упорядоченной парой функций: . Иначе говоря, состояние частицы описывается упорядоченной парой функций:
Формально это означает, что от пространства квадратично интегрируемых волновых функций H=L2(R3) мы переходим к прямому произведению
где C2 - двумерное комплексное пространство.
Наблюдаемой 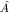 в H отвечает в HS наблюдаемая в H отвечает в HS наблюдаемая 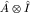 , а , а 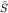 в C2 соответствует в C2 соответствует 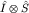 в HS. В пространстве существуют, конечно, и наблюдаемые более общего вида, например, суммы и произведения указанных. В дальнейшем единичные операторы в HS. В пространстве существуют, конечно, и наблюдаемые более общего вида, например, суммы и произведения указанных. В дальнейшем единичные операторы 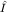 , как правило, мы будем опускать. , как правило, мы будем опускать.
Скалярное произведение в HS определяется в виде
Введем векторный оператор спина
Его компоненты
имеют только два собственных значения 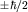 и удовлетворяют коммутационным соотношениям для операторов момента: и удовлетворяют коммутационным соотношениям для операторов момента:
Отсюда следует, что безразмерные эрмитовы 2x2-матрицы 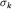 должны удовлетворять условиям должны удовлетворять условиям
где I - единичная матрица.
Еще одно условие мы получим из требования, чтобы проекция спина на любое направление, задаваемое единичным вектором ,
также имела только два СЗ 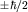 . Это значит, что . Это значит, что
В силу произвольности направления n матрицы 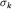 должны удовлетворять соотношению должны удовлетворять соотношению
Указанные три условия эквиваленты одному:
т.е. 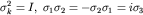 и цикл. пер. и цикл. пер.
Квадрат спина
Это и означает, что спин электрона равен 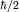 . Заметим, кстати, что операторы . Заметим, кстати, что операторы 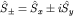 удовлетворяют условию удовлетворяют условию
которое следует из антикоммутативности матриц 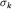 . .
Стандартный выбор матриц 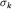 таков: таков:
Они называются матрицами Паули (W. Pauli).
Явные выражения для операторов 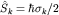 можно получить из общих формул для матричных элементов операторов момента (см. п. 7): можно получить из общих формул для матричных элементов операторов момента (см. п. 7):
Положив здесь 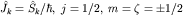 , получим уже известные 2x2-матрицы (нумеруя соответствующим образом строки и столбцы). , получим уже известные 2x2-матрицы (нумеруя соответствующим образом строки и столбцы).
Произвольная наблюдаемая в C2 может быть представлена в виде разложения по 4 линейно независимым базисным эрмитовым матрицам 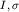 . .
Общие собственные векторы операторов
- диагональных матриц - имеют вид
где 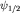 - произвольные функции из L2(R3). Из разложения произвольного вектора состояния в HS, - произвольные функции из L2(R3). Из разложения произвольного вектора состояния в HS,
следует, что вероятность обнаружить при измерении в состоянии  проекцию спина проекцию спина 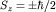
В пространстве C2 волновая функция преобразуется по закону
Сохранение скалярного произведения,
,
приводит к унитарности матриц преобразования:
Следовательно,
Поэтому произвольную унитарную матрицу можно представить в виде
где V - унитарная матрица с detV=1,  - произвольное действительное число. - произвольное действительное число.
Учитывая, что нормированный вектор состояния определен с точностью до фазового преобразования 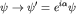 , мы всегда можем ограничиться преобразованиями U с единичным определителем (унимодулярными преобразованиями): , мы всегда можем ограничиться преобразованиями U с единичным определителем (унимодулярными преобразованиями):
Унитарные унимодулярные преобразования в двумерном пространстве C2 образуют, как известно, группу SU(2). Эта группа связана с группой вращений трехмерного евклидова пространства SO(3) следующим образом. Рассмотрим множество эрмитовых бесследовых матриц вида:
где r - действительный трехмерный вектор. Представление группы SU(2) на множестве этих матриц задано так:
Из перестановочных соотношений для матриц Паули 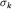 следует, что следует, что
Отсюда и из закона преобразования матриц X находим
Мы получили преобразование в евклидовом пространстве:
где 3x3-матрица R имеет матричные элементы
Используя свойства матриц 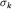 и U, нетрудно показать, что R - действительная ортогональная унимодулярная матрица: и U, нетрудно показать, что R - действительная ортогональная унимодулярная матрица:
т.е. отвечает вращению евклидова пространства: 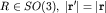 . Матрица . Матрица 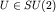 может быть при этом параметризована в виде: может быть при этом параметризована в виде:
где  - угол поворота вокруг оси, заданной единичным вектором n. Здесь учтены легко проверяемые соотношения: - угол поворота вокруг оси, заданной единичным вектором n. Здесь учтены легко проверяемые соотношения:
Мы видим, что матрицы U осуществляют двузначное представление группы вращений SO(3):
Волновая функция электрона в пространстве HS преобразуется при вращении по закону:
где введен оператор полного момента импульса
Рассмотрим движение электрона во внешнем электромагнитном поле, заданном 4-потенциалом 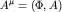 . По принципу соответствия определим гамильтониан (нерелятивистского) электрона (массу его будем обозначать me, чтобы не путать с квантовым числом m для проекции момента) в виде: . По принципу соответствия определим гамильтониан (нерелятивистского) электрона (массу его будем обозначать me, чтобы не путать с квантовым числом m для проекции момента) в виде:
.
Оператор
называют кинетическим импульсом (в классической механике он выражается через скорость частицы: P=mev) в отличие от канонического импульса 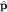 . .
Пусть задано постоянное однородное магнитное поле 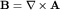 , калибровку потенциала которого выберем в виде , калибровку потенциала которого выберем в виде
Тогда, преобразуя квадрат кинетического импульса
с учетом
получим гамильтониан электрона в постоянном магнитном поле и произвольном электрическом поле  : :
Третье слагаемое в гамильтониане описывает взаимодействие орбитального магнитного момента M электрона с магнитным полем:
Коэффициент пропорциональности между магнитным моментом и моментом импульса называется гиромагнитным отношением
Взаимодействие 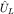 имеет, очевидно, классический аналог, следующий из классической функции Гамильтона частицы. В общем случае протяженной заряженной системы, характеризуемой плотностью электрического тока j(t,r), энергия ее взаимодействия с постоянным магнитным полем A=Bxr/2 в рамках классической электродинамики имеет вид (см. первую часть курса): имеет, очевидно, классический аналог, следующий из классической функции Гамильтона частицы. В общем случае протяженной заряженной системы, характеризуемой плотностью электрического тока j(t,r), энергия ее взаимодействия с постоянным магнитным полем A=Bxr/2 в рамках классической электродинамики имеет вид (см. первую часть курса):
Здесь магнитный момент системы
Для системы N точечных заряженных частиц имеем плотность тока в виде
и магнитный момент
В случае, когда все частицы имеют одинаковое отношение заряда к массе, ea/ma=e/me, получим пропорциональность магнитного и орбитального моментов:
Вычислим магнитный момент  равномерно заряженного по объему шарика радиуса a, вращающегося с постоянной угловой скоростью равномерно заряженного по объему шарика радиуса a, вращающегося с постоянной угловой скоростью  вокруг диаметра. Имеем для плотности заряда и тока вокруг диаметра. Имеем для плотности заряда и тока
где e - полный заряд шарика. Очевидно, что магнитный момент 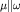 . Тогда получаем . Тогда получаем
При этом магнитный момент пропорционален собственному моменту импульса LS (в системе, где центр шарика массы me покоится):
Назад | Вперед
Посмотреть комментарии[1]
|

