Для электрона в атоме электростатическое взаимодействие значительно сильнее взаимодействия с магнитными полями, достижимыми в лабораторных условиях. Поэтому квадратичным по напряженности поля слагаемым в гамильтониане можно пренебречь:
Пусть магнитное поле направлено по оси z: B=Bez. Учтем сферическую симметрию электростатического потенциала, 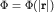 , рассматривая простую модель атома щелочного металла (вспомним школьную химию): один валентный электрон движется в некотором центральном поле, создаваемом кулоновским взаимодействием с ядром и распределенным по объему атома зарядом остальных электронов. Тогда операторы , рассматривая простую модель атома щелочного металла (вспомним школьную химию): один валентный электрон движется в некотором центральном поле, создаваемом кулоновским взаимодействием с ядром и распределенным по объему атома зарядом остальных электронов. Тогда операторы 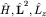 образуют полный набор коммутирующих операторов, т.е. имеют общую систему собственных функций образуют полный набор коммутирующих операторов, т.е. имеют общую систему собственных функций 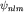 : :
Здесь собственные значения энергии имеет вид
Они связаны с СЗ Enl0 гамильтониана 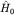 (в отсутствие магнитного поля, B=0), имеющим, очевидно, те же собственные функции, что и (в отсутствие магнитного поля, B=0), имеющим, очевидно, те же собственные функции, что и 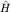 : :
Мы видим, что возникла естественная единица измерения магнитного момента, называемая магнетоном Бора:
где заряд электрона e=-|e|<0.
Ввиду сферической симметрии 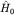 его СЗ Enl0 вырождены с кратностью его СЗ Enl0 вырождены с кратностью 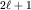 , равной числу возможных значений проекции момента на ось z. Включение магнитного поля нарушает сферическую симметрию системы и приводит к снятию вырождения по квантовому числу m: уровни энергии Enl0 расщепляются на , равной числу возможных значений проекции момента на ось z. Включение магнитного поля нарушает сферическую симметрию системы и приводит к снятию вырождения по квантовому числу m: уровни энергии Enl0 расщепляются на 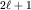 подуровней. подуровней.
Замечание. Для чисто кулоновского потенциала в атоме водорода 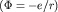 имеется (случайное) вырождение уровней энергии по
имеется (случайное) вырождение уровней энергии по  , которое объясняется дополнительной, кроме сферической, симметрией этого потенциала (см. ниже п. 10). , которое объясняется дополнительной, кроме сферической, симметрией этого потенциала (см. ниже п. 10).
Итак, теория Шредингера предсказывает, что в магнитном поле уровни энергии атома должны расщепляться на нечетное число подуровней, образующих мультиплет. Эксперимент частично подтверждает это предсказание (эффект Зеемана: P. Zeeman, 1896). Расщепление имеет более сложную структуру: оно зависит от типа атома и различно для разных мультиплетов одного и того же атома. В частности, наблюдаются как нечетные, так и четные мультиплеты, как если бы  было полуцелым. было полуцелым.
Более того, обнаруживается тонкая структура уровней даже в отсутствие внешнего магнитного поля. Рассмотрим, например, уровень валентного электрона в щелочном атоме натрия, отвечающий 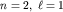 (так называемый 2p-терм). По теории Шредингера имеем вырождение уровня энергии кратности 3.
Эксперимент же показывает, что этот уровень расщеплен на два близких подуровня ( при B=0!). (так называемый 2p-терм). По теории Шредингера имеем вырождение уровня энергии кратности 3.
Эксперимент же показывает, что этот уровень расщеплен на два близких подуровня ( при B=0!).
Особенно наглядно противоречие теории и эксперимента проявилось в опытах Штерна и Герлаха (O. Stern, W. Gerlach, 1922). Они пропускали узкий пучок атомов водорода, находящихся в основном состоянии 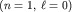 , через область неоднородного магнитного поля и обнаружили, что пучок расщепляется на два пучка. Результаты опытов можно объяснить, предполагая, что атом водорода в основном состоянии обладает некоторым магнитным моментом. Тогда гамильтониан нейтрального атома, рассматриваемого как единая частица с нулевым электрическим зарядом и взаимодействующего с магнитным полем, записывается в виде (ср. выше): , через область неоднородного магнитного поля и обнаружили, что пучок расщепляется на два пучка. Результаты опытов можно объяснить, предполагая, что атом водорода в основном состоянии обладает некоторым магнитным моментом. Тогда гамильтониан нейтрального атома, рассматриваемого как единая частица с нулевым электрическим зарядом и взаимодействующего с магнитным полем, записывается в виде (ср. выше):
где B=B(r) - макроскопически неоднородное магнитное поле. На основе этого гамильтониана можно показать, что если z-компонента поля Bz значительно больше компонент Bx и By, то на атом, влетающий в область поля перпендикулярно оси z, начинает действовать средняя сила
Эксперимент показал, что проекция магнитного момента атома в основном состоянии на заданное направление может принимать только два значения:
где 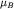 - введенный выше магнетон Бора. Учтем, что в основном состоянии орбитальный момент электрона равен нулю, а масса ядра атома водорода (протона) значительно больше массы электрона. Тогда естественно предположить, что электрон обладает собственным магнитным моментом - введенный выше магнетон Бора. Учтем, что в основном состоянии орбитальный момент электрона равен нулю, а масса ядра атома водорода (протона) значительно больше массы электрона. Тогда естественно предположить, что электрон обладает собственным магнитным моментом  , величина которого равна , величина которого равна 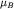 (по определению это максимальное значение проекции (по определению это максимальное значение проекции 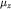 ). При этом магнитный момент электрона пропорционален его собственному моменту импульса (спину) S: ). При этом магнитный момент электрона пропорционален его собственному моменту импульса (спину) S:
где коэффициент пропорциональности gS - спиновое гиромагнитное отношение.
Результаты эксперимента можно интерпретировать так:
где учтено, что gS<0 (e<0).
Заметим, что гипотезу о существовании спина электрона выдвинули Уленбек и Гаудсмит (G. Uhlenbeck, S. Goudsmit, 1925), предложившие модель электрона в виде заряженного шарика, вращающегося вокруг своей оси. Хотя это полуклассическая модель объясняет пропорциональность магнитного и механического моментов (см. выше выражение для магнитного момента вращающегося шарика), но дает неправильное значение спинового гиромагнитного отношения, равное орбитальному, а из эксперимента следует в два раза большее значение. Кроме того, эта модель противоречит теории относительности. Действительно, приравняем магнитный момент шарика магнетону Бора и найдем скорость точки на экваторе:
где 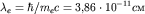 - комптоновская длина волны электрона (см. п. 1). Следовательно, при - комптоновская длина волны электрона (см. п. 1). Следовательно, при 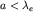 имеем v>2,5c, т.е. больше скорости света в вакууме (!). имеем v>2,5c, т.е. больше скорости света в вакууме (!).
Подчеркнем, что в квантовой механике электрон рассматривается как точечная (бесструктурная) частица. Это подтверждается экспериментом и показывает, в частности, что спин не имеет классического аналога.
Спин в аппарат квантовой механики был введен Паули. Он предложил (постулировал) для описания электрона уравнение, которое теперь называется уравнением Паули (W. Pauli, 1927):
Паулиевский гамильтониан 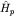 отличается от шредингеровского добавлением слагаемого отличается от шредингеровского добавлением слагаемого 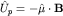 , описывающего взаимодействие с магнитным полем , описывающего взаимодействие с магнитным полем 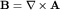 спинового магнитного момента электрона, представляемого оператором спинового магнитного момента электрона, представляемого оператором
Этот оператор введен по аналогии с оператором орбитального магнитного момента 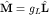 . .
Как уже обсуждалось выше, волновая функция электрона  в теории Паули является двухкомпонентной: в теории Паули является двухкомпонентной:
Она называется спинором и преобразуется при поворотах системы координат по двузначному представлению группы вращений (см. выше). В частности, при повороте на 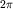 получим преобразование получим преобразование
Следовательно, для спинора этот поворот не эквивалентен тождественному преобразованию, как это имеет место для скаляра и вектора.
Рассмотрим "вывод" уравнения Паули, принадлежащий Фейнману (R.P. Feynman). Из основного соотношения для матриц Паули (см. выше),
следует тождество
где a,b - произвольные векторы.
Учитывая его, запишем гамильтониан электрона в электрическом поле в эквивалентном шредингеровскому виде
Введем теперь взаимодействие с магнитным полем по известному правилу (это, конечно, постулат):
Тогда получим гамильтониан
который эквивалентен гамильтониану Паули:
Действительно, имеем
где второе слагаемое отлично от нуля ввиду некоммутативности компонент оператора кинетического импульса 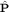 : :
Следовательно,
или
В результате получаем:
т.е. приходим к паулиевскому взаимодействию спинового магнитного момента электрона с магнитным полем.
Назад | Вперед
Посмотреть комментарии[1]
|

