Учтем теперь конечность массы ядра атома. Тогда получаем гамильтониан системы двух частиц - электрона и ядра:
.
Введем новые координаты - относительные и центра масс:
.
Соответствующие операторы импульсов имеют вид:
.
С учетом соотношения
получим гамильтониан в новых переменных:
.
Здесь
- приведенная масса,
- полная масса атома.
В силу![$[\hat H,\hat P]=0$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula403.gif) собственная функция гамильтониана собственная функция гамильтониана  представляется в виде функции, отвечающей движению центра масс с заданным импульсом P, и волновой функции относительного движения представляется в виде функции, отвечающей движению центра масс с заданным импульсом P, и волновой функции относительного движения  : :
.
В системе центра масс (P=0) для  получаем уравнение получаем уравнение
.
В результате мы пришли к уже исследованной задаче: движение частицы массы  в центральном поле U(r) (в нашем случае - неподвижного кулоновского центра в центральном поле U(r) (в нашем случае - неподвижного кулоновского центра 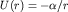 ). Таким образом, как и в классической механике, задача двух тел сводится к задаче одного тела. ). Таким образом, как и в классической механике, задача двух тел сводится к задаче одного тела.
Спектр энергии определяется известной формулой с заменой там массы электрона me на приведенную массу  , т.е. следующей заменой постоянной Ридберга, отвечающей бесконечной массе ядра: , т.е. следующей заменой постоянной Ридберга, отвечающей бесконечной массе ядра:
Уточненный спектр излучения водородоподобного атома принимает вид:
Учет движения ядра позволил объяснить некоторые эффекты. Рассмотрим серии Бальмера (n'=2) обычного водорода H=11H=(p) и его изотопов дейтерия D=21H=(pn) и трития T=31H=(pnn), где в скобках указан протон-нейтронный состав ядер:
Мы видим, что поправки к спектру на конечность массы ядра 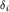 различны для разных изотопов. Следовательно, изотопы могут быть обнаружены спектроскопическими методами, так как их соответствующие спектральные линии немного сдвинуты относительно друг друга. Это и было сделано фактически. Оказалось, что в естественной смеси изотопов, природной воде, относительная концентрация изотопов водорода такова: различны для разных изотопов. Следовательно, изотопы могут быть обнаружены спектроскопическими методами, так как их соответствующие спектральные линии немного сдвинуты относительно друг друга. Это и было сделано фактически. Оказалось, что в естественной смеси изотопов, природной воде, относительная концентрация изотопов водорода такова: 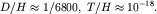
Другое важное приложение теории - объяснение обнаруженной в спектре излучения Солнца спектральной серии Пикеринга. Она приближенно описывается формулой, похожей на формулу Бальмера для атома водорода:
но содержит "лишние" линии, так как квантовое число n1 принимает не только целые, но и полуцелые значения:
которые запрещены для водорода. Правильная интерпретация этой серии была дана, когда более точные спектроскопические измерения показали, что линии несколько сдвинуты по сравнению с водородными линиями так, что в указанной формуле следует сделать замену
Полагая там же n1=n/2, получим формулу, не содержащую полуцелых квантовых чисел:
Она описывает спектральную серию однократно ионизованного атома гелия 42He+=(ppnn), т.е. водородоподобного иона с Z=2.
Пространство состояний одной бесспиновой частицы H=L2(R3), частицы со спином 1/2 (в единицах 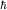 ) - H=L2(R3) ) - H=L2(R3) C2. Для системы частиц имеем соответственно C2. Для системы частиц имеем соответственно
и
Эксперимент показывает, что эта структура пространства состояний справедлива только для систем различных частиц. Волновая функция системы
где
- набор пространственных координат rn и дискретной спиновой переменной 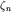 n-ой частицы. Скалярное произведение в этом пространстве n-ой частицы. Скалярное произведение в этом пространстве
В квантовой механике одинаковые частицы принципиально неразличимы. Постулаты теории, сформулированные в п. 4, дополняются новым - принципом тождественности (неразличимости одинаковых частиц).
Принцип тождественности: пространством состояний системы N одинаковых (тождественных) частиц является пространство HS симметричных функций или пространство HA антисимметричных функций.
Определим соответствующие функции 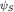 и и 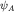 . Для этого рассмотрим группу перестановок N элементов PN. Ее элементы - перестановки . Для этого рассмотрим группу перестановок N элементов PN. Ее элементы - перестановки
причем единичный элемент - тождественная перестановка
а произведение перестановок P2P1 - результат двух последовательных перестановок P1 и P2. В пространстве волновых функций H перестановке P отвечает оператор 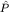 , действующий так: , действующий так:
Очевидно, что 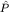 - унитарный оператор и отображение - унитарный оператор и отображение 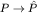 есть представление группы PN в пространстве H.
В H выделяются два инвариантных относительно операторов есть представление группы PN в пространстве H.
В H выделяются два инвариантных относительно операторов 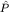 подпространства симметричных и антисимметричных функций: подпространства симметричных и антисимметричных функций:
Эти функции - собственные функции операторов перестановки:
Здесь введена четность перестановки 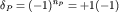 для четного (нечетного) числа nP последовательных перестановок двух частиц, к которым сводится данная перестановка P. для четного (нечетного) числа nP последовательных перестановок двух частиц, к которым сводится данная перестановка P.
Очевидно, что 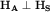 . В случае N=2 имеем . В случае N=2 имеем
Действительно,
При 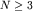 имеются и другие, более сложные, чем HA и HS, инвариантные подпространства, но они не имеют физических приложений. имеются и другие, более сложные, чем HA и HS, инвариантные подпространства, но они не имеют физических приложений.
Частицы, описываемые функциями 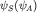 , называются бозонами (фермионами) и подчиняются статистике Бозе - Эйнштейна (Ферми - Дирака). , называются бозонами (фермионами) и подчиняются статистике Бозе - Эйнштейна (Ферми - Дирака).
В квантовой механике постулируется следующая связь спина и статистики: частицы с целым спином (s=0,1,2,...) являются бозонами, частицы с полуцелым спином (s=1/2,3/2,5/2,...) - фермионами.
Замечание. В квантовой теории поля указанная связь спина и статистики представляет собой теорему, доказанную В. Паули (W. Pauli, 1940) на основе принципа причинности и лоренц-инвариантности.
Статистика составных тождественных частиц (например, атомных ядер) определяется четностью числа входящих в их состав фермионов. Например, дейтрон ( ядро атома дейтерия D=21H=(pn)), состоящее из двух частиц со спином 1/2, протона и нейтрона, является бозоном.
Гамильтониан системы N тождественных попарно взаимодействующих частиц массы m во внешнем поле V(r) имеет вид:
где U - потенциал парного взаимодействия. В силу одинаковости масс частиц и независимости потенциалов V и U от номеров частиц оператор перестановки 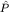 - интеграл движения: - интеграл движения:
Следовательно, в процессе эволюции системы согласно уравнению Шредингера
тип симметрии волновой функции не изменяется. Иначе говоря, связь спина и статистики не разрушается динамикой, как и должно быть в непротиворечивой теории.
Рассмотрим важный частный случай системы невзаимодействующих частиц (U=0) во внешнем поле. Гамильтониан такой системы представляется в виде суммы гамильтонианов отдельных частиц:
Решение стационарного уравнения Шредингера, 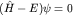 , можно искать в виде произведения одночастичных волновых функций: , можно искать в виде произведения одночастичных волновых функций:
Функция 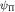 не удовлетворяет принципу тождественности, хотя и является решением УШ. Поскольку оператор перестановки - интеграл движения, то функция не удовлетворяет принципу тождественности, хотя и является решением УШ. Поскольку оператор перестановки - интеграл движения, то функция 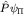 - также решение УШ: - также решение УШ:
Поэтому правильные решения определенной симметрии 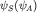 получаются путем составления (анти)симметричных линейных комбинаций функций получаются путем составления (анти)симметричных линейных комбинаций функций 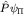 . .
Назад | Вперед
Посмотреть комментарии[1]
|

