




Up: HST and the
Previous: The HST Key
Science with the Hubble Space Telescope -- II
Book Editors: P. Benvenuti, F. D. Macchetto, and E. J. Schreier
Electronic Editor: H. Payne
G.A. Tammann, L. Labhardt & M. Federspiel
Astronomisches Institut der Universität Basel, Venusstr. 7,
CH-4102 Binningen, Switzerland
A. Sandage
The Observatories of the Carnegie Institution, 813 Santa Barbara
Street, Pasadena, CA 91101, USA
A. Saha, F.D. Macchetto & N. Panagia
Space Telescope Science Institute
3700 San Martin Drive, Baltimore, MD 21218, USA
Abstract:
HST has so far provided Cepheid distances to nine galaxies. Although
not sufficient yet to determine the distance of the extended Virgo
cluster, they are decisive for the distance scale in two ways. (1) Seven of
the galaxies contribute to a much improved calibration of the Tully-Fisher
relation. Applying this to a complete sample of Virgo spirals one
obtains a cluster distance of 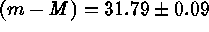 . Other distance
indicators support this value. The adopted linear distance of
. Other distance
indicators support this value. The adopted linear distance of  Mpc combined with the cluster velocity of
Mpc combined with the cluster velocity of  (in the CMB frame) gives
(in the CMB frame) gives  (internal error). (2) Six of the
galaxies have been the site of seven SNe Ia with well observed maxima. Their
resulting calibration in absolute magnitudes gives
(internal error). (2) Six of the
galaxies have been the site of seven SNe Ia with well observed maxima. Their
resulting calibration in absolute magnitudes gives 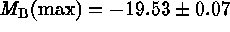 and
and 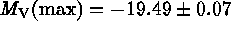 with
negligible intrinsic scatter. If this calibration is used to
determine the distances of all distant SNe Ia with known maxima and
with
with
negligible intrinsic scatter. If this calibration is used to
determine the distances of all distant SNe Ia with known maxima and
with 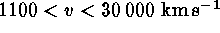 ,
, 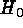 becomes
becomes 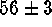 (internal error). Systematic errors tend to make this an upper limit; in
particular, the case
(internal error). Systematic errors tend to make this an upper limit; in
particular, the case 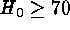 can be excluded.---The conclusion is that
the large-scale value of the Hubble constant is
can be excluded.---The conclusion is that
the large-scale value of the Hubble constant is 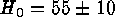 (external
error).
(external
error).
The influence of HST on the determination of  is already
enormous and it can only grow. In Table 1 a compilation is given of
distance determinations with HST having some bearing on
is already
enormous and it can only grow. In Table 1 a compilation is given of
distance determinations with HST having some bearing on 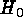 . The
values scatter between 55 and 80 and the formal mean is
. The
values scatter between 55 and 80 and the formal mean is 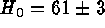 .
This, however, is not the best value, because some values shown are
mutually incompatible.
.
This, however, is not the best value, because some values shown are
mutually incompatible.
There are now two self-consistent routes to 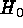 to which HST has
heavily contributed. The first route via the Virgo cluster is
described in Section 2, the second route using supernovae of type Ia
(SNe Ia) is discussed in Section 3.
to which HST has
heavily contributed. The first route via the Virgo cluster is
described in Section 2, the second route using supernovae of type Ia
(SNe Ia) is discussed in Section 3.
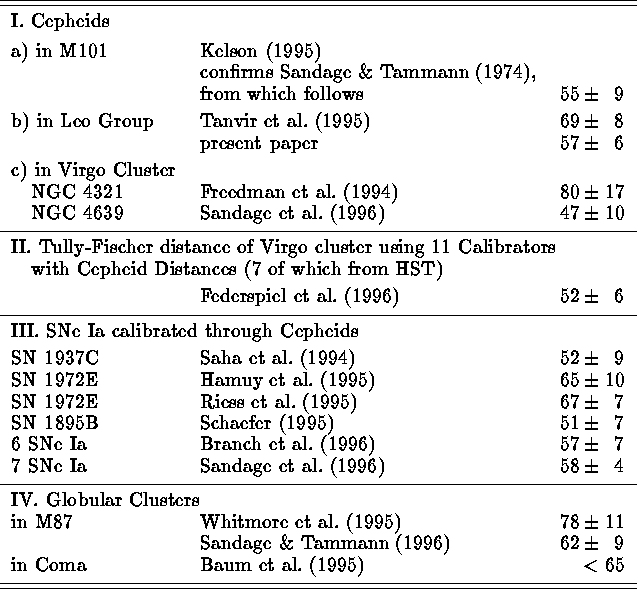
Table 1: 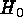 determinations from HST
determinations from HST
Much of what follows depends on Cepheid distances. A word on the
reliability of their P-L relation is, therefore, in place. The P-L
relation of Madore & Freedman (1991), adopted in the following,
assumes an LMC modulus of 18.50. Actual confirmation of this value to
better than 0.10 mag comes from the P-L relation calibrated by
Galactic Cepheids (Sandage & Tammann 1968, Feast & Walker 1987) and
independently from the ring of SN 1987A (Panagia et al. 1991, Gould
1994); further support is given by RR Lyr stars and other distance
determinations (cf. Tammann 1996). The zero point of the adopted P-L
relation is therefore secure to 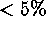 in linear distance. The slope
of the relation is well determined by the LMC Cepheids; it is of less
importance as long as the Cepheids under consideration cover a
sufficient period range, which is also needed to avoid selection
effects (Sandage 1988). Metallicity effects are believed to be small
(Freedman & Madore 1990, Chiosi et al. 1993).
in linear distance. The slope
of the relation is well determined by the LMC Cepheids; it is of less
importance as long as the Cepheids under consideration cover a
sufficient period range, which is also needed to avoid selection
effects (Sandage 1988). Metallicity effects are believed to be small
(Freedman & Madore 1990, Chiosi et al. 1993).
When the first reliable Cepheid distance of a Virgo galaxy (NGC 4321)
became available from HST (Freedman et al. 1994), it was
precipitately hailed the Virgo cluster distance (Mould et
al. 1995, Kennicutt et al. 1995) although the value of 17 Mpc was
suspiciously low. The next two Virgo galaxies, NGC 4536 (Saha et
al. 1996a) and NGC 4496A (Saha et al. 1996b), again had very low
distances. Only the fourth galaxy, NGC 4639, revealed the
important depth of the cluster (note for comparison: the spiral
members span 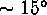 in the sky!). Its distance is 25 Mpc
(Sandage et al. 1996) and yet it is a bona fide cluster member; with a
small velocity of 800 kms
in the sky!). Its distance is 25 Mpc
(Sandage et al. 1996) and yet it is a bona fide cluster member; with a
small velocity of 800 kms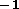 , it cannot be assigned to the
background.
, it cannot be assigned to the
background.
It is no accident that the first three Virgo spirals with Cepheid
distances lie on the near side of the cluster. They were selected from
Sandage & Bedke's (1988) atlas of galaxies most suited for HST;
they were thus biased to begin with. NGC 4639 looks much more
difficult and would not have been selected had it not produced the
archetypal SN 1990N.
It is now clear that it will take at least a dozen Cepheid distances
of a randomly selected sample of Virgo members to obtain a meaningful
mean cluster distance.
Meanwhile Tanvir et al. (1995) have suggested to step up their
Cepheid-based Leo group distance of 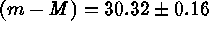 out to the
Virgo cluster by means of relative distance determinations. The
best available relative distances are compiled in Table 2. Adding the
mean difference of
out to the
Virgo cluster by means of relative distance determinations. The
best available relative distances are compiled in Table 2. Adding the
mean difference of  to the above distance
modulus gives a Virgo cluster modulus of
to the above distance
modulus gives a Virgo cluster modulus of 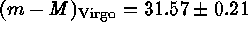 .
For brevity we will refer to this value in the following as the
Cepheid distance of the Virgo cluster .
.
For brevity we will refer to this value in the following as the
Cepheid distance of the Virgo cluster .

Table 2: The distance modulus difference between the Leo group
and the Virgo cluster
There are now 11 spiral galaxies with Cepheid distances (seven of which
come from HST) which are useful for the calibration of the relation
between absolute magnitude and  (w= inclination-corrected 21cm-line
width). Two close companions of M101 bring the number of useful calibrators
to 13 (cf. Table 3). Two galaxies (M101 and M100) are less inclined than
the frequently adopted limit of
(w= inclination-corrected 21cm-line
width). Two close companions of M101 bring the number of useful calibrators
to 13 (cf. Table 3). Two galaxies (M101 and M100) are less inclined than
the frequently adopted limit of 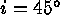 ; yet their inclinations are
so well defined by mapping their velocity field that they are still useful
as calibrators.
; yet their inclinations are
so well defined by mapping their velocity field that they are still useful
as calibrators.
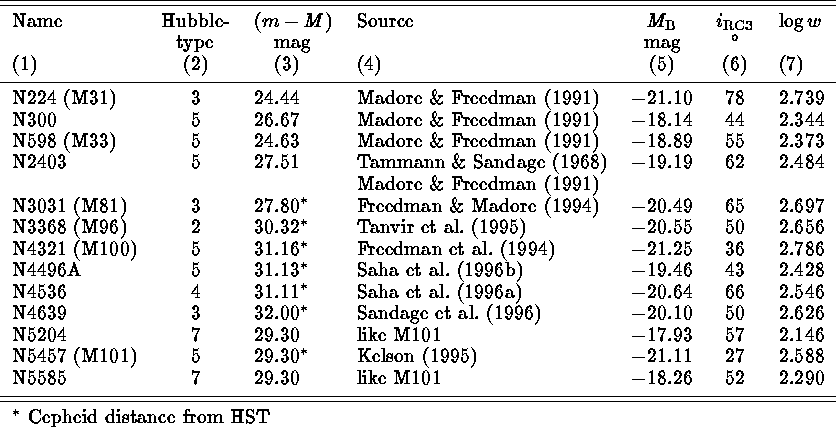
Table 3: Galaxies with Cepheid distances for the
calibration of the Tully-Fisher relation
The date in Table 3 yield the following calibration of the TF relation
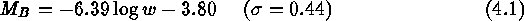
(Federspiel et al. 1996), where the slope is taken from the Virgo cluster.
An objective and complete sample of Virgo spirals is
defined by the 48 non-peculiar galaxies of type Sab--Sdm from the
Virgo Cluster Catalog (Binggeli et al. 1985) with  and
lying within the isopleths of substructures A and B (see Binggeli et
al. 1993) or, without changing the result, within the X-ray contour of
the cluster (Böhringer et al. 1994). This sample together with
equation (1) gives
and
lying within the isopleths of substructures A and B (see Binggeli et
al. 1993) or, without changing the result, within the X-ray contour of
the cluster (Böhringer et al. 1994). This sample together with
equation (1) gives 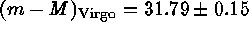 . The use of infrared
instead of B magnitudes does not bring an advantage (Schröder
1995), nor does the application of the inverse TF relation. For
the robustness of the result against variations of the input
parameters the reader is referred to Federspiel et al. (1996).
. The use of infrared
instead of B magnitudes does not bring an advantage (Schröder
1995), nor does the application of the inverse TF relation. For
the robustness of the result against variations of the input
parameters the reader is referred to Federspiel et al. (1996).
The peak of the luminosity function (LF) of globular clusters
(GC) has frequently been used as a standard candle. A modern
calibration of the GCs in the Galaxy and in M31 combined with a
compilation of published GCLFs in five Virgo ellipticals has led to a
Virgo modulus of  (Sandage & Tammann
1995). Meanwhile Whitmore et al. (1995) found a very bright peak
magnitude in V and I for NGC 4486, which is well determined with
HST and which corresponds, with our precepts, to a modulus of
(Sandage & Tammann
1995). Meanwhile Whitmore et al. (1995) found a very bright peak
magnitude in V and I for NGC 4486, which is well determined with
HST and which corresponds, with our precepts, to a modulus of
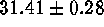 (Sandage & Tammann 1996). However, the GCs in
NGC 4486 have a bimodal color distribution which is suggestive of age
differences and possible merger effects (Fritze-von Alvensleben 1995,
Elson & Santiago 1996). Turning a blind eye to this problem and
averaging over all available GCLFs in Virgo we obtain
(Sandage & Tammann 1996). However, the GCs in
NGC 4486 have a bimodal color distribution which is suggestive of age
differences and possible merger effects (Fritze-von Alvensleben 1995,
Elson & Santiago 1996). Turning a blind eye to this problem and
averaging over all available GCLFs in Virgo we obtain
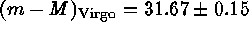 . We are aware that the method may still
face considerable problems.
. We are aware that the method may still
face considerable problems.
The  method, normally applied to ellipticals, was extended
to the bulges of S0 and spiral galaxies by Dressler (1987). Using the bulges
of the Galaxy, M31, and M81 as local calibrators, one obtains
method, normally applied to ellipticals, was extended
to the bulges of S0 and spiral galaxies by Dressler (1987). Using the bulges
of the Galaxy, M31, and M81 as local calibrators, one obtains 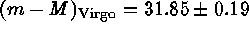 (Tammann 1988).
(Tammann 1988).
Novae are potentially powerful distance indicators through their
luminosity-decline rate relation. Using the Galactic calibration of
Cohen (1985), Capaccioli et al. (1989) have found the apparent
distance modulus of M31 to be 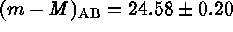 (i.e., somewhat less than indicated by Cepheids). From six novae in
three Virgo ellipticals Pritchet & van den Bergh (1987) concluded
that the cluster is more distant by
(i.e., somewhat less than indicated by Cepheids). From six novae in
three Virgo ellipticals Pritchet & van den Bergh (1987) concluded
that the cluster is more distant by 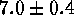 mag than the apparent
modulus of M31, implying
mag than the apparent
modulus of M31, implying 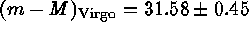 (zero
absorption is adopted for the Virgo cluster, see Section 2.6). The
result carries still small weight, but is interesting because it is
based on novae exclusively. HST observations, although
time-consuming, of novae in the Virgo cluster could much improve this
independent result.
(zero
absorption is adopted for the Virgo cluster, see Section 2.6). The
result carries still small weight, but is interesting because it is
based on novae exclusively. HST observations, although
time-consuming, of novae in the Virgo cluster could much improve this
independent result.
Theoretical models of SNe Ia by various authors converge towards
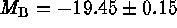 for ``Branch normal'' objects (Branch 1996,
Höflich & Khokhlov 1996, Ruiz-Lapuente 1996). It is true that fainter,
nearby SNe Ia are known, but being red and spectroscopically peculiar they
can easily be singled out, and they do not contaminate distant,
luminosity-selected samples of SNe Ia (cf. Section 3). Eight SNe Ia which
have occurred in the Virgo cluster have
for ``Branch normal'' objects (Branch 1996,
Höflich & Khokhlov 1996, Ruiz-Lapuente 1996). It is true that fainter,
nearby SNe Ia are known, but being red and spectroscopically peculiar they
can easily be singled out, and they do not contaminate distant,
luminosity-selected samples of SNe Ia (cf. Section 3). Eight SNe Ia which
have occurred in the Virgo cluster have 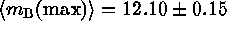 mag. This value combined with the theoretical calibration
gives
mag. This value combined with the theoretical calibration
gives 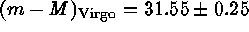 .---Had we used instead the
empirical calibration of Table 5 below, the Virgo modulus would have become
larger by 0.08 mag. We refrain from using this value because the routes
towards
.---Had we used instead the
empirical calibration of Table 5 below, the Virgo modulus would have become
larger by 0.08 mag. We refrain from using this value because the routes
towards 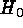 in Sections 2 and 3 are to be kept strictly apart.
in Sections 2 and 3 are to be kept strictly apart.
The assumption that the LF of the shells of planetary nebulae
(PN) in the light of the 5007Å line had a universal cutoff at
 mag has led to a Virgo modulus significantly lower
than obtained from the six methods discussed above (Jacoby et
al. 1990). Yet it was pointed out that the cutoff magnitude depends
on the sample size (i.e., the absolute magnitude of the parent galaxy;
Bottinelli et al. 1991, Tammann 1993). Numerically simulated LFs of
the shell luminosities confirm, indeed, the dependence on sample size
and population age (Méndez et al. 1993). As a consequence, the
published PN distances deviate systematically from the Cepheid
distances. The deviations increase with distance from M81 (Jacoby
et al. 1989), NGC 5253 (Jacoby & Ciardullo 1993), and the Leo
group (Ciardullo et al. 1989) to reach at the Virgo cluster
(Jacoby et al. 1990) 0.74 mag !---A new method to derive PN
distances, allowing for sample size and other effects, has been
proposed by Soffner et al. (1995); the first result for the nearby
galaxy NGC 300 is encouraging.
mag has led to a Virgo modulus significantly lower
than obtained from the six methods discussed above (Jacoby et
al. 1990). Yet it was pointed out that the cutoff magnitude depends
on the sample size (i.e., the absolute magnitude of the parent galaxy;
Bottinelli et al. 1991, Tammann 1993). Numerically simulated LFs of
the shell luminosities confirm, indeed, the dependence on sample size
and population age (Méndez et al. 1993). As a consequence, the
published PN distances deviate systematically from the Cepheid
distances. The deviations increase with distance from M81 (Jacoby
et al. 1989), NGC 5253 (Jacoby & Ciardullo 1993), and the Leo
group (Ciardullo et al. 1989) to reach at the Virgo cluster
(Jacoby et al. 1990) 0.74 mag !---A new method to derive PN
distances, allowing for sample size and other effects, has been
proposed by Soffner et al. (1995); the first result for the nearby
galaxy NGC 300 is encouraging.
Surface brightness fluctuations (SBF) have also been proposed as
distance indicators (Tonry & Schneider 1988). The first ``test'' has
remained rather unconvincing, spreading the elliptical Virgo
cluster members over an interval of 12 to 24 Mpc (Tonry et al. 1990);
this interval was interpreted as real although early-type galaxies are
known to be concentrated in the cores of galaxy clusters.
Moreover, the individual distances correlate with the Mg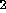 index
(Lorenz et al. 1993). Finally, we note that the SBF distances of
NGC 5253 (Phillips et al. 1992), the Leo group (Tonry 1991), and the
Virgo cluster (Tonry 1991) are smaller than Cepheid distances by as
much as 0.97, 0.48, and 0.56 mag, respectively.
index
(Lorenz et al. 1993). Finally, we note that the SBF distances of
NGC 5253 (Phillips et al. 1992), the Leo group (Tonry 1991), and the
Virgo cluster (Tonry 1991) are smaller than Cepheid distances by as
much as 0.97, 0.48, and 0.56 mag, respectively.
For the stated reasons we use neither the PN nor the SBF distances.
A census of the
Virgo cluster containing almost 2000 certain and possible members (Binggeli
et al. 1985) reveals a complex structure with two main subclusters A and B
and additional concentrations some of which, particularly in the
southwestern part, are more distant. To obtain a genuine cluster sample we
restrict the sample to the 364 galaxies with known redshifts lying within
the outer isopleths of subclusters A and B (Binggeli et al. 1993; the
individual galaxies are listed there). Their mean velocity is  (with respect to the Local Group
centroid). If one considers instead the 361 galaxies within the very
similar X-ray contour of the cluster (Böhringer et al. 1994), the mean
velocity becomes
(with respect to the Local Group
centroid). If one considers instead the 361 galaxies within the very
similar X-ray contour of the cluster (Böhringer et al. 1994), the mean
velocity becomes 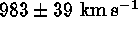 . Taking all 385 galaxies
with redshifts in the Virgo survey area, excluding only background objects,
we find
. Taking all 385 galaxies
with redshifts in the Virgo survey area, excluding only background objects,
we find 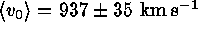 . From this we
adopt a best cluster velocity of
. From this we
adopt a best cluster velocity of 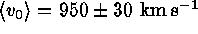 . This result supersedes an early value of
. This result supersedes an early value of  (Huchra 1988) which was based on only 250
galaxies and a less well defined area.
(Huchra 1988) which was based on only 250
galaxies and a less well defined area.
To obtain the cosmic recession velocity of the Virgo cluster, the
observed value must still be corrected for the deceleration of the Local
Group. We adopt 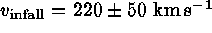 (cf. Tammann
1996) and find for Virgo
(cf. Tammann
1996) and find for Virgo 
Yet we prefer a very similar value the rational of which, however, is quite
different. Many authors step up the Virgo distance out to the Coma cluster
using the relative distance modulus between Virgo and Coma, and find
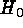 at the distance of Coma. One can repeat that with any cluster whose
distance relative to Virgo is known. In fact there are at least 14 clusters
with rather good relative distances and velocities
at the distance of Coma. One can repeat that with any cluster whose
distance relative to Virgo is known. In fact there are at least 14 clusters
with rather good relative distances and velocities  (
( is the velocity in the frame
of the microwave background). The best cosmic value of
is the velocity in the frame
of the microwave background). The best cosmic value of  is then the
all-sky mean over 14 different
is then the
all-sky mean over 14 different  determinations. But more elegant is
the reverse method: the relative distances are used to scale down the
velocities of the 14 clusters and to predict a mean Virgo cluster velocity,
i.e., the
determinations. But more elegant is
the reverse method: the relative distances are used to scale down the
velocities of the 14 clusters and to predict a mean Virgo cluster velocity,
i.e., the 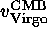 velocity which the cluster would have in
the absence of all local deviations from an ideal expansion field. The
result of this procedure is
velocity which the cluster would have in
the absence of all local deviations from an ideal expansion field. The
result of this procedure is 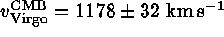 (Sandage & Tammann 1990, Jerjen & Tammann 1993, Jerjen 1995
for a more rigid error determination).
(Sandage & Tammann 1990, Jerjen & Tammann 1993, Jerjen 1995
for a more rigid error determination).
The six independent distance determinations of the Virgo cluster in Sections
2.1--2.3 are repeated in Table 4.
All distance moduli are taken to be true values, i.e., zero absorption
is assumed towards the Virgo cluster. If the B-absorption implied by
Burstein & Heiles (1984) is applied individually to all galaxies used
for the distance determinations, the modulus becomes lower by only
0.06 mag. Even this almost negligible amount may be an overestimation
as discussed by Sandage & Tammann (1996).

Table 4: Distance moduli of the Virgo cluster
If the adopted mean cluster distance of  Mpc is combined with
Mpc is combined with
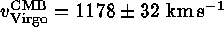 one obtains
one obtains

An HST program has been mounted to determine the large-scale value
of 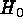 . The aim is to derive Cepheid distances (in V and I to
control absorption effects) of up to ten galaxies which have produced
well observed SNe Ia. So far we have calibrated the peak luminosity of
six SNe Ia. A seventh object has become available through Tanvir's et
al. (1995) Cepheid distance of the Leo group. (It can be assumed that
the member galaxies of this compact group lie practically at the same
distance.) The resulting absolute magnitudes of the seven SNe Ia are
shown in Table 5. Detailed discussions of the input parameters are
given elsewhere (Sandage et al. 1996, Tammann et al. 1996;
negligible differences between these sources are due to a different
weighting of individual sources). The agreement to within the errors
between the individual luminosities supports the claim that SNe Ia are
(nearly) perfect standard candles. Independent confirmation of the
luminosities comes from Höflich et al. (1996) who have three SNe Ia
in common with Table 5. Their model luminosities are the same
to within
. The aim is to derive Cepheid distances (in V and I to
control absorption effects) of up to ten galaxies which have produced
well observed SNe Ia. So far we have calibrated the peak luminosity of
six SNe Ia. A seventh object has become available through Tanvir's et
al. (1995) Cepheid distance of the Leo group. (It can be assumed that
the member galaxies of this compact group lie practically at the same
distance.) The resulting absolute magnitudes of the seven SNe Ia are
shown in Table 5. Detailed discussions of the input parameters are
given elsewhere (Sandage et al. 1996, Tammann et al. 1996;
negligible differences between these sources are due to a different
weighting of individual sources). The agreement to within the errors
between the individual luminosities supports the claim that SNe Ia are
(nearly) perfect standard candles. Independent confirmation of the
luminosities comes from Höflich et al. (1996) who have three SNe Ia
in common with Table 5. Their model luminosities are the same
to within 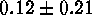 mag. Branch's (1996) model luminosity of SN
1981B agrees fortuitously well with ours, and two SNe Ia of
Ruiz-Lapuente (1996) are fainter by only
mag. Branch's (1996) model luminosity of SN
1981B agrees fortuitously well with ours, and two SNe Ia of
Ruiz-Lapuente (1996) are fainter by only  mag judging
from their late spectra and the inferred
mag judging
from their late spectra and the inferred  Ni mass.
Ni mass.
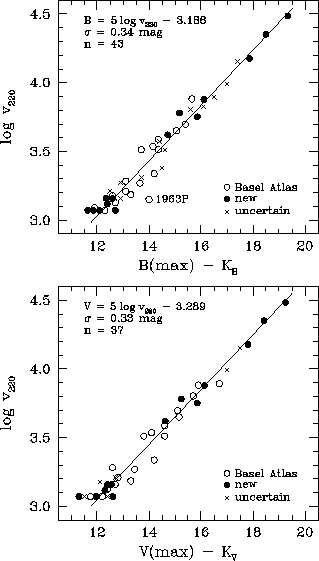
Figure: Hubble diagrams in B and V of all non-red SNe Ia with
known maximum magnitudes. Open circles and crosses are from the
older archive literature. Filled circles are the modern data provided by
Phillips (1993) and Hamuy et al. (1995). The very small K-corrections
are applied.
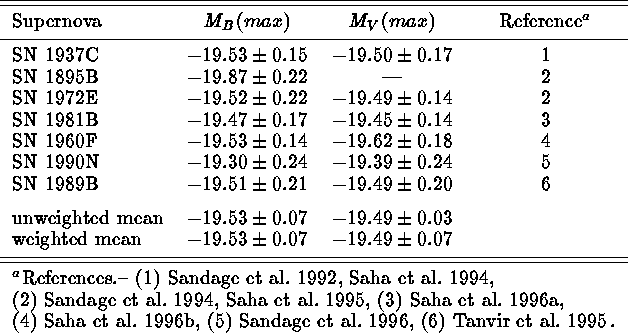
Table 5: Absolute Magnitudes of SNe Ia at Maximum.
The Hubble diagram of all SNe Ia beyond 1100 kms with
reasonably well determined maximum magnitudes is shown in Fig. 1
(Tammann & Sandage 1995). Their intrinsic luminosity scatter
must be considerably less than 0.35 mag, because much of the scatter
is expected from observational errors and peculiar motions. Indeed, the
intrinsic scatter must be very small because even the most distant SNe
Ia lie very close to the theoretical Hubble line of slope 0.2. The
argument goes as follows. The most distant SNe Ia occupy a volume
about 18000 times larger than that of the local calibrators. The
large volume must contain exceptionally luminous SNe Ia---if they
existed---and they have a much enhanced discovery chance for two
reasons: their apparent magnitude is brighter than average and
they stay longer above the detection limit. But still, there are no
objects significantly above the Hubble line, not even at large
distances. This means: The sample of SNe Ia shown in Fig. 1
constitutes a homogeneous class of very luminous and unabsorbed
objects.
with
reasonably well determined maximum magnitudes is shown in Fig. 1
(Tammann & Sandage 1995). Their intrinsic luminosity scatter
must be considerably less than 0.35 mag, because much of the scatter
is expected from observational errors and peculiar motions. Indeed, the
intrinsic scatter must be very small because even the most distant SNe
Ia lie very close to the theoretical Hubble line of slope 0.2. The
argument goes as follows. The most distant SNe Ia occupy a volume
about 18000 times larger than that of the local calibrators. The
large volume must contain exceptionally luminous SNe Ia---if they
existed---and they have a much enhanced discovery chance for two
reasons: their apparent magnitude is brighter than average and
they stay longer above the detection limit. But still, there are no
objects significantly above the Hubble line, not even at large
distances. This means: The sample of SNe Ia shown in Fig. 1
constitutes a homogeneous class of very luminous and unabsorbed
objects.
When in the following the calibration of Table 3 is applied to the SNe
Ia in Fig. 1, it should be kept in mind that Branch
normal SNe Ia (cf. Branch et al. 1993) are compared with the
most luminous SNe Ia known. Therefore the resulting value of  can only be, if anything, an upper limit.
can only be, if anything, an upper limit.
Forcing a slope of 5 (corresponding to linear expansion) to the
data in Fig. 1 gives
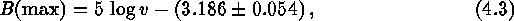
and

An easy calculation shows that the constant term  in equations (3) and (4) is determined by
in equations (3) and (4) is determined by
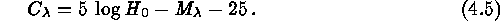
Inserting  and
and  from Table 5 leads directly to
from Table 5 leads directly to
 and
and 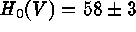 , from which we
adopt
, from which we
adopt
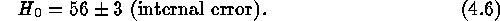
Equations (3) and (4) are defined out to  kms
kms .
The value of
.
The value of  therefore represents the truly cosmic expansion rate.
therefore represents the truly cosmic expansion rate.
At a time when only the very first calibrating SNe Ia were known, it was
suggested that SN 1972E was overluminous on the basis of its light curve
shape (Hamuy et al. 1995, Riess et al. 1995) and that consequently the true
value of 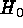 was larger. In the light of seven calibrators this
argument is now impossible. From first principles of stellar statistics,
it is known that seven nearby objects can on average not be more
luminous than a distant, luminosity-segregated sample.
was larger. In the light of seven calibrators this
argument is now impossible. From first principles of stellar statistics,
it is known that seven nearby objects can on average not be more
luminous than a distant, luminosity-segregated sample.
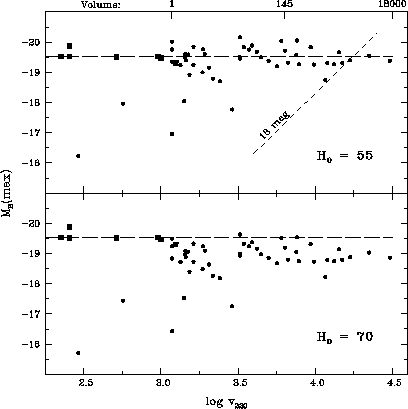
Figure: The absolute magnitude 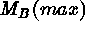 of all SNe Ia in or beyond
the Virgo cluster with known
of all SNe Ia in or beyond
the Virgo cluster with known 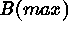 versus velocity distance. Also
shown are all faint red SNe Ia; they illustrate our point that
no underluminous (or absorbed) SNe Ia are found at large distances.
The distant objects must therefore be among the very brightest
ones.
versus velocity distance. Also
shown are all faint red SNe Ia; they illustrate our point that
no underluminous (or absorbed) SNe Ia are found at large distances.
The distant objects must therefore be among the very brightest
ones. 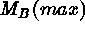 of the calibrators (squares) is based on their
Cepheid distances. For all other SNe Ia
of the calibrators (squares) is based on their
Cepheid distances. For all other SNe Ia 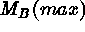 is calculated from
the recession velocities and
is calculated from
the recession velocities and 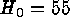 (upper panel) and
(upper panel) and 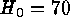 (lower panel). Note that for
(lower panel). Note that for 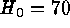 the impossible case arises
that the distant SNe Ia are on average less luminous than the nearby
calibrators.
the impossible case arises
that the distant SNe Ia are on average less luminous than the nearby
calibrators.
This point is illustrated in Fig. 2, where the absolute magnitudes of
the seven calibrators are compared to the absolute magnitudes of the
distant SN sample. The latter are calculated once with 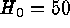 and
once with
and
once with  . For
. For 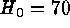 the absurd situation arises that the
distant SN Ia are systematically fainter than the nearby
calibrators. The firm conclusion from this is that
the absurd situation arises that the
distant SN Ia are systematically fainter than the nearby
calibrators. The firm conclusion from this is that  .
.
A more detailed discussion of all external errors is given elsewhere
(Tammann et al. 1996). It yields a confidence range of  .
.
The two independent routes towards the large-scale value of 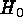 ,
via the Virgo cluster and SNe Ia, give 54
,
via the Virgo cluster and SNe Ia, give 54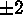 and 56
and 56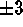 (internal errors), respectively. Their only interdependence is that
they rely on Cepheids (predominantly observed with HST), which are
the least controversial distance indicators at present. Together they
make a strong case for
(internal errors), respectively. Their only interdependence is that
they rely on Cepheids (predominantly observed with HST), which are
the least controversial distance indicators at present. Together they
make a strong case for 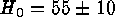 (external error). Values of
(external error). Values of
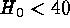 are equally unlikely as values of
are equally unlikely as values of 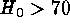 .
.
The relatively low value of 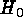 is supported by additional
methods, e.g., TF and other distances of field galaxies (Sandage 1994,
1996 and references therein), and the Zeldovich-Sunyaev effect
(Lasenby & Hancock 1995, Rephaeli 1995). Baum's et al. (1995) HST
photometry of globular clusters in the Coma cluster requires
is supported by additional
methods, e.g., TF and other distances of field galaxies (Sandage 1994,
1996 and references therein), and the Zeldovich-Sunyaev effect
(Lasenby & Hancock 1995, Rephaeli 1995). Baum's et al. (1995) HST
photometry of globular clusters in the Coma cluster requires
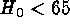 . A gravitationally lensed quasar sets
. A gravitationally lensed quasar sets  (Dahle
et al. 1994). Models of SNe Ia could not be understood if
(Dahle
et al. 1994). Models of SNe Ia could not be understood if  was
was
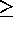 60 (Branch et al. 1996) or in no case
60 (Branch et al. 1996) or in no case 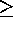 70 (Höflich &
Khokhlov 1996, Ruiz-Lapuente 1996).
70 (Höflich &
Khokhlov 1996, Ruiz-Lapuente 1996).
We believe that literature values significantly larger than 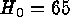 are explained by an unwarrantedly high Virgo velocity, the unrealistic
hope to fathom the depth of the Virgo cluster with only a single
galaxy, the myth of a sharp, dispersionless cutoff of the luminosity
function of planetary nebula shells, the reliance on the suspicious
surface brightness fluctuation method, and/or simply by Malmquist bias
which always artificially increases the value of
are explained by an unwarrantedly high Virgo velocity, the unrealistic
hope to fathom the depth of the Virgo cluster with only a single
galaxy, the myth of a sharp, dispersionless cutoff of the luminosity
function of planetary nebula shells, the reliance on the suspicious
surface brightness fluctuation method, and/or simply by Malmquist bias
which always artificially increases the value of  .
.
Acknowledgments:
The Basel group acknowledges the support of the Swiss National Science
Foundation. A.S. and A.S. thank NASA for its support for the overall  project. N.P. and F.D.M. acknowledge the support of ESA as part of its
ongoing commitment to the science done with HST. We are all grateful
to the people behind the scenes of HST, without whom none of the
observations used here would have been obtained.
project. N.P. and F.D.M. acknowledge the support of ESA as part of its
ongoing commitment to the science done with HST. We are all grateful
to the people behind the scenes of HST, without whom none of the
observations used here would have been obtained.
References:
Baum, W. A. et al. 1995, AJ, 110, 2537
Binggeli, B., Popescu, C. C., & Tammann, G. A. 1993, A&AS, 98, 275
Binggeli, B., Sandage, A., & Tammann, G. A. 1985, AJ, 90, 1681
Böhringer, H. et al. 1994, Nature, 368, 828
Bottinelli, L., Gougenheim, L., Paturel, G., & Teerkorpi, P.
1991, A&A, 252, 560
Branch, D., Fisher, A., & Nugent, P. 1993, AJ, 106, 2383
Branch, D., Nugent, P., & Fisher, A. 1996, in Thermonuclear
Supernovae, eds. R. Canal, P. Ruiz-Lapuente, & J. Isern (Dordrecht:
Kluwer Academic Publishers), in press
Burstein, D. & Heiles, C. 1984, ApJS, 54, 33
Capaccioli, M., Della Valle, M., D'Onofrio, M., & Rosino, L. A.
1989, AJ, 97, 1622
Ciardullo, R., Jacoby, G. H., & Ford, H. C. 1989, ApJ, 344, 715
Chiosi, C., Wood, P., & Capitanio, N. 1993, ApJS 86, 541
Cohen, J. G. 1985, ApJ, 292, 90
Dahle, H., Maddox, S. J., & Lilje, P. B. 1994, ApJ, 435, L79
Dressler, A. 1987, ApJ, 317, 1
Elson, R. A. W. & Santiago, B. X. 1996, MNRAS, in press
Faber, S. M. et al. 1989, ApJS, 69, 763
Feast, M. & Walker, A. R. 1987, ARA&A, 25, 345
Federspiel, M., Tammann, G. A., & Sandage, A. 1996, in press.
Freedman, W. L. & Madore, B. F. 1990, ApJ, 365, 186
Freedman, W. L. & Madore, B. F. 1994, ApJ, 427, 628
Freedman, W. L. et al. 1994, Nature 371, 757
Fritze-von Alvensleben, U. 1995, private communication
Gould, A. 1994, ApJ, 425, 51
Hamuy, M. et al. 1995, AJ, 109, 1
Harris, W. E. 1990, PASP, 102, 966
Höflich, P. & Khokhlov, A. 1996, ApJ, 457, 500
Höflich, P., Khokhlov, A., Wheeler, J.C., Nomoto, K., &
Thielemann, F.K. 1996, in Thermonuclear Supernovae, eds. R. Canal,
P. Ruiz-Lapuente, & J. Isern (Dordrecht: Kluwer Academic Publishers),
in press
Huchra, J. 1988, in The Extragalactic Distance Scale, eds.
S. van den Bergh & C. J. Pritchet, (San Francisco: Astronomical Society
of the Pacific), 257
Jacoby, G. H., Ciardullo, R. 1993, in Planetary Nebulae,
eds. R. Weinberger & A. Acker, (IAU Symposium 155), 503
Jacoby, G. H., Ciardullo, R., Booth, J., & Ford, H. C. 1989,
ApJ, 344, 704
Jacoby, G. H., Ciardullo, R., & Ford, H. C. 1990, ApJ, 356, 332
Jerjen, H. 1995, private communication
Jerjen, H. & Tammann, G. A. 1993, A&A, 276, 1
Kelson, D. 1995, private communication
Kennicutt, R. C., Freedman, W. L., & Mould, J. R. 1995,
AJ, 110, 1476
Kraan-Korteweg, R. C. 1986, A&AS, 66, 255
Lasenby, A. N. & Hancock, S. 1995, in Current Topics in
Astrofundamental Physics: The Early Universe, eds. N. Sanchez &
A. Zichichi, (Dordrecht: Kluwer Academic Publishers), 327
Lorenz, H., Böhm, P., Capaccioli, M., Richter, G. M., & Longo,
G. 1993, A&A, 277, L15
Madore, B.F. & Freedman, W. L. 1991, PASP, 103, 933
Méndez, R. H., Kudritzki, R. P., Ciardullo, R., & Jacoby, G. H.
1993, A&A, 275, 534
Mould, J. R. et al. 1995, ApJ, 449, 413
Panagia, N., Gilmozzi, R., Macchetto, F. D., Adorf, H.-M., &
Kirshner, R. P. 1991, ApJ, 380, L23
Phillips, M. M. 1993, ApJ, 413, L105
Phillips, M. M., Jacoby, G. H., Walker, A. R., Tonry, J. L., &
Ciardullo, R. 1992, BAAS, 24, 749
Pritchet, C. J. & van den Bergh, S. 1987, ApJ, 318, 507
Rephaeli, Y. 1995, ARA&A, 33, 541
Riess, A. G., Press, W. H., & Kirshner, R. P. 1995, ApJ, 438, L17
Ruiz-Lapuente, P. 1996, preprint
Saha, A., Labhardt, L., Schwengeler, H., Macchetto, F. D.,
Panagia, N., Sandage, A., & Tammann, G. A. 1994, ApJ, 425, 14 (IC 4182)
Saha, A., Sandage, A., Labhardt, L., Schwengeler, H.,
Tammann, G. A., Panagia, N., & Macchetto, F. D. 1995, ApJ, 438, 8 (NGC 5253)
Saha, A., Sandage, A., Labhardt, L., Tammann, G. A.,
Macchetto, F. D., & Panagia, N. 1996a, ApJ, in press (NGC 4536)
Saha, A., Sandage, A., Labhardt, L., Tammann, G. A.,
Macchetto, F. D., & Panagia, N. 1996b, ApJ, in press (NGC 4496A)
Sandage, A. 1988, PASP, 100, 935
Sandage, A. 1994, ApJ, 430, 1
Sandage, A. 1996, AJ, 111, 1 and 18
Sandage, A. & Bedke, J. 1994, Atlas of Galaxies (Washington, D.C.:
NASA)
Sandage, A., Saha, A., Tammann, G. A., Labhardt, L., Panagia, N.,
& Macchetto, F. D. 1996, ApJ, in press
Sandage, A., Saha, A., Tammann, G. A., Labhardt, L.,
Schwengeler, H., Panagia, N., & Macchetto, F. D. 1994, ApJ, 423, L13
(NGC 5253)
Sandage, A., Saha, A., Tammann, G. A., Panagia, N., &
Macchetto, F. D. 1992, ApJ, 401, L7 (IC 4182)
Sandage, A. & Tammann, G. A. 1968, ApJ, 151, 531
Sandage, A. & Tammann, G. A. 1974, ApJ, 194, 223
Sandage, A. & Tammann, G. A. 1990, ApJ, 365, 1
Sandage, A. & Tammann, G. A. 1995, ApJ, 446, 1
Sandage, A. & Tammann, G. A. 1996, ApJ, in press
Schaefer, B.E. 1995, ApJ, 447, L13
Schröder, A. C. 1995, Ph.D. Thesis, Univ. Basel
Soffner, T. et al. 1995, A&A, in press
Tanvir, N. R., Shanks, T., Ferguson, H. C., & Robinson, D. R. T.
1995, Nature, 377, 27
Tammann, G. A. 1988, in The Extragalactic Distance Scale, eds.
S. van den Bergh & C. J. Pritchet, (San Francisco: Astronomical Society
of the Pacific), 282
Tammann, G. A. 1993, in Planetary Nebulae, eds. R. Weinberger &
A. Acker, (IAU Symposium 155), 515
Tammann, G. A. & Sandage, A. 1968, ApJ, 151, 825
Tammann, G. A. & Sandage, A. 1995, ApJ, 452, 16
Tammann, G. A. Sandage, A., Saha, A., Labhardt, L.,
Macchetto, F. D., & Panagia, N. 1996, in Thermonuclear Supernovae,
eds. R. Canal, P. Ruiz-Lapuente, & J. Isern (Dordrecht: Kluwer
Academic Publishers), in press
Tonry, J. L. 1991, ApJ, 373, L1
Tonry, J. L., Ajhar, E. A., & Luppino, G. A. 1990, AJ, 100,1416
Tonry, J. L. & Schneider, D. P. 1988, AJ, 96, 807
Whitmore, B. C. et al. 1995, ApJ, 454, 773





Next: Distant Galaxies
Up: HST and the
Previous: The HST Key
payne@stsci.edu
 is already
enormous and it can only grow. In Table 1 a compilation is given of
distance determinations with HST having some bearing on
is already
enormous and it can only grow. In Table 1 a compilation is given of
distance determinations with HST having some bearing on 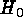 . The
values scatter between 55 and 80 and the formal mean is
. The
values scatter between 55 and 80 and the formal mean is 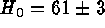 .
This, however, is not the best value, because some values shown are
mutually incompatible.
.
This, however, is not the best value, because some values shown are
mutually incompatible.
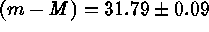 . Other distance
indicators support this value. The adopted linear distance of
. Other distance
indicators support this value. The adopted linear distance of  Mpc combined with the cluster velocity of
Mpc combined with the cluster velocity of  (in the CMB frame) gives
(in the CMB frame) gives  (internal error). (2) Six of the
galaxies have been the site of seven SNe Ia with well observed maxima. Their
resulting calibration in absolute magnitudes gives
(internal error). (2) Six of the
galaxies have been the site of seven SNe Ia with well observed maxima. Their
resulting calibration in absolute magnitudes gives 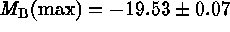 and
and 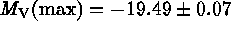 with
negligible intrinsic scatter. If this calibration is used to
determine the distances of all distant SNe Ia with known maxima and
with
with
negligible intrinsic scatter. If this calibration is used to
determine the distances of all distant SNe Ia with known maxima and
with 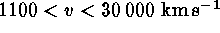 ,
, 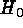 becomes
becomes 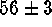 (internal error). Systematic errors tend to make this an upper limit; in
particular, the case
(internal error). Systematic errors tend to make this an upper limit; in
particular, the case 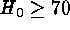 can be excluded.---The conclusion is that
the large-scale value of the Hubble constant is
can be excluded.---The conclusion is that
the large-scale value of the Hubble constant is 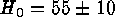 (external
error).
(external
error).
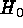 to which HST has
heavily contributed. The first route via the Virgo cluster is
described in Section 2, the second route using supernovae of type Ia
(SNe Ia) is discussed in Section 3.
to which HST has
heavily contributed. The first route via the Virgo cluster is
described in Section 2, the second route using supernovae of type Ia
(SNe Ia) is discussed in Section 3.

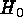 determinations from HST
determinations from HST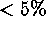 in linear distance. The slope
of the relation is well determined by the LMC Cepheids; it is of less
importance as long as the Cepheids under consideration cover a
sufficient period range, which is also needed to avoid selection
effects (Sandage 1988). Metallicity effects are believed to be small
(Freedman & Madore 1990, Chiosi et al. 1993).
in linear distance. The slope
of the relation is well determined by the LMC Cepheids; it is of less
importance as long as the Cepheids under consideration cover a
sufficient period range, which is also needed to avoid selection
effects (Sandage 1988). Metallicity effects are believed to be small
(Freedman & Madore 1990, Chiosi et al. 1993).
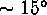 in the sky!). Its distance is 25 Mpc
(Sandage et al. 1996) and yet it is a bona fide cluster member; with a
small velocity of 800 kms
in the sky!). Its distance is 25 Mpc
(Sandage et al. 1996) and yet it is a bona fide cluster member; with a
small velocity of 800 kms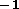 , it cannot be assigned to the
background.
, it cannot be assigned to the
background.
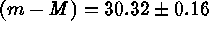 out to the
Virgo cluster by means of relative distance determinations. The
best available relative distances are compiled in Table 2. Adding the
mean difference of
out to the
Virgo cluster by means of relative distance determinations. The
best available relative distances are compiled in Table 2. Adding the
mean difference of  to the above distance
modulus gives a Virgo cluster modulus of
to the above distance
modulus gives a Virgo cluster modulus of 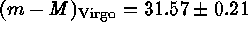 .
For brevity we will refer to this value in the following as the
Cepheid distance of the Virgo cluster .
.
For brevity we will refer to this value in the following as the
Cepheid distance of the Virgo cluster .

 (w= inclination-corrected 21cm-line
width). Two close companions of M101 bring the number of useful calibrators
to 13 (cf. Table 3). Two galaxies (M101 and M100) are less inclined than
the frequently adopted limit of
(w= inclination-corrected 21cm-line
width). Two close companions of M101 bring the number of useful calibrators
to 13 (cf. Table 3). Two galaxies (M101 and M100) are less inclined than
the frequently adopted limit of 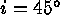 ; yet their inclinations are
so well defined by mapping their velocity field that they are still useful
as calibrators.
; yet their inclinations are
so well defined by mapping their velocity field that they are still useful
as calibrators.

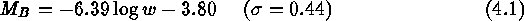
 and
lying within the isopleths of substructures A and B (see Binggeli et
al. 1993) or, without changing the result, within the X-ray contour of
the cluster (Böhringer et al. 1994). This sample together with
equation (1) gives
and
lying within the isopleths of substructures A and B (see Binggeli et
al. 1993) or, without changing the result, within the X-ray contour of
the cluster (Böhringer et al. 1994). This sample together with
equation (1) gives 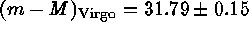 . The use of infrared
instead of B magnitudes does not bring an advantage (Schröder
1995), nor does the application of the inverse TF relation. For
the robustness of the result against variations of the input
parameters the reader is referred to Federspiel et al. (1996).
. The use of infrared
instead of B magnitudes does not bring an advantage (Schröder
1995), nor does the application of the inverse TF relation. For
the robustness of the result against variations of the input
parameters the reader is referred to Federspiel et al. (1996).
 (Sandage & Tammann
1995). Meanwhile Whitmore et al. (1995) found a very bright peak
magnitude in V and I for NGC 4486, which is well determined with
HST and which corresponds, with our precepts, to a modulus of
(Sandage & Tammann
1995). Meanwhile Whitmore et al. (1995) found a very bright peak
magnitude in V and I for NGC 4486, which is well determined with
HST and which corresponds, with our precepts, to a modulus of
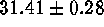 (Sandage & Tammann 1996). However, the GCs in
NGC 4486 have a bimodal color distribution which is suggestive of age
differences and possible merger effects (Fritze-von Alvensleben 1995,
Elson & Santiago 1996). Turning a blind eye to this problem and
averaging over all available GCLFs in Virgo we obtain
(Sandage & Tammann 1996). However, the GCs in
NGC 4486 have a bimodal color distribution which is suggestive of age
differences and possible merger effects (Fritze-von Alvensleben 1995,
Elson & Santiago 1996). Turning a blind eye to this problem and
averaging over all available GCLFs in Virgo we obtain
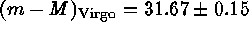 . We are aware that the method may still
face considerable problems.
. We are aware that the method may still
face considerable problems.
 method, normally applied to ellipticals, was extended
to the bulges of S0 and spiral galaxies by Dressler (1987). Using the bulges
of the Galaxy, M31, and M81 as local calibrators, one obtains
method, normally applied to ellipticals, was extended
to the bulges of S0 and spiral galaxies by Dressler (1987). Using the bulges
of the Galaxy, M31, and M81 as local calibrators, one obtains 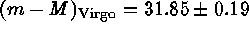 (Tammann 1988).
(Tammann 1988).
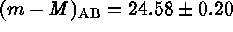 (i.e., somewhat less than indicated by Cepheids). From six novae in
three Virgo ellipticals Pritchet & van den Bergh (1987) concluded
that the cluster is more distant by
(i.e., somewhat less than indicated by Cepheids). From six novae in
three Virgo ellipticals Pritchet & van den Bergh (1987) concluded
that the cluster is more distant by 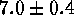 mag than the apparent
modulus of M31, implying
mag than the apparent
modulus of M31, implying 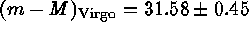 (zero
absorption is adopted for the Virgo cluster, see Section 2.6). The
result carries still small weight, but is interesting because it is
based on novae exclusively. HST observations, although
time-consuming, of novae in the Virgo cluster could much improve this
independent result.
(zero
absorption is adopted for the Virgo cluster, see Section 2.6). The
result carries still small weight, but is interesting because it is
based on novae exclusively. HST observations, although
time-consuming, of novae in the Virgo cluster could much improve this
independent result.
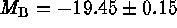 for ``Branch normal'' objects (Branch 1996,
Höflich & Khokhlov 1996, Ruiz-Lapuente 1996). It is true that fainter,
nearby SNe Ia are known, but being red and spectroscopically peculiar they
can easily be singled out, and they do not contaminate distant,
luminosity-selected samples of SNe Ia (cf. Section 3). Eight SNe Ia which
have occurred in the Virgo cluster have
for ``Branch normal'' objects (Branch 1996,
Höflich & Khokhlov 1996, Ruiz-Lapuente 1996). It is true that fainter,
nearby SNe Ia are known, but being red and spectroscopically peculiar they
can easily be singled out, and they do not contaminate distant,
luminosity-selected samples of SNe Ia (cf. Section 3). Eight SNe Ia which
have occurred in the Virgo cluster have 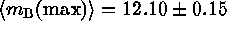 mag. This value combined with the theoretical calibration
gives
mag. This value combined with the theoretical calibration
gives 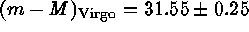 .---Had we used instead the
empirical calibration of Table 5 below, the Virgo modulus would have become
larger by 0.08 mag. We refrain from using this value because the routes
towards
.---Had we used instead the
empirical calibration of Table 5 below, the Virgo modulus would have become
larger by 0.08 mag. We refrain from using this value because the routes
towards 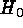 in Sections 2 and 3 are to be kept strictly apart.
in Sections 2 and 3 are to be kept strictly apart.
 mag has led to a Virgo modulus significantly lower
than obtained from the six methods discussed above (Jacoby et
al. 1990). Yet it was pointed out that the cutoff magnitude depends
on the sample size (i.e., the absolute magnitude of the parent galaxy;
Bottinelli et al. 1991, Tammann 1993). Numerically simulated LFs of
the shell luminosities confirm, indeed, the dependence on sample size
and population age (Méndez et al. 1993). As a consequence, the
published PN distances deviate systematically from the Cepheid
distances. The deviations increase with distance from M81 (Jacoby
et al. 1989), NGC 5253 (Jacoby & Ciardullo 1993), and the Leo
group (Ciardullo et al. 1989) to reach at the Virgo cluster
(Jacoby et al. 1990) 0.74 mag !---A new method to derive PN
distances, allowing for sample size and other effects, has been
proposed by Soffner et al. (1995); the first result for the nearby
galaxy NGC 300 is encouraging.
mag has led to a Virgo modulus significantly lower
than obtained from the six methods discussed above (Jacoby et
al. 1990). Yet it was pointed out that the cutoff magnitude depends
on the sample size (i.e., the absolute magnitude of the parent galaxy;
Bottinelli et al. 1991, Tammann 1993). Numerically simulated LFs of
the shell luminosities confirm, indeed, the dependence on sample size
and population age (Méndez et al. 1993). As a consequence, the
published PN distances deviate systematically from the Cepheid
distances. The deviations increase with distance from M81 (Jacoby
et al. 1989), NGC 5253 (Jacoby & Ciardullo 1993), and the Leo
group (Ciardullo et al. 1989) to reach at the Virgo cluster
(Jacoby et al. 1990) 0.74 mag !---A new method to derive PN
distances, allowing for sample size and other effects, has been
proposed by Soffner et al. (1995); the first result for the nearby
galaxy NGC 300 is encouraging.
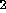 index
(Lorenz et al. 1993). Finally, we note that the SBF distances of
NGC 5253 (Phillips et al. 1992), the Leo group (Tonry 1991), and the
Virgo cluster (Tonry 1991) are smaller than Cepheid distances by as
much as 0.97, 0.48, and 0.56 mag, respectively.
index
(Lorenz et al. 1993). Finally, we note that the SBF distances of
NGC 5253 (Phillips et al. 1992), the Leo group (Tonry 1991), and the
Virgo cluster (Tonry 1991) are smaller than Cepheid distances by as
much as 0.97, 0.48, and 0.56 mag, respectively.
 (with respect to the Local Group
centroid). If one considers instead the 361 galaxies within the very
similar X-ray contour of the cluster (Böhringer et al. 1994), the mean
velocity becomes
(with respect to the Local Group
centroid). If one considers instead the 361 galaxies within the very
similar X-ray contour of the cluster (Böhringer et al. 1994), the mean
velocity becomes 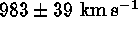 . Taking all 385 galaxies
with redshifts in the Virgo survey area, excluding only background objects,
we find
. Taking all 385 galaxies
with redshifts in the Virgo survey area, excluding only background objects,
we find 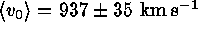 . From this we
adopt a best cluster velocity of
. From this we
adopt a best cluster velocity of 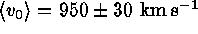 . This result supersedes an early value of
. This result supersedes an early value of  (Huchra 1988) which was based on only 250
galaxies and a less well defined area.
(Huchra 1988) which was based on only 250
galaxies and a less well defined area.
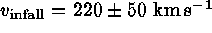 (cf. Tammann
1996) and find for Virgo
(cf. Tammann
1996) and find for Virgo 
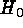 at the distance of Coma. One can repeat that with any cluster whose
distance relative to Virgo is known. In fact there are at least 14 clusters
with rather good relative distances and velocities
at the distance of Coma. One can repeat that with any cluster whose
distance relative to Virgo is known. In fact there are at least 14 clusters
with rather good relative distances and velocities  (
( is the velocity in the frame
of the microwave background). The best cosmic value of
is the velocity in the frame
of the microwave background). The best cosmic value of  is then the
all-sky mean over 14 different
is then the
all-sky mean over 14 different  determinations. But more elegant is
the reverse method: the relative distances are used to scale down the
velocities of the 14 clusters and to predict a mean Virgo cluster velocity,
i.e., the
determinations. But more elegant is
the reverse method: the relative distances are used to scale down the
velocities of the 14 clusters and to predict a mean Virgo cluster velocity,
i.e., the 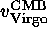 velocity which the cluster would have in
the absence of all local deviations from an ideal expansion field. The
result of this procedure is
velocity which the cluster would have in
the absence of all local deviations from an ideal expansion field. The
result of this procedure is 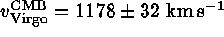 (Sandage & Tammann 1990, Jerjen & Tammann 1993, Jerjen 1995
for a more rigid error determination).
(Sandage & Tammann 1990, Jerjen & Tammann 1993, Jerjen 1995
for a more rigid error determination).

 Mpc is combined with
Mpc is combined with
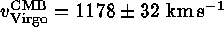 one obtains
one obtains

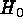 . The aim is to derive Cepheid distances (in V and I to
control absorption effects) of up to ten galaxies which have produced
well observed SNe Ia. So far we have calibrated the peak luminosity of
six SNe Ia. A seventh object has become available through Tanvir's et
al. (1995) Cepheid distance of the Leo group. (It can be assumed that
the member galaxies of this compact group lie practically at the same
distance.) The resulting absolute magnitudes of the seven SNe Ia are
shown in Table 5. Detailed discussions of the input parameters are
given elsewhere (Sandage et al. 1996, Tammann et al. 1996;
negligible differences between these sources are due to a different
weighting of individual sources). The agreement to within the errors
between the individual luminosities supports the claim that SNe Ia are
(nearly) perfect standard candles. Independent confirmation of the
luminosities comes from Höflich et al. (1996) who have three SNe Ia
in common with Table 5. Their model luminosities are the same
to within
. The aim is to derive Cepheid distances (in V and I to
control absorption effects) of up to ten galaxies which have produced
well observed SNe Ia. So far we have calibrated the peak luminosity of
six SNe Ia. A seventh object has become available through Tanvir's et
al. (1995) Cepheid distance of the Leo group. (It can be assumed that
the member galaxies of this compact group lie practically at the same
distance.) The resulting absolute magnitudes of the seven SNe Ia are
shown in Table 5. Detailed discussions of the input parameters are
given elsewhere (Sandage et al. 1996, Tammann et al. 1996;
negligible differences between these sources are due to a different
weighting of individual sources). The agreement to within the errors
between the individual luminosities supports the claim that SNe Ia are
(nearly) perfect standard candles. Independent confirmation of the
luminosities comes from Höflich et al. (1996) who have three SNe Ia
in common with Table 5. Their model luminosities are the same
to within 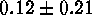 mag. Branch's (1996) model luminosity of SN
1981B agrees fortuitously well with ours, and two SNe Ia of
Ruiz-Lapuente (1996) are fainter by only
mag. Branch's (1996) model luminosity of SN
1981B agrees fortuitously well with ours, and two SNe Ia of
Ruiz-Lapuente (1996) are fainter by only  mag judging
from their late spectra and the inferred
mag judging
from their late spectra and the inferred  Ni mass.
Ni mass.


 with
reasonably well determined maximum magnitudes is shown in Fig. 1
(Tammann & Sandage 1995). Their intrinsic luminosity scatter
must be considerably less than 0.35 mag, because much of the scatter
is expected from observational errors and peculiar motions. Indeed, the
intrinsic scatter must be very small because even the most distant SNe
Ia lie very close to the theoretical Hubble line of slope 0.2. The
argument goes as follows. The most distant SNe Ia occupy a volume
about 18000 times larger than that of the local calibrators. The
large volume must contain exceptionally luminous SNe Ia---if they
existed---and they have a much enhanced discovery chance for two
reasons: their apparent magnitude is brighter than average and
they stay longer above the detection limit. But still, there are no
objects significantly above the Hubble line, not even at large
distances. This means: The sample of SNe Ia shown in Fig. 1
constitutes a homogeneous class of very luminous and unabsorbed
objects.
with
reasonably well determined maximum magnitudes is shown in Fig. 1
(Tammann & Sandage 1995). Their intrinsic luminosity scatter
must be considerably less than 0.35 mag, because much of the scatter
is expected from observational errors and peculiar motions. Indeed, the
intrinsic scatter must be very small because even the most distant SNe
Ia lie very close to the theoretical Hubble line of slope 0.2. The
argument goes as follows. The most distant SNe Ia occupy a volume
about 18000 times larger than that of the local calibrators. The
large volume must contain exceptionally luminous SNe Ia---if they
existed---and they have a much enhanced discovery chance for two
reasons: their apparent magnitude is brighter than average and
they stay longer above the detection limit. But still, there are no
objects significantly above the Hubble line, not even at large
distances. This means: The sample of SNe Ia shown in Fig. 1
constitutes a homogeneous class of very luminous and unabsorbed
objects.
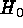 can only be, if anything, an upper limit.
can only be, if anything, an upper limit.
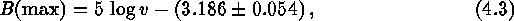

 in equations (3) and (4) is determined by
in equations (3) and (4) is determined by
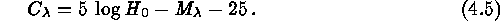
 and
and  from Table 5 leads directly to
from Table 5 leads directly to
 and
and 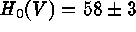 , from which we
adopt
, from which we
adopt
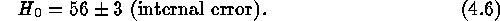
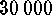 kms
kms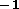 .
The value of
.
The value of  therefore represents the truly cosmic expansion rate.
therefore represents the truly cosmic expansion rate.
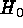 was larger. In the light of seven calibrators this
argument is now impossible. From first principles of stellar statistics,
it is known that seven nearby objects can on average not be more
luminous than a distant, luminosity-segregated sample.
was larger. In the light of seven calibrators this
argument is now impossible. From first principles of stellar statistics,
it is known that seven nearby objects can on average not be more
luminous than a distant, luminosity-segregated sample.

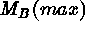 of all SNe Ia in or beyond
the Virgo cluster with known
of all SNe Ia in or beyond
the Virgo cluster with known 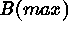 versus velocity distance. Also
shown are all faint red SNe Ia; they illustrate our point that
no underluminous (or absorbed) SNe Ia are found at large distances.
The distant objects must therefore be among the very brightest
ones.
versus velocity distance. Also
shown are all faint red SNe Ia; they illustrate our point that
no underluminous (or absorbed) SNe Ia are found at large distances.
The distant objects must therefore be among the very brightest
ones. 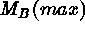 of the calibrators (squares) is based on their
Cepheid distances. For all other SNe Ia
of the calibrators (squares) is based on their
Cepheid distances. For all other SNe Ia 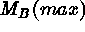 is calculated from
the recession velocities and
is calculated from
the recession velocities and 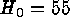 (upper panel) and
(upper panel) and 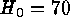 (lower panel). Note that for
(lower panel). Note that for 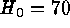 the impossible case arises
that the distant SNe Ia are on average less luminous than the nearby
calibrators.
the impossible case arises
that the distant SNe Ia are on average less luminous than the nearby
calibrators.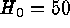 and
once with
and
once with  . For
. For 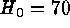 the absurd situation arises that the
distant SN Ia are systematically fainter than the nearby
calibrators. The firm conclusion from this is that
the absurd situation arises that the
distant SN Ia are systematically fainter than the nearby
calibrators. The firm conclusion from this is that  .
.
 .
.
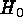 ,
via the Virgo cluster and SNe Ia, give 54
,
via the Virgo cluster and SNe Ia, give 54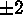 and 56
and 56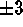 (internal errors), respectively. Their only interdependence is that
they rely on Cepheids (predominantly observed with HST), which are
the least controversial distance indicators at present. Together they
make a strong case for
(internal errors), respectively. Their only interdependence is that
they rely on Cepheids (predominantly observed with HST), which are
the least controversial distance indicators at present. Together they
make a strong case for 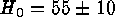 (external error). Values of
(external error). Values of
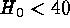 are equally unlikely as values of
are equally unlikely as values of 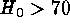 .
.
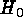 is supported by additional
methods, e.g., TF and other distances of field galaxies (Sandage 1994,
1996 and references therein), and the Zeldovich-Sunyaev effect
(Lasenby & Hancock 1995, Rephaeli 1995). Baum's et al. (1995) HST
photometry of globular clusters in the Coma cluster requires
is supported by additional
methods, e.g., TF and other distances of field galaxies (Sandage 1994,
1996 and references therein), and the Zeldovich-Sunyaev effect
(Lasenby & Hancock 1995, Rephaeli 1995). Baum's et al. (1995) HST
photometry of globular clusters in the Coma cluster requires
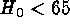 . A gravitationally lensed quasar sets
. A gravitationally lensed quasar sets  (Dahle
et al. 1994). Models of SNe Ia could not be understood if
(Dahle
et al. 1994). Models of SNe Ia could not be understood if  was
was
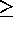 60 (Branch et al. 1996) or in no case
60 (Branch et al. 1996) or in no case 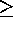 70 (Höflich &
Khokhlov 1996, Ruiz-Lapuente 1996).
70 (Höflich &
Khokhlov 1996, Ruiz-Lapuente 1996).
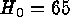 are explained by an unwarrantedly high Virgo velocity, the unrealistic
hope to fathom the depth of the Virgo cluster with only a single
galaxy, the myth of a sharp, dispersionless cutoff of the luminosity
function of planetary nebula shells, the reliance on the suspicious
surface brightness fluctuation method, and/or simply by Malmquist bias
which always artificially increases the value of
are explained by an unwarrantedly high Virgo velocity, the unrealistic
hope to fathom the depth of the Virgo cluster with only a single
galaxy, the myth of a sharp, dispersionless cutoff of the luminosity
function of planetary nebula shells, the reliance on the suspicious
surface brightness fluctuation method, and/or simply by Malmquist bias
which always artificially increases the value of  .
.
 project. N.P. and F.D.M. acknowledge the support of ESA as part of its
ongoing commitment to the science done with HST. We are all grateful
to the people behind the scenes of HST, without whom none of the
observations used here would have been obtained.
project. N.P. and F.D.M. acknowledge the support of ESA as part of its
ongoing commitment to the science done with HST. We are all grateful
to the people behind the scenes of HST, without whom none of the
observations used here would have been obtained.