Глава VII. Анализ размерностей и численное моделирование звездных систем
Теория анализа размерностей и подобия может применяться и в звездной астрономии, занимающейся изучением динамики звездных систем. Некоторые задачи на применение методов анализа размерностей к звездным системам были рассмотрены в гл. 2. Здесь мы более подробно рассмотрим методы анализа размерностей и особенно численное моделирование применительно к звездным системам, рассматриваемым как скопление материальных точек, движущихся под действием взаимного гравитационного притяжения. Столкновениями звезд будем пренебрегать. Как и в предыдущих главах, мы не претендуем на полное изложение теории звездных систем, основное внимание уделено вопросам анализа размерностей и численному моделированию.
§ 7.1 Система уравнений и параметры звездных систем
Термином "звездная система" можно обозначать скопления звезд с самым различным их числом - от нескольких звезд в кратных системах до галактик с сотнями миллиардов звезд. К звездным системам можно отнести и скопления галактик. Общим для всех этих систем является то, что их строение и эволюция определяются только силами взаимного гравитационного притяжения. Основная система уравнений, описывающая такие объекты, есть
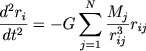
|
(7.1) |
Здесь ri - радиус вектор i звезды (или галактики), Mi - ее масса, rij=ri-rj, N - число звезд или галактик в системе. Анализом следствий, вытекающих из уравнений (7.1), и методов их численного решения мы и будем заниматься.
Для этого нам будет удобнее все многообразие звездных систем разбить на две основные группы:
1. Звездные системы, состоящие из относительно небольшого числа звезд (N ≈ 10-105). К ним относятся галактические скопления и скопления галактик. Форма таких систем более или менее сферична, заметного вращения у них нет. Впредь мы будем называть такие системы просто скоплениями, считать их сферичными и предполагать,что они не вращаются.
2. 1.Спиральные галактики, показывающие очень уплощенную структуру (толщина в 10-20 раз меньше диаметра). Такие системы быстро вращаются, но само вращение неоднородно (нетвердотельно). Число звезд в спиральных галактиках N ≈ 1010-1012. В дальнейшем такие системы, которые мы будем называть просто галактиками, будут считаться очень плоскими и быстро вращающимися, так что их структура в первую очередь определяется именно условиями вращения.
Разумеется, этими двумя группами отнюдь не исчерпывается разнообразие звездных систем. Есть эллиптические галактики, в том числе и сферической формы, без заметного вращения, но имеющие 1010 и более звезд. Очень разнообразны геометрические формы галактических скоплений. Известны случаи систем негравитационно взаимодействующих галактик. Даже сильно уплощенные спиральные галактики состоят из подсистем, в число которых входят промежуточные и сферические подсистемы. Разумеется, все эти особенности также нуждаются в теоретической интерпретации.
Однако, еще раз подчеркиваем, с точки зрения исследования общих свойств звездных систем на основе теории анализа размерностей и подобия и для постановки численного моделирования звездных систем достаточно рассмотреть два их типа - квазисферические невращаюшиеся системы с относительно небольшим числом звезд и быстро вращающиеся плоские галактики с очень большим числом звезд.
Звездные системы мы будем характеризовать их полной массой
|
|
(7.2) |
где ![]() - средняя масса звезды. Строго говоря, динамика звездных систем зависит и от распределения звезд по массам. Пусть f(M)dM - нормированное на N число звезд в скоплении с массами от M до M+dM. Тогда
- средняя масса звезды. Строго говоря, динамика звездных систем зависит и от распределения звезд по массам. Пусть f(M)dM - нормированное на N число звезд в скоплении с массами от M до M+dM. Тогда
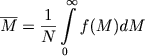
|
(7.3) |
Во многих случаях мы не будем учитывать различие масс звезд. Тогда мы будем считать все звезды имеющими одинаковую массу ![]() . Но в некоторых задачах учет функции f(M) обязателен. Вторым важным параметром является радиус системы R. Пространственное распределение звезд в звездных системах, как правило, неоднородно. Часто имеет место концентрация звезд к центру. Тем не менее можно вести среднюю концентрацию звезд - объемную (среднее число звезд в единице объема) для скоплений и поверхностную (среднее число звезд на единицу поверхности) в галактиках. Имеем для средней объемной концентрации
. Но в некоторых задачах учет функции f(M) обязателен. Вторым важным параметром является радиус системы R. Пространственное распределение звезд в звездных системах, как правило, неоднородно. Часто имеет место концентрация звезд к центру. Тем не менее можно вести среднюю концентрацию звезд - объемную (среднее число звезд в единице объема) для скоплений и поверхностную (среднее число звезд на единицу поверхности) в галактиках. Имеем для средней объемной концентрации
|
|
(7.4) |
и для средней поверхностной концентрации
|
|
(7.5) |
Также не однородно и вращение галактик, и здесь можно ввести параметр ![]() - среднюю угловую скорость вращения. В невращающихся звездных системах параметра Ω нет, но удобно ввести параметр характерного времени пересечения одной звездой всего скопления, обозначаемый в дальнейшем через P. Добавляя ко всем размерным параметрам и безразмерный параметр N - число звезд в скоплении, имеем следующие наборы характерных параметров звездных систем:
- среднюю угловую скорость вращения. В невращающихся звездных системах параметра Ω нет, но удобно ввести параметр характерного времени пересечения одной звездой всего скопления, обозначаемый в дальнейшем через P. Добавляя ко всем размерным параметрам и безразмерный параметр N - число звезд в скоплении, имеем следующие наборы характерных параметров звездных систем:
1. Скопления
|
|
(7.6) |
2. Галактики
|
|
(7.7) |
Здесь только ![]() и
и ![]() могут быть выражены через комбинации других параметров.
могут быть выражены через комбинации других параметров.
Из комбинаций независимых размерных параметров (7.6) и (7.7) могут быть составлены только по одному безразмерному комплексу. Имеем матрицу размерности для скоплений:
![$$
\begin{matrix}
\, & [G] & [\mathcal{M}] & [R] & [P] \\
\mbox{г}&-1&1&0&0 \\
\mbox{см}&3&0&1&0 \\
\mbox{сек}&-2&0&0&1
\end{matrix}
$$](http://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula206.gif)
|
Отсюда следует безразмерный комплекс
|
|
(7.8) |
Матрица размерности для галактик имеет вид
![$$
\begin{matrix}
\, & [G] & [\mathcal{M}] & [R] & [\Omega] \\
\mbox{г} & -1 & 1 & 0 & 0 \\
\mbox{см} & 3 & 0 & 1 & 0 \\
\mbox{сек}&-2 & 0 & 0 & -1
\end{matrix}
$$](http://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula208.gif)
|
Ей соответствует безразмерный комплекс
|
|
(7.9) |
Как обычно, численные значения безразмерных комплексов методами теории размерности не определяются, но из того факта, что имеется лишь по одному безразмерному комплексу, следует, что в первом приближении величины Π должны быть порядка единицы. Строго говоря, безразмерные комплексы Π, определенные формулами (7.8) и (7.9), должны в первую очередь зависеть от геометрии системы и лишь существенно слабее от числа звезд в этой системе. Чтобы в этом убедиться, используем методы теории подобия.
Введем в (7.1) безразмерные переменные посредством замены
|
|
(7.10) |
а также
|
|
(7.11) |
для скоплений галактик или галактик соответственно. Тогда система (7.1) приобретет вид
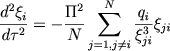
|
(7.12) |
где ξji = ξj - ξi. Число членов в правых частях каждого из уравнений системы (7.12) равно N-1. Поэтому рассматривать подобные по структуре (например, с одинаковой концентрацией к центру сферические скопления), но состоящие из разного числа звезд системы, то правые части уравнений (7.12) приближенно равны параметру Π2, умноженному на среднее значение безразмерной величины qi/ξji2, которое лишь в слабой степени зависит от полного числа звезд в скоплении.
Таким образом, ограничиваясь двумя классами звездных систем - квазиcферичеекими невращающимися звездными скоплениями и плоскими вращающимися галактиками - и предполагая их геометрическое подобие, мы можем считать, что независимо от числа звезд в системе безразмерные комплексы Π должны быть одинаковыми для каждого класса систем. По смыслу определения безразмерных переменных (7.10) и (7.11) величины qi, ξi и τ должны быть порядка единицы. Поэтому и безразмерные комплексы Π должны быть порядка единицы. Итак, время пересечения звездой квазисферического скопления по его диаметру равно
|
|
(7.13) |
Средняя угловая скорость вращения плоской галактики
|
|
(7.14) |
Соотношение типа (7.14) можно несколько обобщить, используя для его определения изменения угловой скорости с увеличением расстояния от центра галактики. Обозначая через M(r) массу галактики, заключенной внутри цилиндра рабиуса r (и с высотой, равной толщине галактики), получим для угловой скорости на этом расстоянии
|
|
(7.15) |
С другой стороны, соотношение (7.14) можно проверить по статистической связи между угловой скоростью и размером галактик (рис. 25), поскольку, как можно предполагать, дисперсия масс галактик, вероятно, не слишком велика.
Вращение звездных систем (а следовательно, и связанное с ним распределение массы) определяется начальной эволюцией системы и, с точки зрения численного эксперимента, должно задаваться как начальное условие задачи. Естественно, что при этом приходится в основном исходить из наблюдательных данных. Как для нашей Галактики, так и для ряда других спиральных галактик были получены детальные распределения угловых скоростей и масс в плоскости диска. Имеются и статистические данные.
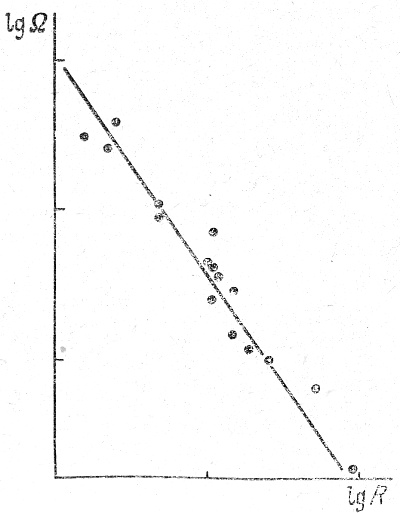
Рис. 25. Зависимость между угловой скоростью вращения галактик и их размером.
Прямая линия соответствует зависимости Ω ∼ R-3/2
Например, на рис. 26 приведены статистические зависимости между массой галактики ![]() и ее моментом вращения
и ее моментом вращения ![]() или кинетической энергией вращения W [1]. Прямая линия соответствует эмпирической формуле
или кинетической энергией вращения W [1]. Прямая линия соответствует эмпирической формуле
|
|
(7.16) |
В работе [2] было найдено, что безразмерный комплекс
|
|
(7.17) |
обладает более слабой зависимостью от геометрии системы и распределения масс внутри системы.
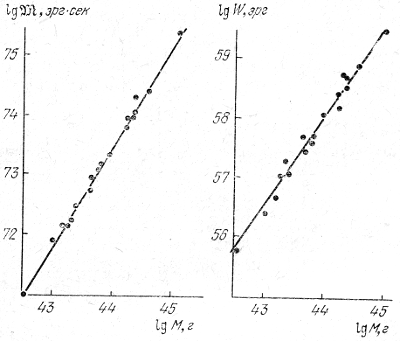
Рис. 26. Зависимость между вращательным моментом ![]() и массой
и массой ![]() (слева) и между энергией вращения W и массой
(слева) и между энергией вращения W и массой ![]() (справа) для спиральных галактик.
(справа) для спиральных галактик.
Исследованию вращения звездных систем было посвящен очень много работ, но поскольку уверенных общих соотношений пока нет, в численных экспериментах обычно выбирают простейшие модели, как например, случай твердотельного вращения.
<< § 6.4 Численное моделирование вспышек и коллапса звезд | Оглавление | § 7.2 Время релаксации звездных систем >>