




Next: 12 самосопряженные (эрмитовы) преобразования
Previous: 10 инвариантные подпространства
Subsections
[section] Рассматривается линейное пространство над полем
комплексных числел.
Мы рассматривали ранее в аффинном пространстве отдельно линейные
преобразования и отдельно билинейные формы. В случае евклидова
пространства между билинейными формами и линейными преобразованиями
существует тесная связь3.5.
Всякому линейному преобразованию  отвечает в евклидовом
пространстве билинейная форма отвечает в евклидовом
пространстве билинейная форма 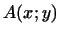 , задаваемая формулой , задаваемая формулой
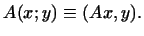 Действительно, функция
Действительно, функция
 удовлетворяет
условиям, определяющим билинейную форму. Имеем: удовлетворяет
условиям, определяющим билинейную форму. Имеем:
1
![\begin{displaymath}\begin{gathered}[t]
(A(x_1+x_2),y)=(Ax_1+Ax_2,y)=(Ax_1,y)+(Ax...
...\\
(A\lambda x,y)=(\lambda Ax,y)=\lambda (Ax,y).\end{gathered}\end{displaymath}](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img340.gif)
2
![\begin{displaymath}\begin{gathered}[t]
(x,A(y_1+y_2))=(x,Ay_1+Ay_2)=(x,Ay_1)+(x,Ay_2),\\
(x,A\mu y)=(x,\mu Ay)=\bar\mu (x,Ay).\end{gathered}\end{displaymath}](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img341.gif)
Покажем, что преобразование  определяется соответствующей
билинейной формой определяется соответствующей
билинейной формой 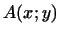 однозначно. однозначно.
Пусть
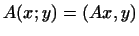 и
и
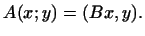 Тогда
Тогда
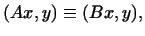 т.е.
т.е.
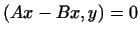 для любого вектора
для любого вектора  ; но это значит, что ; но это значит, что
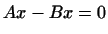 . Таким образом, . Таким образом, 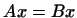 для любого для любого 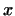 , т.е. , т.е.
 . Однозначность доказана. . Однозначность доказана.
Имеет место и обратное.
Пусть  -- комплексное евклидово пространство и пусть -- комплексное евклидово пространство и пусть 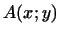 --
билинейная форма в нем. Выберем в --
билинейная форма в нем. Выберем в  какой-либо ортогональный
нормированный базис какой-либо ортогональный
нормированный базис
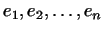 . Если . Если
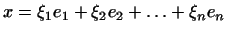 и и то
то 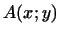 можно записать в виде можно записать в виде
Постараемся представить это выражение в виде некоторого скалярного
произведения. Для этого перепишем его следующим образом:
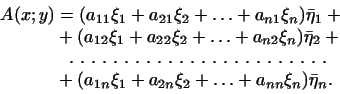 Введем в рассмотрение вектор
Введем в рассмотрение вектор 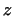 с координатами с координатами
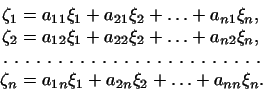 Вектор
Вектор 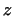 получается из вектора получается из вектора 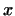 линейным преобразованием с
матрицей, транспонированной к матрице линейным преобразованием с
матрицей, транспонированной к матрице
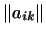 билинейной формы билинейной формы
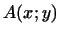 . Это преобразование мы обозначим буквой . Это преобразование мы обозначим буквой  , т.е. положим , т.е. положим
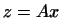 . Мы получаем, следовательно, что . Мы получаем, следовательно, что
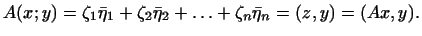 Итак, всякой билинейной форме
Итак, всякой билинейной форме 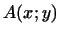 в евклидовом
пространстве отвечает такое линейное преобразование в евклидовом
пространстве отвечает такое линейное преобразование  , что , что
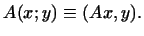
Таким образом, мы доказали следующую теорему.
Теорема 11.1
Формула
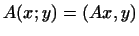 |
(2) |
устанавливает в евклидовом пространстве взаимно однозначное
соответствие между билинейными формами и линейными
преобразованиями.
Из однозначности соответствия, устанавливаемого формулой (2),
следует, что оно не зависит от выбора базиса.
Связь между билинейными формами и линейными преобразованиями можно
установить и другим способом. А именно, каждую билинейную форму можно
представить также в виде
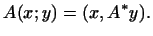
Для этого в формуле (1)
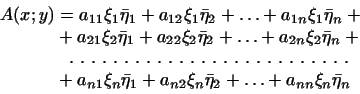 мы будем выносить за скобки координаты
мы будем выносить за скобки координаты
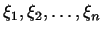 вектора
вектора 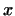 . Повторяя снова прежние рассуждения, мы получаем: . Повторяя снова прежние рассуждения, мы получаем:
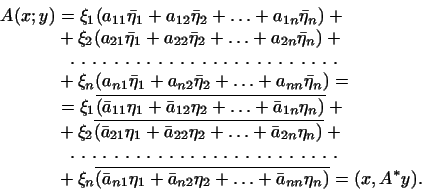
При этом матрица преобразования 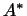 получается из матрицы
преобразования получается из матрицы
преобразования  в любом ортогональном базисе переходом к
транспонированной и заменой ее элементов комплексно сопряженными. в любом ортогональном базисе переходом к
транспонированной и заменой ее элементов комплексно сопряженными.
Заметим, что в неортогональном базисе связь между матрицами
преобразований  и и 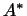 более сложна. более сложна.
Определение 11.1
Пусть  -- линейное преобразование
комплексного евклидова пространства. Преобразование -- линейное преобразование
комплексного евклидова пространства. Преобразование 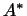 ,
определенное условием ,
определенное условием
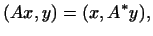 называется
сопряженным к
называется
сопряженным к  . .
Теорема 11.2
В евклидовом пространстве каждому линейному преобразованию отвечает
сопряженное преобразование и притом только одно.
Доказательство. Линейному преобразованию  однозначно соответствует согласно теореме
1 этого параграфа билинейная форма однозначно соответствует согласно теореме
1 этого параграфа билинейная форма
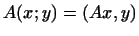 . Эту билинейную
форму согласно сказанному в конце п.1 можно представить, и притом
однозначно, в виде . Эту билинейную
форму согласно сказанному в конце п.1 можно представить, и притом
однозначно, в виде 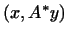 . Окончательно мы имеем: . Окончательно мы имеем:
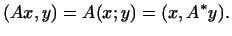

Матрица сопряженного преобразования 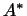 получается из
матрицы преобразования получается из
матрицы преобразования  в ортогональном базисе переходом к
транспонированной и комплексно сопряженной матрице, как это
доказано в п.1 этого параграфа. в ортогональном базисе переходом к
транспонированной и комплексно сопряженной матрице, как это
доказано в п.1 этого параграфа.
Переход от  к к 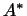 можно выразить в виде правила: если в выражении можно выразить в виде правила: если в выражении
 мы желаем мы желаем  перебросить на второе место, то к нему нужно
приписать перебросить на второе место, то к нему нужно
приписать  . .
Операция перехода от преобразования  к сопряженному преобразованию к сопряженному преобразованию
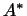 (``операция (``операция  '') связана с определенными выше (§9)
операциями сложения и умножения линейных преобразований следующими
соотношениями: '') связана с определенными выше (§9)
операциями сложения и умножения линейных преобразований следующими
соотношениями:
1
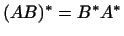 . .
2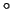
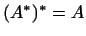 . .
3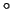
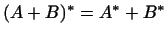 . .
4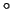
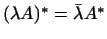 . .
5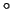 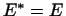 . .
Докажем, например, два первых из этих свойств.
1
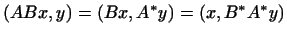 . .
Но, с другой стороны, по определению  имеем: имеем:
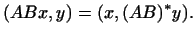 Сравнивая правые части этих двух равенств и вспомнив, что
линейное преобразование однозначно определяется соответствующей
билинейной формой, получаем:
Сравнивая правые части этих двух равенств и вспомнив, что
линейное преобразование однозначно определяется соответствующей
билинейной формой, получаем:
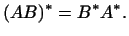
2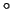 По определению По определению 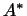 имеем: имеем:
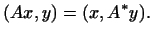 Обозначим временно
Обозначим временно 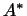 через через 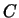 . Тогда . Тогда
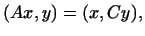 откуда
откуда
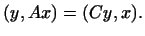 Заменив
Заменив  через через 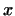 , а , а 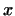 через через  и поменяв местами правую и
левую части этого равенства, получим: и поменяв местами правую и
левую части этого равенства, получим:
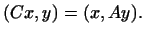 Но это равенство и означает, что
Но это равенство и означает, что 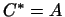 , и так как , и так как 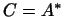 , то , то
Упражнения
1. Доказать таким же способом свойства 3 -5 -5 . .
2. Доказать свойства 1 -5 -5 , пользуясь тем, что матрица
преобразования , пользуясь тем, что матрица
преобразования 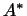 получается из матрицы преобразования получается из матрицы преобразования  в
ортогональном базисе транспонированием и заменой всех элементов
комплексно сопряженными. в
ортогональном базисе транспонированием и заменой всех элементов
комплексно сопряженными.
Операция 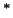 в известной мере аналогична операции перехода от
данного комплексного числа в известной мере аналогична операции перехода от
данного комплексного числа  к сопряженному к сопряженному
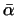 . Эта
аналогия не случайна. Действительно, для матриц первого порядка над
комплексным полем, т.е. для комплексных чисел, операция . Эта
аналогия не случайна. Действительно, для матриц первого порядка над
комплексным полем, т.е. для комплексных чисел, операция 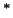 как
раз и состоит в замене данного числа комплексно сопряженным. как
раз и состоит в замене данного числа комплексно сопряженным.
Среди всех комплексных чисел действительные числа характеризуются тем
свойством, что
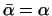 . Для линейных преобразований
аналогичное понятие является весьма существенным. . Для линейных преобразований
аналогичное понятие является весьма существенным.
Определение 11.2
Линейное преобразование  называется
самосопряженным (или эрмитовым),
если называется
самосопряженным (или эрмитовым),
если 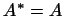 . .
Покажем, что для того, чтобы линейное преобразование  было
самосопряженным, необходимо и достаточно, чтобы билинейная форма было
самосопряженным, необходимо и достаточно, чтобы билинейная форма
 была эрмитовой. была эрмитовой.
В самом деле, эрмитовость формы  означает, что означает, что
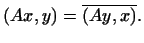 |
(a) |
Самосопряженность преобразования  означает, что означает, что
 |
(b) |
Легко видеть, что равенства (a) и (b) эквивалентны.
Всякое комплексное число 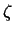 представимо в виде представимо в виде
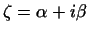 , где , где  и и 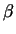 -- действительные
числа. Аналогично: -- действительные
числа. Аналогично:
Всякое линейное преобразование  может быть записано в виде может быть записано в виде
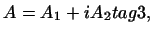 |
(1) |
где 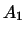 и и 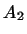 -- самосопряженные преобразования. -- самосопряженные преобразования.
Действительно,
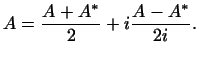 Введем обозначения
Введем обозначения
 Тогда
Тогда
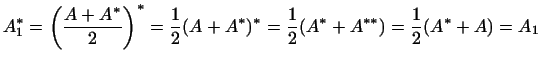 и
и
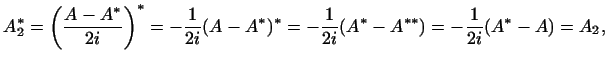 т.е.
т.е. 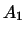 и и 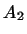 -- самосопряженные преобразования. -- самосопряженные преобразования.
Таким образом, самосопряженные преобразования играют среди всех
линейных преобразований роль, аналогичную роли действительных чисел
среди комплексных.
Упражнения
1. Доказать единственность представления
преобразования  в виде (1). в виде (1).
2. Доказать, что линейная комбинация с действительными
коэффициентами самосопряженных преобразований есть снова
самосопряженное преобразование.
3. Доказать, что если  -- произвольное линейное
преобразование, то преобразования -- произвольное линейное
преобразование, то преобразования 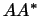 и и 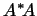 --
самосопряженные. --
самосопряженные.
Примечание. В отличие от комплексных чисел, 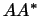 , вообще
говоря, не равно , вообще
говоря, не равно 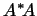 . .
Произведение двух самосопряженных линейных преобразований не есть,
вообще говоря, самосопряженное преобразование. Имеет место следующая
Теорема 11.3
Пусть  и и 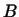 -- самосопряженные линейные преобразования. Для того
чтобы преобразование -- самосопряженные линейные преобразования. Для того
чтобы преобразование 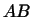 было также самосопряженным, необходимо и
достаточно, чтобы было также самосопряженным, необходимо и
достаточно, чтобы 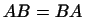 , т.е. чтобы преобразования , т.е. чтобы преобразования  и и 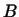 были
перестановочны. были
перестановочны.
Доказательство. Нам дано, что
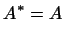 и и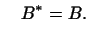 Мы ищем необходимое и достаточное условие того, чтобы выполнялось
равенство
Мы ищем необходимое и достаточное условие того, чтобы выполнялось
равенство
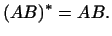 |
(4) |
Но
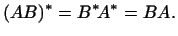 Следовательно, равенство (4) имеет место тогда и только тогда,
когда
Следовательно, равенство (4) имеет место тогда и только тогда,
когда
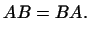 Теорема доказана.
Теорема доказана.
Упражнение
Доказать, что если  и и 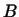 -- самосопряженные
преобразования, то самосопряженными будут и преобразования -- самосопряженные
преобразования, то самосопряженными будут и преобразования  и и
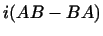 . .
Аналогом комплексных чисел, равных по модулю единице, т.е. таких, что
 , являются унитарные преобразования. , являются унитарные преобразования.
Определение 11.3
Линейное преобразование  называется
унитарным, если называется
унитарным, если
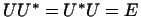 3.6.
Другими словами, для унитарного преобразования 3.6.
Другими словами, для унитарного преобразования
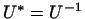 . .
В §13 мы познакомимся с весьма простой геометрической
интерпретацией унитарных преобразований.
Упражнения
1. Доказать, что произведение двух унитарных
преобразований есть снова унитарное преобразование.
2. Показать, что если  -- унитарное преобразование, а -- унитарное преобразование, а  --
самосопряженное преобразование, то --
самосопряженное преобразование, то 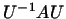 -- также
самосопряженное. -- также
самосопряженное.
Ниже (в §15) мы докажем, что всякое линейное преобразование можно
представить как произведение самосопряженного на унитарное. Эту
теорему можно рассматривать как обобщение записи комплексного числа в
тригонометрической форме.
Введем еще одно определение.
Определение 11.4
Линейное преобразование  называется
нормальным,
если называется
нормальным,
если
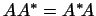 . .
Для комплексных чисел нет надобности в аналогичном понятии, так как
умножение комплексных чисел коммутативно и, значит,
 всегда равно
всегда равно
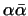 . .
Нетрудно убедиться, что как самосопряженные, так и унитарные
преобразования являются частными случаями нормальных
преобразований.
Более детальному изучению отдельных классов линейных преобразований в
евклидовом пространстве будут посвящены дальнейшие параграфы этой
главы. При этом мы получим для различных типов преобразований весьма
простую геометрическую характеристику.





Next: 12 самосопряженные (эрмитовы) преобразования
Previous: 10 инвариантные подпространства
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
| 
