В.П.Ильин, доктор физико-математических наук, профессор,
главный научный сотрудник
Института вычислительной математики и математической геофизки СО РАН.
Опубликовано в журнале "Природа", N 6, 1999 г.
| Содержание
|
Одна из генеральных линий развития итерационных методов заключается в обобщении
булеевского принципа компенсации (5) на основе перехода к системе так называемых пробных
векторов Yq, для которых должны выполняться равенства
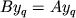 , , 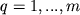 |
(6) |
Здесь результаты получены для уникального класса вещественных блочно-
трехдиагональных матриц - стилтьесовых, которые, с одной стороны, лежат в основе решения
широкого класса практических задач, а с другой - обладают свойствами, полезными при
исследовании основанных на них алгоритмов. Главные из этих свойств - симметричность,
положительность собственных чисел и монотонность (обратная матрица A-1 имеет
неотрицательные элементы).
Изначальный вопрос здесь: для каких наборов пробных векторов 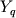 вообще разрешима
задача о вычислении предобусловливающей матрицы B рассматриваемого факторизованного
вида? Изучение проблемы привело автора к новому понятию в линейной алгебре - сильной
независимости векторов. Если в матрице размером вообще разрешима
задача о вычислении предобусловливающей матрицы B рассматриваемого факторизованного
вида? Изучение проблемы привело автора к новому понятию в линейной алгебре - сильной
независимости векторов. Если в матрице размером 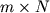 , составленной из m векторов , составленной из m векторов 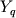 порядка
порядка 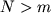 , каждый минор m-го порядка ненулевой, то такие векторы назовем сильно
независимыми. Подчеркнем, что обычной, линейной, независимости векторов (когда хотя бы
один минор ненулевой) недостаточно для разрешимости задачи (6). , каждый минор m-го порядка ненулевой, то такие векторы назовем сильно
независимыми. Подчеркнем, что обычной, линейной, независимости векторов (когда хотя бы
один минор ненулевой) недостаточно для разрешимости задачи (6).
Далее следуют обычные для вычислительной математики вопросы, на которые удалось
получить первые обнадеживающие ответы: как конструктивно построить экономичный
алгоритм по условию (6)? Какова его чувствительность и устойчивость к погрешностям
округлений машинных операций? При каких пробных векторах предобусловливающая матрица
B будет симметричной и положительно определенной (что необходимо, если требуется
исследовать сами методы неполной факторизации)? Сколько и каких пробных векторов надо
брать, чтобы эффективность алгоритма была по возможности высокой (мы сознательно не
употребляем слова "наивысшей")? Какова будет скорость сходимости итераций? Поиск
решений - новое направление, выходящее за рамки теории только итерационных алгоритмов.
Уравнения (6) можно интерпретировать как обратную обобщенную задачу на
собственные значения: для заданных собственных векторов 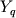 и матрицы A найти матрицу B
(среди рассматриваемого класса ленточных матриц), которая соответствует единичному
обобщенному собственному числу. Такая нетрадиционная задача линейной алгебры, для
которой уже найдены некоторые частные решения, наверняка найдет свою нишу в различных
приложениях. и матрицы A найти матрицу B
(среди рассматриваемого класса ленточных матриц), которая соответствует единичному
обобщенному собственному числу. Такая нетрадиционная задача линейной алгебры, для
которой уже найдены некоторые частные решения, наверняка найдет свою нишу в различных
приложениях.
Другой аспект принципа обобщенной компенсации имеет прямое отношение к теории
приближений. Если начальную ошибку итераций представить в виде линейной комбинации
пробных векторов:
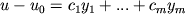 , , |
(7) |
то первое итерационное приближение u1 в (3) при 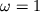 уже будет точным решением.
Справедливо и более сильное утверждение: среди систем сильно независимых пробных
векторов оптимальна та, которая наилучшим образом приближает искомое решение u (при
u0 = 0). А поиск таких приближений уже можно проводить с помощью априорных оценок для
дифференциальных краевых задач. уже будет точным решением.
Справедливо и более сильное утверждение: среди систем сильно независимых пробных
векторов оптимальна та, которая наилучшим образом приближает искомое решение u (при
u0 = 0). А поиск таких приближений уже можно проводить с помощью априорных оценок для
дифференциальных краевых задач.
И наконец, третий важный момент, чисто алгебраический: соотношение (7) позволяет
исследовать итерационные процессы вида (3) в подпространстве, натянутом на векторы 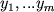 ,
- что тоже является актуальной задачей серьезного теоретического и практического значения. ,
- что тоже является актуальной задачей серьезного теоретического и практического значения.
Одна из общих современных проблем вычислительной математики - построение
адаптивных алгоритмов, подстраивающихся под свойства решаемой задачи и повышающих при
этом свою эффективность на основе анализа априорной и/или апостериорной информации.
Наибольшее значение такое качество имеет при решении трудоемких задач. В математической
физике к таковым относятся "жесткие" уравнения с очень резко меняющимися свойствами
решений. В качестве примера можно привести анизотропное уравнение стационарной
диффузии (или теплопроводности)
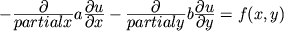 , , |
(8) |
в котором коэффициенты a, b могут сильно изменяться (даже на несколько порядков величины)
и иметь в том числе большие разрывы. У краевых задач подобного рода очень "плохие"
решения, которые порождают главные проблемы с качеством аппроксимации, правда, здесь
они волнуют нас в меньшей степени. Другая особенность такой задачи заключается в
катастрофически плохой обусловленности алгебраической системы, получаемой после
дискретизации. Помимо потери вычислительной устойчивости, это приводит, как правило, к
значительному увеличению количества итераций 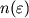 . В работах автора с Б.Келлогом (США) на
примере простейшего итерационного метода Зейделя, по-видимому, впервые было замечено,
что если вычисления каждого следующего приближения проводить последовательно по узлам,
упорядоченным с учетом направления изменений коэффициентов исходных уравнений, то
наличие их больших градиентов можно обратить в свою же пользу. Получается парадоксальный
на первый взгляд феномен: ухудшение алгебраических свойств системы приводит к улучшению
итерационного алгоритма, если он нужным образом адаптирован. . В работах автора с Б.Келлогом (США) на
примере простейшего итерационного метода Зейделя, по-видимому, впервые было замечено,
что если вычисления каждого следующего приближения проводить последовательно по узлам,
упорядоченным с учетом направления изменений коэффициентов исходных уравнений, то
наличие их больших градиентов можно обратить в свою же пользу. Получается парадоксальный
на первый взгляд феномен: ухудшение алгебраических свойств системы приводит к улучшению
итерационного алгоритма, если он нужным образом адаптирован.
Этот результат удалось перенести и на такие "идеологически" сложные алгоритмы, как
методы неполной факторизации. Доказан принципиальный факт ускорения сходимости
адаптивных алгоритмов при монотонном изменении коэффициентов исходной системы.
Выведенные теоретические оценки наглядно подтверждаются численными экспериментами. В
двух словах, полученные утверждения можно объяснить следующим образом. При адаптивном
построении предобусловливающая матрица B "наследует" и компенсирует плохие свойства
исходной матрицы A, в результате чего качество итогового алгоритма только улучшается.
Аналогичный эффект наблюдается и в случае очень сильной анизотропии (например,
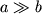 ), даже если коэффициенты постоянны. Хотя при этом обусловленность исходной
системы тоже ухудшается, в определенном смысле задача приближается к одномерной, и при
соответствующем блочном упорядочении неизвестных итерационный алгоритм сводится к
безытерационному. ), даже если коэффициенты постоянны. Хотя при этом обусловленность исходной
системы тоже ухудшается, в определенном смысле задача приближается к одномерной, и при
соответствующем блочном упорядочении неизвестных итерационный алгоритм сводится к
безытерационному.
Важно отметить, что адаптивные качества итерационных алгоритмов определяются
непосредственно свойствами алгебраической системы. А ее элементы зависят как от поведения
коэффициентов дифференциальной задачи, так и от шагов сетки. Поэтому рассматриваемые
вычислительные явления могут быть вызваны не "физическими", а чисто дискретизационными
эффектами: если сетка слишком неравномерная (а при сильной разномасштабности деталей
расчетной области шаги могут отличаться в сотни и тысячи раз), то обусловленность матрицы A
сильно ухудшается, но путем соответствующего упорядочения узлов можно сходимость
итераций, наоборот, улучшить.
Исследование и построение таких адаптивных алгоритмов сильно усложняются, если
коэффициенты уравнений описываются немонотонными функциями с многочисленными
экстремальными точками. Имеющийся опыт по исследованию простейшего метода Зейделя в
таких ситуациях позволяет надеяться, что проблемы здесь чисто технического характера: во-
первых, в автоматизации определения "хитрых" последовательностей с монотонными
свойствами и, во-вторых, в обнаружении необходимых свойств матриц с более сложными
блочными структурами.
Отметим, что рассмотренный адаптивный подход выпадает из большой серии работ
известных авторов. Эти работы посвящены обоснованию различных итерационных алгоритмов,
у которых скорость сходимости не зависит от величины разброса исходных коэффициентов.
Однако противоречия здесь на самом деле нет, так как построение адаптивных алгоритмов -
это использование дополнительной информации о внутренних свойствах задачи.
Назад | Вперед
Написать комментарий
|

