М. И. Анохин, Н. П. Варновский, В. М. Сидельников, В. В. Ященко "КРИПТОГРАФИЯ В БАНКОВСКОМ ДЕЛЕ"

Документ взят из кэша поисковой машины. Адрес оригинального документа : http://geo.web.ru/db/msg.html?mid=1161287&uri=node158.html
Дата изменения: Unknown
Дата индексирования: Wed Apr 13 13:06:36 2016
Кодировка: koi8-r

М. И. Анохин, Н. П. Варновский, В. М. Сидельников, В. В. Ященко "КРИПТОГРАФИЯ В БАНКОВСКОМ ДЕЛЕ" - Все о Геологии (geo.web.ru)

Геовикипедия
wiki.web.ru

Поиск

Главная страница

Конференции: Календарь / Материалы

Каталог ссылок

Словарь

Форумы

В помощь студенту

Последние поступления

Геология | Книги

Обсудить в форуме

Добавить новое сообщение

Вперед: 12.4 Метод решета числового поля Вверх: 12.3 Факторизация чисел с субэкспоненциальной сложностью Назад: 12.3.4 Метод квадратичного решета Содержание Предметный указатель

12.3.5 Другие методы

Для факторизации целых чисел существует также 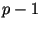-метод Полларда. Недавно он усовершенствован в работе [MonS]. В нем отсутствуют какие-либо оценки сложности, однако из идей этого метода возник метод факторизации с помощью эллиптических кривых, который имеет наилучшую оценку сложности среди субэкспоненциальных алгоритмов. Описание метода см. в [Len87], [Mont], [Kob]. 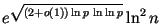Эвристическая оценка сложности составляет $e^{\sqrt{(2+o(1))\ln p\,\ln\ln p}}\ln^2n$ арифметических операций, где -- наименьший простой делитель . 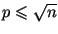Если вспомнить, что $p\leqslant\sqrt n$ , то получим оценку сложности 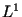. Метод запрограммирован и широко применяется.

Михаил Анохин

Проект осуществляется при поддержке:
Геологического факультета МГУ,
РФФИ