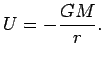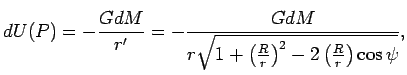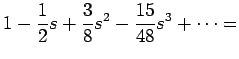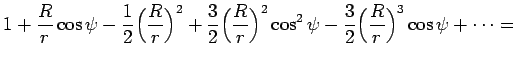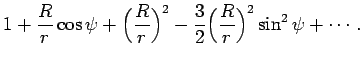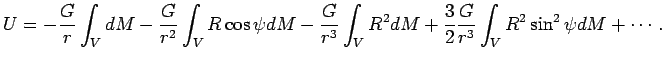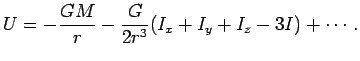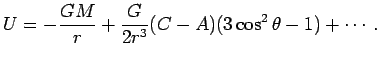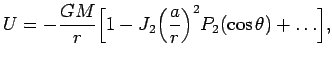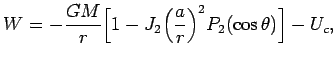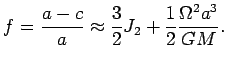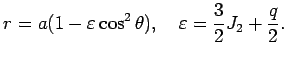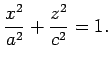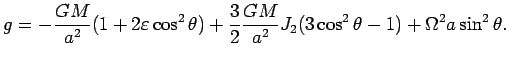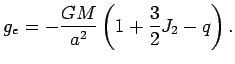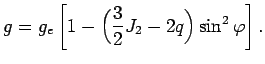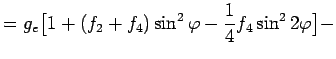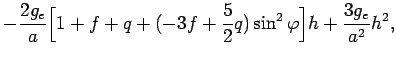Астронет | Картинка дня | Обзоры astro-ph | Новости | Статьи | Книги | Карта неба | Созвездия | Переменные Звезды | Глоссарий

Физика космоса | Биографии | Словарь | Ключевые слова | Астрономия в России | Форумы | Семинары | Сверхновые

<< 4.1. Основные параметры Земли | Оглавление | 4.3. Геоцентрическая и геодезическая >>

4.2. Уравнение геоида

Для вычисления уравнения геоида используем формулу (4.1) и вычислим потенциал притяжения тела произвольной формы. Полученные выражения будут использоваться при вычислении прецессионного и нутационного движения осей Земли.

Потенциал точки с массой на расстоянии равен:

Сила притяжения этой точки другой точки с массой равна:

Подставляя в (4.5) выражение (4.4) и используя (4.3), получим хорошо известную формулу Ньютона:

- единичный вектор, направленный от точки с массой к точке с массой .

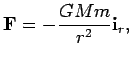
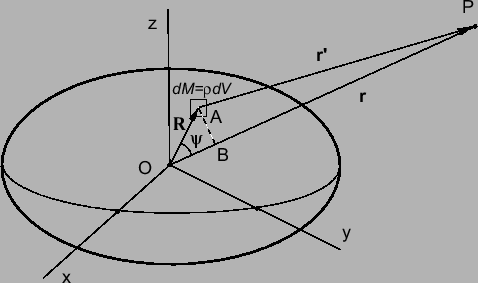
Используем выражение для потенциала точки (4.4) и найдем потенциал притяжения элемента массы тела произвольной формы в точке ( - плотность, зависящая от координат элемента объема ). Для этого определим систему координат с началом в центре масс тела (рис. 4.1).

Будем считать, что точка расположена вне тела. Расстояние от точки до элемента массы , находящегося в точке с координатами , равно , а до точки равно . Тогда потенциал в точке равен

где - расстояние от точки до точки , - угол между отрезками и . Найдем разложение знаменателя по степеням до членов третьего порядка, предполагая, что :

Традиционное представление потенциала имеет вид:

где - полиномы Лежандра (см. приложение A.6). Индекс называется степенью полинома Лежандра, причем

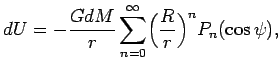
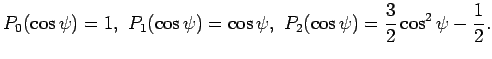
Чтобы найти потенциал в точке от всех точек тела, проинтегрируем (4.6) во всему объему тела, используя разложение (4.7):

Первый член соответствует потенциалу точки с массой , расположенной в начале координат . Второй член равен нулю, так как начало координат совпадает с центром масс тела. Это легко доказать. В самом деле, центр масс тела - это точка , радиус-вектор которой относительно некоторой системы координат равен:

где -радиус-вектор элемента массы . Если центр масс тела совпадает с началом системы координат, то , следовательно . Это доказывает утверждение, что второй член в (4.8) равен нулю.

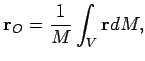
Определим осевые моменты инерции Земли относительно осей , соответственно, следующим образом:

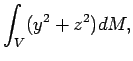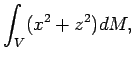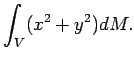Тогда третий член в (4.8) можно представить в виде:

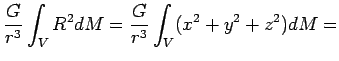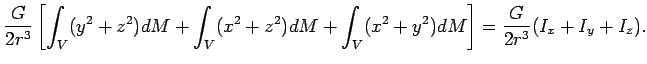Так как произведение равно перпендикуляру , опущенному из точки на прямую , то четвертый интеграл в (4.8) равен моменту инерции тела относительно оси . Следовательно, гравитационный потенциал потенциал тела произвольной формы в точке , расположенной вне тела, равен:

Выразим теперь момент инерции тела относительно оси через направляющие косинусы этой прямой относительно осей . Пусть . Тогда

Так как вектор имеет компоненты , то имеем согласно (2.17):

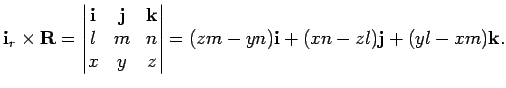
Отсюда

Раскрывая скобки и подставляя в четвертый интеграл в (4.8), получим:

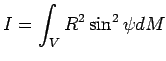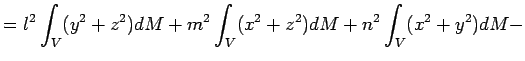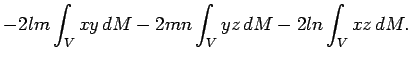Интегралы

называются центробежными моментами инерции твердого тела. Осевые и центробежные моменты инерции тела определяют его тензор инерции:

В системе главных осей недиагональные компоненты тензора равны нулю, а осевые (или главные) моменты относительно осей обозначим как , соответственно, т.е. тензор инерции имеет вид

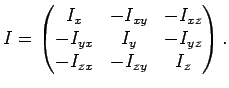
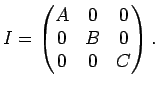
Таким образом, если координатные оси системы совпадают с главными осями тензора инерции, то

Обозначим угол между и осью через . Тогда

Предположим, что . В этом случае момент инерции равен

Подставляя в (4.9) найдем окончательное выражение для гравитационного потенциала в точке :

Для Земли главные моменты инерции равны    кг$·$ м$^2$,    кг$·$ м$^2$,    кг$·$ м$^2$,    кг$·$ м$^2$. Относительная разность экваториальных моментов и равна . Поэтому часто считают, что и тем самым полагают, что Земля - двухосный эллипсоид или эллипсоид вращения. Гравитационный потенциал Земли называется геопотенциалом.

Перепишем (4.10) в следующем виде:

где называется динамическим форм-фактором Земли, - экваториальный радиус Земли ( м). Приведенные значения взяты из стандартов Международной службы вращения Земли (IERS2003).

Уравнение (4.11) в пределе должно выполняться на поверхности Земли. Если ограничиться разложением до , то полный геопотенциал на поверхности Земли равен:

где - центробежный потенциал. Запишем его в виде:

Так как геоид определяется как поверхность постоянного потенциала, приравняем потенциал на полюсе и экваторе Земли, учитывая, что при ( - полярный радиус Земли), а при :

Отсюда

Определяя геометрическое сжатие эллипсоида как и замечая, что второй член в скобках имеет величину порядка , получим

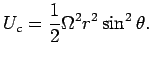
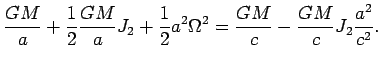
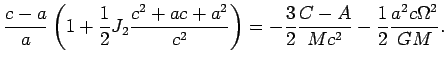
Формула верна с точностью до .

Чтобы найти уравнение поверхности геоида, перепишем формулу (4.12) в следующем виде:

где

- отношение центростремительного ускорения к ускорению силы тяжести на экваторе (при отсутствии вращения). Так как на поверхности геоида величина потенциала постоянна, приравняем его потенциалу на экваторе ( ):

Тогда

Так как величины , то ошибка отбрасывания членов порядка и т.д. сравнима по величине с отброшенными членами в разложении потенциала силы тяжести. Сохраняя лишь линейные члены при разложении знаменателя, получим

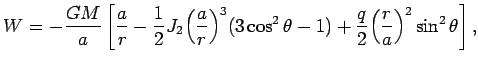
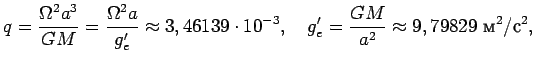
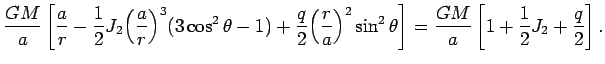
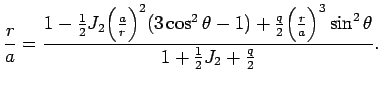
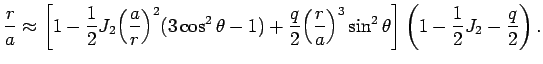
Так как с ошибкой , то перемножая скобки и пренебрегая членами, содержащими произведения малых величин, запишем уравнение геоида в виде

В первом приближении уравнение геоида представляет фигуру, близкую к эллипсоиду с геометрическим сжатием .

В самом деле, рассмотрим меридиональное сечение двухосного эллипсоида, которое является эллипсом с большой и малой полуосями:

Так как малая полуось равна и , , то из (4.15) получим:

Это - точное уравнение эллипса. Если сжатие мало, то, разлагая квадратный корень в ряд по и сохраняя только члены первого порядка, находим:

С точностью до первого порядка сжатие равно: .

В настоящее время коэффициент определяется по наблюдениям искусственных спутников Земли. Забегая вперед, скажем, что по скорости прецессии определяется динамическое сжатие Земли

Используя определения параметров и , найдем полярный момент инерции Земли:

Так как моменты инерции определяются плотностью вещества внутри тела, то вычисленное на основе наблюдений значение полярного момента инерции Земли представляет одно из основных условий, которым должно удовлетворять радиальное распределение плотности внутри Земли. Момент инерции Земли меньше момента инерции однородного шара, для которого численный множитель равен 0,4, и, следовательно, плотность вещества внутри Земли должна увеличиваться к центру Земли.

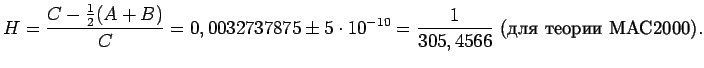
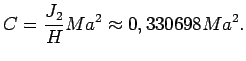
Найдем теперь ускорение силы тяжести на геоиде. Для этого достаточно продифференцировать полный геопотенциал (4.12). Так как , то с учетом (4.3) найдем, что модуль равен:

Второй член имеет величину порядка  (4.14). Поэтому с точностью до , получим:

На поверхности геоида выполняется равенство: . Поэтому

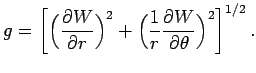
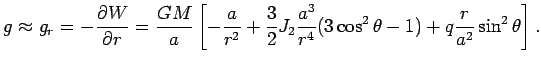
Отсюда ускорение силы тяжести на экваторе равно:

Знак минус в формуле (4.17) подчеркивает тот факт, что радиальная компонента направлена в противоположную сторону, чем единичный вектор . В соответствии с принятыми значениями постоянных равно (см. табл. 9.2): . Используя определение  (4.17) и (4.16), найдем ускорение силы тяжести на широте :

Более точное выражение для ускорения силы тяжести , измеряемого в точке с геодезической широтой на высоте над эллипсоидом с полуосями и сжатием , имеет вид:

где

С точностью до членов второго порядка малости величины и равны:

Используя принятые значения постоянных, получим:

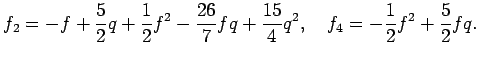
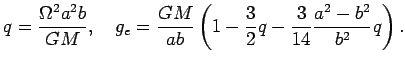
где высота измеряется в метрах.

---

<< 4.1. Основные параметры Земли | Оглавление | 4.3. Геоцентрическая и геодезическая >>

Публикации с ключевыми словами: астрометрия - сферическая астрономия - системы координат - шкалы времени Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
См. также: 80 лет со дня рождения Альберта Петровича Гуляева Руководство по практической работе с каталогом Hipparcos К 70-летию Вилена Валентиновича Нестерова Полная версия "Сферической астрономии" В.Е.Жарова Обзор геостационарной орбиты на двойном астрографе УАФО Отдел пульсарной астрометрии ПРАО АКЦ ФИАН Прямое определение расстояния до центра Галактики Все публикации на ту же тему >>