Next: 2 Тангенс
Up: Первое знакомство с тригонометрией
Previous: Первое знакомство с тригонометрией
Subsections
|
Классификация углов из книги по
альпинизму:
``Перпендикулярно'' - 60 градусов;
``Мой дорогой сэр, абсолютно
перпендикулярно!'' -
65 градусов;
``Нависающе'' - 70 градусов.
Дж.Литтлвуд. ``Математическая смесь''.
|
Пусть человек поднимается в гору. Будем
считать, что склон горы - это гипотенуза 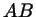 прямоугольного
треугольника прямоугольного
треугольника  (рис. 1, 2). (рис. 1, 2).
Рис. 1:
 |
Рис. 2:
 |
Можно предложить по крайней мере два способа измерения крутизны
подъема: 1) измерить высоту подъема (отрезок 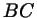 на
рис. 1);
2) провести дугу с центром в точке на
рис. 1);
2) провести дугу с центром в точке  (рис. 2) и измерить ее длину.
(рис. 2) и измерить ее длину.
Конечно, сама по себе высота подъема ничего не характеризует:
если вы долго идете по склону, то можно подняться высоко даже
при пологом склоне. Поэтому нужно рассматривать отношение
длины подъема к длине пути (соответственно отношение длины
дуги к радиусу) 1. Эти отношения от длины пути уже не зависят.
Вот формальное доказательство того, что отношение длины
подъема к длине пути не зависит от этой длины. Пусть человек
прошел не весь путь, а дошел только до точки  (рис. 3). Тогда крутизна подъема на отрезке
(рис. 3). Тогда крутизна подъема на отрезке  равна
равна  , а на отрезке , а на отрезке 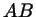 равна равна  . .
Рис. 3:
 |
Однако
 как два перпендикуляра
к одной прямой, так что как два перпендикуляра
к одной прямой, так что
 , ,
 . Стало быть, треугольники . Стало быть, треугольники  и
и  подобны по двум углам, и подобны по двум углам, и
 . Таким
образом, отношение высоты подъема к длине пути не зависит от
длины пути. Доказать, что отношение длины дуги к радиусу не
зависит от радиуса, также можно, но для этого надо формально
определить, что такое длина дуги. В этой книжке мы этим
заниматься не будем. . Таким
образом, отношение высоты подъема к длине пути не зависит от
длины пути. Доказать, что отношение длины дуги к радиусу не
зависит от радиуса, также можно, но для этого надо формально
определить, что такое длина дуги. В этой книжке мы этим
заниматься не будем.
Определение. Синусом острого угла в прямоугольном треугольнике называется
отношение катета этого треугольника, лежащего против угла,
к гипотенузе треугольника (рис. 4).
От выбора прямоугольного треугольника, содержащего угол, это
отношение не зависит.
Рис. 4:
Определение синуса:
 . .
 |
Вторая из введенных нами характеристик крутизны называется
радианной мерой угла.
Определение. Радианной мерой угла
называется отношение длины
дуги окружности, заключенной между сторонами угла и с центром
в вершине угла, к радиусу этой окружности
(рис. 5).
От радиуса окружности это отношение не зависит.
Рис. 5:
Радианная мера угла  - отношение длины дуги - отношение длины дуги 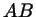 к радиусу к радиусу
 . .
 |
Например, когда говорят, что ``радианная мера угла равна  '',
или ``величина угла равна '',
или ``величина угла равна  радиана'', или попросту ``угол
равен радиана'', или попросту ``угол
равен  радиана'', это значит, что заключенная внутри него
дуга вдвое короче радиуса. Если радиус окружности равен радиана'', это значит, что заключенная внутри него
дуга вдвое короче радиуса. Если радиус окружности равен  , то
радианная мера угла равна длине дуги. , то
радианная мера угла равна длине дуги.
Вычислим радианную меру прямого угла. В соответствии с нашим
определением проведем дугу окружности радиуса  с центром
в вершине прямого угла (рис. 6). Дуга с центром
в вершине прямого угла (рис. 6). Дуга 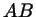 составляет четверть всей окружности. Коль скоро длина окружности
радиуса
составляет четверть всей окружности. Коль скоро длина окружности
радиуса  равна равна  , длина нашей дуги равна , длина нашей дуги равна
 , а радианная мера прямого угла равна , а радианная мера прямого угла равна
 . .
Рис. 6:
 |
Обе введенные нами характеристики крутизны (синус и радианная
мера угла) имеют то преимущество перед привычным измерением углов
в градусах, что являются естественными; про измерение углов
в градусах этого не скажешь: как бы вы стали объяснять
представителю внеземной цивилизации, почему один градус
составляет именно одну девяностую прямого угла? Кстати, во время
Великой французской революции,
когда пытались изменить все, включая календарь и названия
игральных карт, была предложена и новая единица измерения
углов - одна сотая прямого угла, что ничуть не хуже и не лучше одной
девяностой.
Выясним, как связаны между собой радианная и градусная меры
угла. Как мы уже знаем, величина прямого угла равна
 радиан. Так как угол
радиан. Так как угол  в 90 раз меньше прямого угла, то
и его радианная мера в 90 раз меньше радианной меры прямого угла,
то есть равна в 90 раз меньше прямого угла, то
и его радианная мера в 90 раз меньше радианной меры прямого угла,
то есть равна
 . Угол в . Угол в  градусов имеет меру
градусов имеет меру
 радиан. Чтобы узнать, сколько
градусов содержит угол в 1 радиан, надо найти такое радиан. Чтобы узнать, сколько
градусов содержит угол в 1 радиан, надо найти такое  , что , что
 . Стало быть,
в одном радиане содержится . Стало быть,
в одном радиане содержится
 . .
Задача 1.1
Заполните пустые места в таблице, после
чего выучите таблицу наизусть:
Задача 1.2
Для каждого из углов 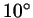 , , 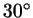 , ,  найдите
приближенные значения синуса и радианной меры (с двумя значащими
цифрами). На сколько процентов отличаются синус и радианная мера
для этих углов? найдите
приближенные значения синуса и радианной меры (с двумя значащими
цифрами). На сколько процентов отличаются синус и радианная мера
для этих углов?
Задача 1.3
Пусть радианная мера острого угла равна 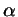 . Докажите
неравенство: . Докажите
неравенство:
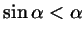 (словами: синус острого угла
меньше его радианной меры). (словами: синус острого угла
меньше его радианной меры).
Указание. См. рис. 7.
Рис. 7:
 |
Написать комментарий
|

