Next: 7 Графики синуса и косинуса
Up: Начальные свойства тригонометрических функций
Previous: 5 Формулы приведения
Будем учиться решать тригонометрические уравнения. Начнем
с самого простого: уравнения  . Мы помним, что . Мы помним, что  - ордината точки
- ордината точки  на тригонометрической окружности. На ней
есть только одна точка с ординатой на тригонометрической окружности. На ней
есть только одна точка с ординатой 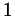 - точка - точка 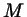 на
рис. 36а. на
рис. 36а.
Рис. 36:
Простейшие уравнения.
 |
Одно из чисел, соответствующих точке 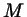 , - это число , - это число  .
Кроме .
Кроме  этой точке соответствуют, очевидно, все числа вида этой точке соответствуют, очевидно, все числа вида
 , где , где 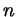 - целое число, и только они. Вместо
`` - целое число, и только они. Вместо
``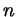 - целое число'' принято писать `` - целое число'' принято писать ``
 ''
(буквальный перевод: `` ''
(буквальный перевод: ``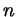 принадлежит множеству всех целых
чисел, обозначаемому принадлежит множеству всех целых
чисел, обозначаемому
 ''). Итак, решения уравнения ''). Итак, решения уравнения  можно записать так:
можно записать так:
 . Можно записать
решения этого уравнения и в виде множества: . Можно записать
решения этого уравнения и в виде множества:
 Можно, наконец, написать так:
Ответ:
Можно, наконец, написать так:
Ответ: 
Решим еще уравнение  . Так как . Так как  - абсцисса
точки, соответствующей - абсцисса
точки, соответствующей  , на тригонометрическом круге числу , на тригонометрическом круге числу  могут соответствовать точки
могут соответствовать точки 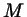 и и  (рис. 36б),
и только они. Точке (рис. 36б),
и только они. Точке 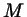 , как мы только что выяснили,
соответствуют числа вида , как мы только что выяснили,
соответствуют числа вида
 . Точке . Точке  соответствует, в частности, число
соответствует, в частности, число 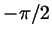 , а значит, и все числа
вида , а значит, и все числа
вида
 ( (
 ). ).
Рис. 37:
Простейшие уравнения:
систематизация
 |  |
Можно записать оба эти множества чисел одной формулой, а именно
 ( (
 ). Убедитесь, что эта формула дает
в точности все числа, которым соответствует точка ). Убедитесь, что эта формула дает
в точности все числа, которым соответствует точка 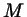 или или  на
рис 36б. на
рис 36б.
Решения этих и аналогичных тригонометрических уравнений
изображены на рис. 37.
Рис. 38:
 |
Прежде чем читать дальше, убедитесь, что решения уравнений на
рис 37 соответствуют рисункам.
Теперь займемся уравнениями посложнее. Решим уравнение
 . Сначала мы опять-таки найдем не сами решения,
а соответствующие им точки на тригонометрическом круге. Это -
точки с ординатой . Сначала мы опять-таки найдем не сами решения,
а соответствующие им точки на тригонометрическом круге. Это -
точки с ординатой  , их, очевидно, две (точки , их, очевидно, две (точки  и и  на рис. 38).
на рис. 38).
Выясним, какие числа соответствуют этим точкам. Точка  соответствует (в частности) числу
соответствует (в частности) числу  ( ( радиан - это радиан - это
 , ,
 ), а точка ), а точка  - числу - числу
 (чтобы пройти путь от начала отсчета (чтобы пройти путь от начала отсчета  до
точки до
точки  , можно сначала пройти в положительном направлении
расстояние , можно сначала пройти в положительном направлении
расстояние  до точки до точки  , а затем вернуться из , а затем вернуться из  в в  ,
пройдя расстояние ,
пройдя расстояние  - дуги - дуги  и и  равны).
Числа, соответствующие точке равны).
Числа, соответствующие точке  , имеют вид , имеют вид
 ,
а числа, соответствующие точке ,
а числа, соответствующие точке  , имеют вид , имеют вид

 . Итак, ответ к уравнению . Итак, ответ к уравнению
 готов: готов:
С уравнением
 нам повезло в том отношении, что мы
смогли явно указать число, синус которого равен нам повезло в том отношении, что мы
смогли явно указать число, синус которого равен  . Чтобы
решить уравнение . Чтобы
решить уравнение  для произвольного для произвольного  , нам нужно
как-то обозначить число, синус которого равен , нам нужно
как-то обозначить число, синус которого равен  . При этом, если
такие числа есть, то их много, так что нужно еще выбрать из них
одно. Эти проблемы принято решать следующим образом: . При этом, если
такие числа есть, то их много, так что нужно еще выбрать из них
одно. Эти проблемы принято решать следующим образом:
Рис. 39:
Арксинус.
 |
Рис. 40:
Уравнение  . .
 |
Определение. Арксинусом числа  называется такое число
называется такое число  , что , что
 и и
 .
Это число обозначается .
Это число обозначается  . .
Из рис. 39 видно, что  существует
и однозначно определен, если существует
и однозначно определен, если
 . Если . Если  (то
есть (то
есть  или или  ), то ), то  не определен, поскольку не определен, поскольку
 не бывает больше 1 или меньше не бывает больше 1 или меньше  . Теперь мы можем
записать в общем виде решения уравнения . Теперь мы можем
записать в общем виде решения уравнения  . Будем для
начала считать, что . Будем для
начала считать, что  . Тогда на тригонометрической
окружности есть две точки с ординатой . Тогда на тригонометрической
окружности есть две точки с ординатой  (рис. 40). (рис. 40).
Точка  соответствует, очевидно, числу соответствует, очевидно, числу  (а также
числам, отличающимся от него на кратные (а также
числам, отличающимся от него на кратные  ). Точка ). Точка  соответствует числу
соответствует числу
 (вспомните уравнение (вспомните уравнение
 , а также формулу приведения , а также формулу приведения
 ). Все
числа, соответствующие этим двум точкам, - это числа ). Все
числа, соответствующие этим двум точкам, - это числа
 и и
 ( (
 . Стало быть, при . Стало быть, при
 ответ к уравнению ответ к уравнению  таков:
таков:
Когда  приближается к 1, две точки с ординатой приближается к 1, две точки с ординатой  на
тригонометрической окружности приближаются друг к дружке, а когда на
тригонометрической окружности приближаются друг к дружке, а когда
 становится равным 1, они сливаются. Сливаются в одну и две
``серии'' решений уравнения становится равным 1, они сливаются. Сливаются в одну и две
``серии'' решений уравнения  : каждая из двух формул
переходит в знакомую нам : каждая из двух формул
переходит в знакомую нам
 . Если же . Если же  (или (или
 ), то уравнение ), то уравнение  не имеет решений: точек
с соответствующей ординатой на тригонометрической окружности
просто нет. не имеет решений: точек
с соответствующей ординатой на тригонометрической окружности
просто нет.
Это напоминает положение дел с уравнением  : если : если  , то
корня два; когда , то
корня два; когда  приближается к нулю, эти корни приближаются
друг к другу, когда приближается к нулю, эти корни приближаются
друг к другу, когда  , два корня сливаются в один, а когда , два корня сливаются в один, а когда
 отрицательно, то корней у уравнения отрицательно, то корней у уравнения  нет. Если,
однако, рассматривать наряду с обычными еще и так называемые
``комплексные числа'', то окажется, что при нет. Если,
однако, рассматривать наряду с обычными еще и так называемые
``комплексные числа'', то окажется, что при  у уравнения у уравнения
 тоже есть два корня, но только комплексных. Аналогичным
образом у уравнения тоже есть два корня, но только комплексных. Аналогичным
образом у уравнения  при при  есть решения,
являющиеся комплексными числами. Об этом у нас пойдет речь в главе 6. есть решения,
являющиеся комплексными числами. Об этом у нас пойдет речь в главе 6.
Решения уравнения  можно записать и одной формулой: можно записать и одной формулой:
 |
(2) |
Проверьте, что формула (2) дает другую запись того
же ответа, что и формула (1) (для этого полезно
отдельно разобрать случай четных 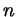 , когда , когда  , и нечетных , и нечетных 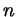 , когда , когда  ). ).
Запись ответа к уравнению  в виде (2)
удобна, если ничего, кроме ответа, от нас не требуется. Если же
нужен дальнейший анализ решений (как, например, в задаче
0.54 в конце параграфа), то запись (1)
(в виде двух ``серий'') удобнее. в виде (2)
удобна, если ничего, кроме ответа, от нас не требуется. Если же
нужен дальнейший анализ решений (как, например, в задаче
0.54 в конце параграфа), то запись (1)
(в виде двух ``серий'') удобнее.
Разберемся теперь с уравнением  . Для записи его
решений используется функция арккосинус. . Для записи его
решений используется функция арккосинус.
Определение.
Арккосинусом числа  называется такое число
называется такое число  , что , что  и и
 .
Это число обозначается .
Это число обозначается  . .
Рис. 41:
Арккосинус.
 |
Из рисунка 41 видно, что  существует
и однозначно определен, если существует
и однозначно определен, если
 , и не определен, если , и не определен, если
 . .
Теперь запишем решения уравнения  . Опять будем сначала
считать, что . Опять будем сначала
считать, что  . Решениям этого уравнения соответствуют
точки с абсциссой . Решениям этого уравнения соответствуют
точки с абсциссой  на тригонометрической окружности
(рис. 42). Точка на тригонометрической окружности
(рис. 42). Точка  соответствует числу соответствует числу  , а точка , а точка  - числу - числу
 (вспомните формулу (вспомните формулу
 ). Вспоминая, что числа, отличающиеся на
кратные ). Вспоминая, что числа, отличающиеся на
кратные  , соответствуют одной и той же точке, получаем, что
при , соответствуют одной и той же точке, получаем, что
при  ответ к уравнению ответ к уравнению  таков:
таков:
Рис. 42:
Уравнение  . .
 |
Если  или или  , этот ответ тоже верен, причем обе
``серии'' сливаются в одну (т.е. одни и те же значения , этот ответ тоже верен, причем обе
``серии'' сливаются в одну (т.е. одни и те же значения  встречаются в обеих сериях); впрочем, при этих значениях
встречаются в обеих сериях); впрочем, при этих значениях  пользоваться общими формулами неразумно. Если же
пользоваться общими формулами неразумно. Если же  , то
уравнение , то
уравнение  не имеет решений. не имеет решений.
Часто решения уравнения  кратко записывают так: кратко записывают так:
 Эта запись имеет те же преимущества и недостатки, что и запись
решений уравнения
Эта запись имеет те же преимущества и недостатки, что и запись
решений уравнения  с помощью одной формулы. с помощью одной формулы.
Для записи решений уравнения
 используется функция
арктангенс. используется функция
арктангенс.
Определение.
Арктангенсом числа  называется такое число
называется такое число  , что , что
 и и
 .
Это число обозначается .
Это число обозначается
 . .
Из рис. 43 видно, что
 существует и однозначно
определен для всех существует и однозначно
определен для всех  . .
Теперь решим уравнение
 . Очевидно, что оно имеет решения
для всех . Очевидно, что оно имеет решения
для всех  и что его решения - числа, соответствующие и что его решения - числа, соответствующие
Рис. 43:
Арктангенс.
 |
точкам  и и  на рис. 43. Точке на рис. 43. Точке  , очевидно,
соответствуют числа , очевидно,
соответствуют числа
 , а точке , а точке  - числа - числа
 (если нанести на тригонометрическую
окружность числа, отличающиеся на (если нанести на тригонометрическую
окружность числа, отличающиеся на  , то получатся две
диаметрально противоположные точки). Получилось две серии
решений. Проще, однако, ответ записать
так: , то получатся две
диаметрально противоположные точки). Получилось две серии
решений. Проще, однако, ответ записать
так:
 Эта запись дает верный ответ, так как при четных
Эта запись дает верный ответ, так как при четных 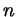 получается
точка получается
точка  , а при нечетных - точка , а при нечетных - точка  . Впрочем, это также следует из
того, что период тангенса равен . Впрочем, это также следует из
того, что период тангенса равен  . .
Осталось еще сказать про уравнение
 . Для его решения
используется малоупотребительная функция арккотангенс. . Для его решения
используется малоупотребительная функция арккотангенс.
Определение. Арккотангенсом
числа  называется такое число называется такое число  , что , что
 и и  .
Обозначается это число .
Обозначается это число
 . .
Арккотангенс, как и арктангенс, определен для всех чисел и связан
с арктангенсом простой формулой (см. задачу 0.49).
Решениями уравнения
 являются числа являются числа
 , ,
 . .
Задача 6.1
Заполните таблицы:
Задача 6.2
Решите уравнения:

Задача 6.3
Решите уравнения:
![$\displaystyle \begin{tabular}{ll}
а) $\sin x=\dfrac{1-\sqrt{5} }{2}$;
&б) $\sin...
...mallskipamount]
л) $\mathop{\mathrm{ctg}}\nolimits x=4-\sqrt{7}$.
\end{tabular}$](http://images.nature.web.ru/nature/2000/12/28/0001158396//s2img342.preview.gif)
Задача 6.4
Решите уравнения:

Задача 6.5
Докажите формулы:

Задача 6.6
Постройте графики функций:

Задача 6.7
Упростите выражения:
![$\displaystyle \begin{tabular}{ll}
а) $\mathop{\mathrm{arctg}}\nolimits \Bigl(\m...
...mits 8)$;
& г) $\arccos(\cos 11)$;\\ [1pt]
д) $\arccos(\sin11)$.
\end{tabular}$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img346.gif)
Задача 6.8
Для каких  верны равенства: верны равенства:

Задача 6.9
Упростите выражения:
![$\displaystyle \begin{tabular}{ll}
а) $\sin\Bigl(\mathop{\mathrm{arctg}}\nolimit...
...amount]
д) $\cos\biggl(\arcsin\Bigl(-\dfrac{1}{3}\Bigr)\biggr)$.
\end{tabular}$](http://images.nature.web.ru/nature/2000/12/28/0001158396//s2img348.preview.gif)
Задача 6.10
а) Сколько решений уравнения
 лежит
на отрезке лежит
на отрезке ![$ [0;10\pi]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img349.gif) ? ?
б) Сколько решений уравнения
 лежит
на отрезке лежит
на отрезке
![$ [0;100\pi]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img351.gif) ? ?
в) Найдите сумму решений уравнения
 , лежащих на отрезке , лежащих на отрезке ![$ [0;64\pi]$](http://images.nature.web.ru/nature/2000/12/28/0001158396/s2img353.gif) . .
Написать комментарий
|

