<< 2.3 Частные случаи политропных ...
| Оглавление |
2.5 Горячие звезды >>
Из наблюдений известно, что массы белых карликов порядка солнечной, но размеры
составляют лишь сотую часть солнечного радиуса (и даже меньше), т.е. белые карлики
представляют собой звезды с чрезвычайно большой плотностью вещества
 г г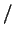 см см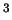 . В таком состоянии обычные атомы разрушаются,
а вещество состоит из ядер и свободных электронов, которые подчиняются статистике
Ферми-Дирака. . В таком состоянии обычные атомы разрушаются,
а вещество состоит из ядер и свободных электронов, которые подчиняются статистике
Ферми-Дирака.
Получим уравнение состояния для вещества белых карликов.
В импульсном пространстве число клеток (состояний) в 1 см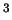 равно
равно
 , где , где
 -- объем
одной клетки (фазовой ячейки). Согласно статистике Ферми-Дирака, в
одном состоянии может находиться только один электрон, и полное
число электронов -- объем
одной клетки (фазовой ячейки). Согласно статистике Ферми-Дирака, в
одном состоянии может находиться только один электрон, и полное
число электронов 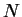 , заключенное в фазовом объеме , заключенное в фазовом объеме
 , с учетом спина равно , с учетом спина равно
 Здесь
Здесь
 -- граничный
импульс Ферми, выше которого при -- граничный
импульс Ферми, выше которого при 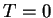 все уровни свободны. Итак,
число электронов в одном кубическом сантиметре все уровни свободны. Итак,
число электронов в одном кубическом сантиметре
 Удобно выражать
Удобно выражать
 в единицах в единицах  ,
вводя безразмерный параметр ,
вводя безразмерный параметр
 .
Тогда .
Тогда
 .
Параметр .
Параметр 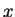 является мерой релятивизма: при является мерой релятивизма: при  электроны
нерелятивистские, при электроны
нерелятивистские, при  ультрарелятивистские. Какой
плотности вещества соответствует данный ультрарелятивистские. Какой
плотности вещества соответствует данный 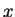 ? Обозначим через ? Обозначим через
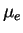 молекулярный вес на один электрон, т.е. среднее число
нуклонов на один электрон ( молекулярный вес на один электрон, т.е. среднее число
нуклонов на один электрон ( для водорода, для водорода,  для для
 и и  для для
 ). Тогда ). Тогда
 г г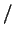 см см![$ ^3]$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img184.gif) . Отсюда следует, что при . Отсюда следует, что при
 г г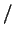 см см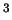 имеем имеем  , т.е. , т.е.
 , и электроны нерелятивистские. При , и электроны нерелятивистские. При
 г г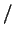 см см . .
Для водорода  осуществляется при плотности осуществляется при плотности
 г г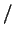 см см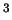 (для (для
 это
соответствует это
соответствует
 г г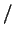 см см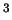 ). Ферми-энергия
электронов в этих условиях ). Ферми-энергия
электронов в этих условиях
 , что в десятки
раз превышает энергию связи электронов атома водорода
( , что в десятки
раз превышает энергию связи электронов атома водорода
(
 ). Таким образом, при ). Таким образом, при  уже
можно пользоваться теорией вырожденного электронного газа. уже
можно пользоваться теорией вырожденного электронного газа.
Рассмотрим нерелятивистскую область  . Средняя энергия
электронов в шаре с объемом . Средняя энергия
электронов в шаре с объемом
 равна
равна
 , т.е. , т.е.
 .
Давление .
Давление
 , т.е. холодное нерелятивистское вещество
представляет собой газ, подчиняющийся уравнению состояния с , т.е. холодное нерелятивистское вещество
представляет собой газ, подчиняющийся уравнению состояния с
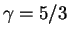 : :
 Статистика Ферми (принцип Паули) определяет константу.
Для идеального (неквантового) газа
Статистика Ферми (принцип Паули) определяет константу.
Для идеального (неквантового) газа
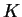 может быть любым. Если охлаждать горячий газ до температуры может быть любым. Если охлаждать горячий газ до температуры
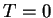 , то , то 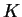 идет не в нуль, а стремится к определенному пределу.
Ферми-движение электронов играет роль температуры. идет не в нуль, а стремится к определенному пределу.
Ферми-движение электронов играет роль температуры.
З а д а ч а. Получите точную формулу для давления вырожденного нерелятивистского
газа
 эрг эрг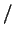 см см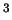 и найдите выражение для и найдите выражение для 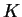 через
фундаментальные константы. через
фундаментальные константы.
Вспоминая общие формулы, выведенные для политропных конфигураций, имеем ( ): ):

Приведем характеристики типичного белого карлика, состоящего из гелия ( )
с массой )
с массой
 г г г г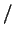 см см г г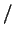 см см см. см.
Строго говоря, полученные выше результаты относятся к абсолютно
холодному веществу. Вещество белых карликов, которые мы наблюдаем,
имеют отличную от нуля температуру (они светят!). Но температура
даже в несколько миллионов градусов мала по сравнению с
характерной ферми-энергией электронов (
 ).
Поэтому тепловое движение плазмы не существенно при расчете
равновесия и устойчивости белых карликов, хотя для расчета их
охлаждения оно важно. ).
Поэтому тепловое движение плазмы не существенно при расчете
равновесия и устойчивости белых карликов, хотя для расчета их
охлаждения оно важно.
С увеличением массы белого карлика растет 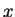 , и при некоторой величине , и при некоторой величине  оказывается больше единицы, электронный газ оказывается релятивистским. Импульс
электрона связан со скоростью известным соотношением
оказывается больше единицы, электронный газ оказывается релятивистским. Импульс
электрона связан со скоростью известным соотношением
 а энергия электрона
а энергия электрона
 При малых
При малых 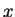 , когда , когда
 , получим уже известную
формулу , получим уже известную
формулу

При  (оставляя только главный член в разложении) энергия одного электрона (оставляя только главный член в разложении) энергия одного электрона
 , следовательно, энергия единицы массы , следовательно, энергия единицы массы
 , а
давление , а
давление
 . .
Таким образом, ультрарелятивистский вырожденный электронный газ подчиняется уравнению
состояния с показателем
 (индекс политропы (индекс политропы 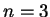 ). ).
Нам уже известно (см. выше), что при 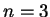 равновесное состояние возможно только
при одной определенной массе. Для вырожденного релятивистского вещества (2.1)
дает это значение массы равновесное состояние возможно только
при одной определенной массе. Для вырожденного релятивистского вещества (2.1)
дает это значение массы
 Для
Для
 . Для всех промежуточных случаев имеются
точные численные расчеты (рис. 16). . Для всех промежуточных случаев имеются
точные численные расчеты (рис. 16).
 |
| Рис. 16. |
Итак, для холодного вещества решение существует только при
 ( (
 -- называют чандрасекаровским пределом массы). Из наблюдений мы знаем,
что есть горячие звезды с массой, большей -- называют чандрасекаровским пределом массы). Из наблюдений мы знаем,
что есть горячие звезды с массой, большей
 . В результате эволюции
при остывании таких звезд должна происходить потеря устойчивости и коллапс (быстрое
сжатие) звезды. . В результате эволюции
при остывании таких звезд должна происходить потеря устойчивости и коллапс (быстрое
сжатие) звезды.
В ньютоновской теории более жесткое уравнение состояния (например, отталкивание
ядер) могло бы спасти звезду от коллапса. Однако в ОТО при любом уравнении состояния
релятивистские эффекты всегда приводят к неустойчивости и неограниченному коллапсу.
Получим, следуя Е.Солпитеру, выражение для предельной массы белого карлика через
фундаментальные физические величины
 , или, другими словами,
найдем предельное число нуклонов , или, другими словами,
найдем предельное число нуклонов
 , для которых гравитация уравновешивается
давлением вырожденных электронов. Имеем , для которых гравитация уравновешивается
давлением вырожденных электронов. Имеем
 . .
Из констант
 и и 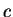 можно составить только одно безразмерное число: можно составить только одно безразмерное число:
 (аналог постоянной тонкой структуры (аналог постоянной тонкой структуры
 ). По определению ). По определению
 безразмерно и безразмерно и
 Как найти
Как найти 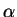 ? Воспользуемся для этого уравнением состояния ультрарелятивистского
вещества и найдем постоянную ? Воспользуемся для этого уравнением состояния ультрарелятивистского
вещества и найдем постоянную 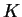 (приближенно) (приближенно)
 т.е.
т.е.
 и и
 . .
Для политропы 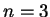 выше мы получили выше мы получили
 . Подставляя . Подставляя 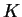 , имеем , имеем
 Окончательно
Окончательно
 Такое большое число обусловлено тем, что константа гравитационного взаимодействия
мала.
Такое большое число обусловлено тем, что константа гравитационного взаимодействия
мала.
<< 2.3 Частные случаи политропных ...
| Оглавление |
2.5 Горячие звезды >>
Посмотреть комментарии[2]
|

