<< 3.4 Тормозное излучение зарядов
| Оглавление |
4. Теория переноса (продолжение) >>
Рассмотрим движение электрона в плоской электромагнитной волне:
 , распространяющейся вдоль оси , распространяющейся вдоль оси  . Уравнение движения электрона: . Уравнение движения электрона:
 и энергия, излучаемая таким электроном,
и энергия, излучаемая таким электроном,
 Своих источников энергии у электрона нет. Фактически он переизлучает (рассеивает)
энергию падающей электромагнитной волны в других направлениях, так что
Своих источников энергии у электрона нет. Фактически он переизлучает (рассеивает)
энергию падающей электромагнитной волны в других направлениях, так что
 эрг эрг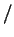 с с![$\displaystyle ],
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img756.gif) где
где
 эрг эрг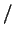 см см![$ ^2]$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img611.gif) -- поток падающей энергии: -- поток падающей энергии:
 и сечение рассеяния
и сечение рассеяния
 см см![$\displaystyle ^2]
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img760.gif) знаменитая формула Томсона. Величина
знаменитая формула Томсона. Величина
 см см называется классическим радиусом электрона.
называется классическим радиусом электрона.
При преобладающей роли электронного рассеяния (процессы поглощения излучения
несущественны) изменение интенсивности 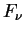 в монохроматическом пучке фотонов,
очевидно, равно в монохроматическом пучке фотонов,
очевидно, равно
 Можно ввести коэффициент ``поглощения'' при томсоновском рассеянии (хотя реально
поглощения энергии и нет):
Можно ввести коэффициент ``поглощения'' при томсоновском рассеянии (хотя реально
поглощения энергии и нет):
 см см где длина пробега
где длина пробега
 см см![$\displaystyle ].
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img741.gif) Интегрируя уравнение для
Интегрируя уравнение для 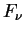 , получаем , получаем
 т.е.
т.е.
 г/см г/см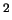 водородной плазмы ( водородной плазмы ( ) уменьшают ) уменьшают 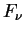 в
в 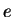 раз за счет электронного рассеяния. раз за счет электронного рассеяния.
В астрофизике обычно пользуются не коэффициентом поглощения
 , а так
называемой непрозрачностью , а так
называемой непрозрачностью
 см см г г![$\displaystyle ].
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img741.gif) Таким образом, непрозрачность за счет рассеяния
Таким образом, непрозрачность за счет рассеяния
 см см г г![$\displaystyle ].
$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img741.gif)
З а д а ч и. 1. Дана водородная ( ) плазма со значениями плотности ) плазма со значениями плотности
 г г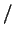 см см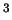 , температурой , температурой
 K. Для K. Для
 найти найти
 . В переменных . В переменных
 найти кривую,
на которой найти кривую,
на которой
 . Подсчитайте . Подсчитайте  . .
2. Пусть в каждой точке звезды плотность и температура связаны соотношением
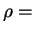 const const , где const заранее не известна. (Тогда , где const заранее не известна. (Тогда
 ,
т.е. индекс политропы ,
т.е. индекс политропы 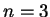 .) Для чисто водородных моделей звезд с массами .) Для чисто водородных моделей звезд с массами
 и центральных плотностей и центральных плотностей
 и и
  найти радиус найти радиус 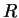 , температуру в центре , температуру в центре 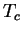 и полную энергию и полную энергию
 . .
3. Пусть распределение плотности по звезде определяется зависимостью
![$ \rho=\rho_c
{[1-(r/R)^2]}^g$](http://images.nature.web.ru/nature/2001/01/18/0001159166/img788.gif) , где , где
 . Найти гравитационную энергию звезды . Найти гравитационную энергию звезды
 , т.е. найти , т.е. найти  . .
Пусть энергия единицы массы 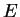 связана с связана с 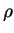 соотношениями: a) соотношениями: a)
 ,
b) ,
b)
 . (Какое при этом . (Какое при этом  ?) ?)
При тех же распределениях плотности найти связь между 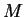 и и  из условия минимума
полной энергии из условия минимума
полной энергии  . .
<< 3.4 Тормозное излучение зарядов
| Оглавление |
4. Теория переноса (продолжение) >>
Посмотреть комментарии[2]
|

