(движение материальных точек
(частиц), притягивающихся по закону Ньютона). Математическое описание
такой системы дается некоторой гамильтоновой системой в 6n-мерном
фазовом пространстве с переменными pi, qi,
i = 1,..., 3n. Здесь
q3i - 2, q3i - 1, q3i суть обычные координаты i-й частицы в
обычном (физическом) пространстве
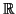 3, а
p3i - 2, p3i - 1, p3i -- проекции ее импульса на координатные
оси в 3, а
p3i - 2, p3i - 1, p3i -- проекции ее импульса на координатные
оси в
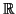 3. Даже не выписывая системы, легко понять, что она
имеет особенности в тех точках, где при каких-нибудь i 3. Даже не выписывая системы, легко понять, что она
имеет особенности в тех точках, где при каких-нибудь i 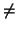 j
координаты i-й частицы совпадают с координатами j-й. Обозначим
через j
координаты i-й частицы совпадают с координатами j-й. Обозначим
через  множество соответствующих точек в конфигурационном
пространстве (пространстве переменных qi); тогда особые точки
системы суть точки множества множество соответствующих точек в конфигурационном
пространстве (пространстве переменных qi); тогда особые точки
системы суть точки множества
 × ×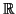 3n. Если
начальные значения
(p(0), q(0)) взяты вне этого множества, то
локально существует соответствующее решение
(p(t), q(t)). Оно не
обязательно продолжается на всю положительную полуось t. Если
максимальный интервал существования решения конечен, скажем, является
интервалом [0, T),
T < 3n. Если
начальные значения
(p(0), q(0)) взяты вне этого множества, то
локально существует соответствующее решение
(p(t), q(t)). Оно не
обязательно продолжается на всю положительную полуось t. Если
максимальный интервал существования решения конечен, скажем, является
интервалом [0, T),
T < 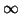 (мы рассматриваем только
положительные t, хотя на самом деле это несущественно), то говорят,
что при t = T у решения имеется особенность. (Вектор-функция
(p(t), q(t)) и впрямь имеет особенность при t = T.) Легко
доказать, что q(t) при t (мы рассматриваем только
положительные t, хотя на самом деле это несущественно), то говорят,
что при t = T у решения имеется особенность. (Вектор-функция
(p(t), q(t)) и впрямь имеет особенность при t = T.) Легко
доказать, что q(t) при t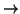 T неограниченно приближается
к T неограниченно приближается
к  . Если существует предел lim q(t) при t . Если существует предел lim q(t) при t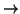 T
(неизбежно принадлежащий T
(неизбежно принадлежащий  ), то говорят, что в системе при
t = T происходит столкновение. (Этимология здесь очевидна: в пределе
при t ), то говорят, что в системе при
t = T происходит столкновение. (Этимология здесь очевидна: в пределе
при t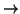 T две или более частиц оказываются в одной и той же точке
физического пространства T две или более частиц оказываются в одной и той же точке
физического пространства
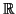 3). До недавнего времени
оставался открытым вопрос, бывают ли особенности, отличные от
столкновений? Известно, что при n 3). До недавнего времени
оставался открытым вопрос, бывают ли особенности, отличные от
столкновений? Известно, что при n 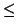 3 таких особенностей нет. Для
n = 2 это просто, а для n = 3 было доказано около 100 лет назад. 3 таких особенностей нет. Для
n = 2 это просто, а для n = 3 было доказано около 100 лет назад.
Если столкновение двойное, то, как обнаружил еще Л.Эйлер, можно
разумным (и вполне наглядным) образом определить дальнейшее движение
системы (в течение некоторого времени) 108.
Эйлеровское доопределение движения после двойного столкновения
увеличивает максимальный интервал существования решения, но (за
исключением случая n = 2) все-таки не обязательно делает его
бесконечным. Так, при n = 3 все может кончиться тройным
столкновением (до которого могут происходить двойные столкновения, но
в течение конечного времени их может произойти только конечное
число) 109.
Перед самым началом последнего 25-летия Дж.Мезер и
Р.Мак-Гехи [158] обнаружили, что уже при n = 4 возможны
особенности иного типа. В их примере за конечное время T происходит
бесконечное число двойных столкновений. Все четыре тела движутся по
одной прямой, причем в итоге при t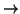 T три тела уходят в
бесконечность -- одно в одну сторону, а два других, неограниченно
сближаясь между собой (что и дает энергию для всего процесса) -- в
другую; четвертое же тело осциллирует между этими двумя, попеременно
сталкиваясь то с одним, то с другим. Возник вопрос, существуют ли
такие особенности, которые не являются столкновениями и которыми
завершается некоторый интервал [0, T), на котором не происходит
столкновений? Здесь уже нельзя обойтись одномерным случаем, что
усложняет задачу. В 1992 г. Дж.Ксиа [159] показал, что при
n T три тела уходят в
бесконечность -- одно в одну сторону, а два других, неограниченно
сближаясь между собой (что и дает энергию для всего процесса) -- в
другую; четвертое же тело осциллирует между этими двумя, попеременно
сталкиваясь то с одним, то с другим. Возник вопрос, существуют ли
такие особенности, которые не являются столкновениями и которыми
завершается некоторый интервал [0, T), на котором не происходит
столкновений? Здесь уже нельзя обойтись одномерным случаем, что
усложняет задачу. В 1992 г. Дж.Ксиа [159] показал, что при
n 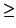 5 подобное явление возможно 110.
Вопрос остается открытым только при n = 4. 111 5 подобное явление возможно 110.
Вопрос остается открытым только при n = 4. 111
Написать комментарий
|

