



Next: 2 евклидово пространство
Up: 1 n-мерное пространство. Линейные
Previous: 1 n-мерное пространство. Линейные
Subsections
Часто приходится встречаться с объектами, над которыми
производятся операции сложения и умножения на числа. Приведем
несколько примеров.
1. В геометрии объектами такого рода являются
векторы в трехмерном пространстве, т.е. направленные отрезки.
При этом, если два направленных отрезка можно совместить
параллельным переносом, то считается, что они определяют один и
тот же вектор. Поэтому удобно все эти отрезки откладывать от
одной какой-либо точки, которую мы будем называть началом
координат. Операция сложения векторов, как известно, определяется
следующим образом: суммой векторов  и и  мы считаем диагональ
параллелограмма со сторонами мы считаем диагональ
параллелограмма со сторонами  и и  . Известным образом
вводится также умножение на числа. . Известным образом
вводится также умножение на числа.
2. В алгебре мы встречаемся с системами  чисел чисел
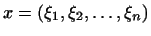 (например, строки матрицы, совокупность
коэффициентов
линейной формы
и т.д.). Для таких
систем операции сложения и умножения на числа обычно определяются так: суммой
систем (например, строки матрицы, совокупность
коэффициентов
линейной формы
и т.д.). Для таких
систем операции сложения и умножения на числа обычно определяются так: суммой
систем
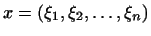 и и
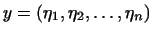 называется система
называется система
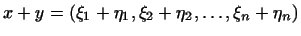 . Произведением
системы . Произведением
системы
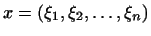 на число на число 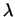 мы считаем
систему мы считаем
систему
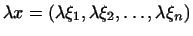 . .
3. В анализе определяются операции сложения функций и
умножения их на числа. В дальнейшем мы для определенности будем
рассматривать совокупность всех непрерывных функций, заданных на
сегменте ![$ [a,b]$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img18.gif) . .
В приведенных примерах одни и те же операции сложения и умножения
на числа производятся над совершенно разными объектами. Для того
чтобы изучить все такие примеры с единой точки зрения, мы введем
понятие линейного, или аффинного, пространства.
Определение 1.1
Множество  элементов элементов
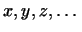 называется
линейным (аффинным) пространством, если: называется
линейным (аффинным) пространством, если:
a) каждым двум элементам  и и  поставлен в соответствие
элемент поставлен в соответствие
элемент 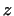 , называемый суммой элементов , называемый суммой элементов  и и  ; сумма
элементов ; сумма
элементов  и и  обозначается через обозначается через 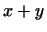 , ,
b) каждому элементу  и каждому числу и каждому числу 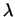 из некоторого
поля
поставлен в соответствие элемент из некоторого
поля
поставлен в соответствие элемент 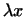 , называемый
произведением элемента , называемый
произведением элемента  на число на число 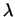 . .
Эти операции должны удовлетворять следующим требованиям
(аксиомам):
I.
1 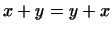 (коммутативность). (коммутативность).
2
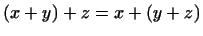 (ассоциативность). (ассоциативность).
3 Существует элемент 0 такой, что Существует элемент 0 такой, что 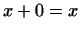 для любого для любого  .
Элемент 0 называется нулевым элементом. .
Элемент 0 называется нулевым элементом.
4 Для каждого Для каждого  существует элемент, обозначаемый через существует элемент, обозначаемый через
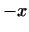 , такой, что , такой, что 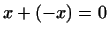 . .
II.
1
 , ,
2
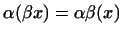 . .
III.
1
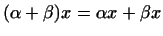 , ,
2
 . .
Мы не случайно не сказали, как именно определяются операции сложения и
умножения на числа. От этих операций требуется только, чтобы были
выполнены сформулированные выше аксиомы. Поэтому всякий раз, когда мы
встречаемся с операциями, удовлетворяющими перечисленным выше
условиям, мы вправе считать их операциями сложения и умножения на
числа, а совокупность элементов, для которых эти операции
установлены,-- линейным пространством.
Предоставляем читателю проверить, что в приведенных примерах 1-3 эти
аксиомы выполнены. Поэтому 1-3 являются примерами линейных
пространств.
Рассмотрим еще несколько примеров.
4. Совокупность всех многочленов степени, не превышающей натурального
числа  , с обычными операциями сложения многочленов и умножения их
на числа образует линейное пространство. , с обычными операциями сложения многочленов и умножения их
на числа образует линейное пространство.
Заметим, что множество многочленов степени  не образует линейного
пространства, так как сумма двух многочленов степени не образует линейного
пространства, так как сумма двух многочленов степени  может
оказаться многочленом более низкой степени: например может
оказаться многочленом более низкой степени: например
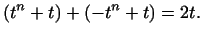
5. Элементами пространства  являются матрицы порядка являются матрицы порядка  .
Суммой матриц .
Суммой матриц
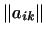 и и
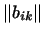 называется матрица называется матрица
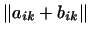 , произведением матрицы , произведением матрицы
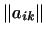 на число на число
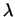 -- матрица -- матрица
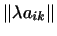 . Нулевым элементом при этом
будет матрица, состоящая из одних нулей. Можно проверить, что все
аксиомы линейного пространства здесь выполнены. . Нулевым элементом при этом
будет матрица, состоящая из одних нулей. Можно проверить, что все
аксиомы линейного пространства здесь выполнены.
6. Совокупность всех многочленов степени, не превышающей натурального
числа  , и имеющих положительные коэффициенты, не образует линейного
пространства: если многочлен , и имеющих положительные коэффициенты, не образует линейного
пространства: если многочлен 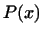 входит в эту совокупность, то входит в эту совокупность, то
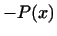 в нее не входит. в нее не входит.
7. Не образует линейного пространства и совокупность
непрерывных функций
на сегменте ![$ [a,b]$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img18.gif) таких,
что таких,
что
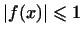 : из того, что : из того, что
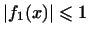 и и
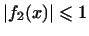 , не следует , не следует
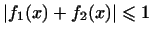 . .
Элементы линейного пространства мы будем называть
векторами.
То обстоятельство, что это слово часто употребляется в более узком
смысле (так, как в примере 1), не должно нас смущать. Геометрические
представления, связанные с этим словом, помогут нам уяснить, а иногда
и предвидеть, ряд результатов.
Если числа
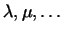 , участвующие в определении линейного
пространства, вещественны, то пространство называется
вещественным линейным пространством. Если же эти числа , участвующие в определении линейного
пространства, вещественны, то пространство называется
вещественным линейным пространством. Если же эти числа
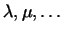 берутся из поля
комплексных чисел,
то берутся из поля
комплексных чисел,
то  называется комплексным линейным пространством. называется комплексным линейным пространством.
Более общо, мы можем предполагать, что
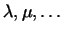 --
элементы произвольного поля --
элементы произвольного поля 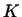 . Тогда . Тогда  называется линейным
пространством над полем называется линейным
пространством над полем 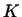 . Многие понятия и теоремы, излагаемые
ниже, в частности, все содержание этого параграфа, автоматически
переносятся на линейные пространства над любым полем.
Однако в главе I мы будем обычно предполагать, что . Многие понятия и теоремы, излагаемые
ниже, в частности, все содержание этого параграфа, автоматически
переносятся на линейные пространства над любым полем.
Однако в главе I мы будем обычно предполагать, что  -- вещественное
линейное пространство.
[chapter] В главе I обычно предполагается, что -- вещественное
линейное пространство.
[chapter] В главе I обычно предполагается, что  -- вещественное
линейное пространство. -- вещественное
линейное пространство.
Важную роль в дальнейшем будет играть понятие линейной зависимости и
линейной независимости векторов.
Определение 1.2
Пусть  -- линейное пространство. Векторы -- линейное пространство. Векторы
 называются
линейно зависимыми,
если существуют такие числа
называются
линейно зависимыми,
если существуют такие числа
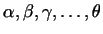 , из которых
хотя бы одно отлично от нуля, что , из которых
хотя бы одно отлично от нуля, что
 |
(1) |
Векторы, не являющиеся линейно зависимыми, называются линейно
независимыми. Другими словами,
векторы
 называются линейно
независимыми, если равенство называются линейно
независимыми, если равенство
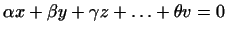 возможно только при
возможно только при
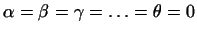 . .
Пусть векторы
 линейно зависимы, т.е. пусть они
связаны соотношением вида (1), в котором хотя бы один из
коэффициентов, например линейно зависимы, т.е. пусть они
связаны соотношением вида (1), в котором хотя бы один из
коэффициентов, например 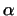 , отличен от нуля. Тогда , отличен от нуля. Тогда
 и, разделив на
и, разделив на 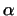 и положив и положив
 получим:
получим:
 |
(2) |
Если вектор  выражается через векторы выражается через векторы
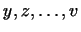 в
виде (2), то мы будем говорить, что в
виде (2), то мы будем говорить, что  есть
линейная комбинация
векторов есть
линейная комбинация
векторов
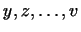 . .
Таким образом, если векторы
 линейно зависимы,
то хотя бы один из них является линейной комбинацией остальных. Мы
предоставляем читателю проверить, что верно и обратное, т.е. что
векторы, один из которых есть линейная комбинация остальных,
линейно зависимы. линейно зависимы,
то хотя бы один из них является линейной комбинацией остальных. Мы
предоставляем читателю проверить, что верно и обратное, т.е. что
векторы, один из которых есть линейная комбинация остальных,
линейно зависимы.
Упражнения
1. Проверить, что если среди векторов
 имеется
нулевой вектор, то эти векторы обязательно линейно зависимы. имеется
нулевой вектор, то эти векторы обязательно линейно зависимы.
2. Показать, что если к линейно зависимым векторам
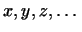 добавить еще произвольные векторы добавить еще произвольные векторы
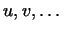 , то
все эти векторы вместе также будут линейно зависимы. , то
все эти векторы вместе также будут линейно зависимы.
3. Доказать, что если векторы
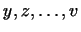 линейно
независимы и вектор линейно
независимы и вектор  есть их линейная комбинация есть их линейная комбинация
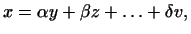 |
(3) |
то представление (3) единственно.
Указание
Предположить, что есть другое представление:
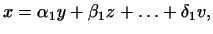 |
(4) |
и вычесть равенство (4) из равенства (3).
Перейдем теперь к определению понятия
числа измерений (размерности) пространства.
В совокупности векторов на прямой всякие два вектора пропорциональны,
т.е. линейно зависимы. На плоскости можно найти два линейно
независимых вектора, но уже всякие три вектора линейно зависимы. Если
 -- совокупность векторов трехмерного пространства, то три линейно
независимых вектора в -- совокупность векторов трехмерного пространства, то три линейно
независимых вектора в  найти можно, но всякие четыре вектора
линейно зависимы. найти можно, но всякие четыре вектора
линейно зависимы.
Мы видим, что максимальное число линейно независимых векторов на
прямой, плоскости, в трехмерном пространстве совпадает с тем, что в
геометрии принято называть числом измерений прямой, плоскости,
пространства. Естественно поэтому следующее общее
Определение 1.3
Линейное пространство  называется называется  -мерным, если в нем существует -мерным, если в нем существует
 линейно независимых векторов и нет большего числа линейно
независимых векторов. линейно независимых векторов и нет большего числа линейно
независимых векторов.
Если в пространстве  можно найти любое число линейно независимых
векторов, то можно найти любое число линейно независимых
векторов, то  называется бесконечномерным. называется бесконечномерным.
Бесконечномерные пространства составляют предмет специального
изучения. Мы будем в этой книге заниматься в основном пространствами
конечного числа измерений.
[document] В этой книге в основном рассматриваются пространства
конечного числа измерений.
Найдем в каждом из рассмотренных выше примеров 1-5 размерность
соответствующего пространства.
1. Как мы уже указали, в пространстве  примера 1 имеется три
линейно независимых вектора, а всякие четыре вектора линейно
зависимы. Поэтому примера 1 имеется три
линейно независимых вектора, а всякие четыре вектора линейно
зависимы. Поэтому  трехмерно. трехмерно.
2.  -- пространство, векторами которого являются системы -- пространство, векторами которого являются системы  действительных чисел.
действительных чисел.
В этом пространстве можно указать  линейно независимых векторов,
например линейно независимых векторов,
например
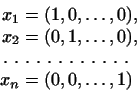 (мы предоставляем читателю доказать, что эти векторы действительно
линейно независимы).
(мы предоставляем читателю доказать, что эти векторы действительно
линейно независимы).
Упражнение
Показать, что векторы
 в пространстве
в пространстве  также линейно независимы также линейно независимы
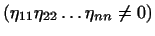 . .
3.  -- пространство непрерывных функций. Пусть -- пространство непрерывных функций. Пусть 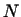 --
произвольное целое число. Тогда функции --
произвольное целое число. Тогда функции
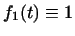 , ,
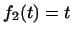 , , 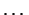 , ,
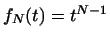 образуют совокупность образуют совокупность 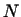 линейно независимых векторов (доказательство предоставляем
читателю). Мы видим, что в этом пространстве имеется произвольное
число линейно независимых функций, т.е.
линейно независимых векторов (доказательство предоставляем
читателю). Мы видим, что в этом пространстве имеется произвольное
число линейно независимых функций, т.е.  бесконечномерно. бесконечномерно.
4.  -- пространство многочленов степени -- пространство многочленов степени
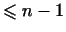 . В нем . В нем
 многочленов многочленов
 линейно независимы. линейно независимы.
5. В пространстве квадратных матриц
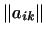 порядка порядка  все
матрицы, у которых на одном каком-либо месте стоит единица, а на
остальных местах нули, линейно независимы. все
матрицы, у которых на одном каком-либо месте стоит единица, а на
остальных местах нули, линейно независимы.
В примерах 1, 2, 4 и 5 мы нашли систему таких линейно независимых
векторов
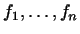 , что каждый вектор , что каждый вектор 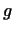 есть их линейная
комбинация. Чтобы установить, что размерность каждого из этих
пространств равна числу векторов есть их линейная
комбинация. Чтобы установить, что размерность каждого из этих
пространств равна числу векторов
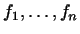 , нам остается
доказать, что в этих пространствах нельзя найти другой системы линейно
независимых векторов , нам остается
доказать, что в этих пространствах нельзя найти другой системы линейно
независимых векторов
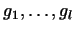 в количестве,
превосходящем в количестве,
превосходящем  . Этот факт можно вывести из следующей полезной
леммы, которой мы неоднократно будем пользоваться и в дальнейшем. . Этот факт можно вывести из следующей полезной
леммы, которой мы неоднократно будем пользоваться и в дальнейшем.
Лемма
Пусть в линейном пространстве задана система из векторов
 Пусть, далее, каждый из векторов
Пусть, далее, каждый из векторов
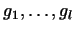 есть линейная комбинация векторов
есть линейная комбинация векторов
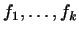 . Тогда,
если векторы . Тогда,
если векторы
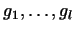 линейно независимы, то линейно независимы, то
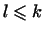 . .
Другими словами, среди линейных комбинаций  векторов векторов
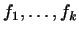 не может быть больше чем
не может быть больше чем  линейно независимых. линейно независимых.
Доказательство леммы проведем по
индукции.
При 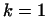 она
очевидна. Предположим, что лемма верна для она
очевидна. Предположим, что лемма верна для 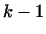 векторов векторов
 , и докажем при этом, что она верна для , и докажем при этом, что она верна для
 векторов. векторов.
Итак, пусть среди линейных комбинаций векторов
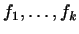 есть линейно независимые векторы
есть линейно независимые векторы
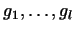 : :
Нам надо показать, что
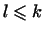 . Если все коэффициенты при . Если все коэффициенты при 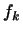 равны нулю, лемма доказана, так как в этом случае, по предположению
индукции, имеет место равенство
равны нулю, лемма доказана, так как в этом случае, по предположению
индукции, имеет место равенство
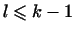 , а значит, и подавно, , а значит, и подавно,
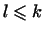 . Пусть хотя бы один из коэффициентов при . Пусть хотя бы один из коэффициентов при 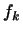 ,
например ,
например
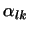 , не равен нулю. Чтобы провести индукцию, мы
построим , не равен нулю. Чтобы провести индукцию, мы
построим 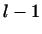 новых линейно независимых векторов, которые будут
линейными комбинациями векторов новых линейно независимых векторов, которые будут
линейными комбинациями векторов
 . Для этого из
последнего равенства выразим . Для этого из
последнего равенства выразим 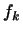 : :
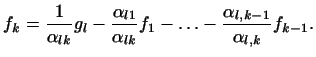 Это выражение для
Это выражение для 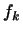 подставим теперь в каждое из первых подставим теперь в каждое из первых 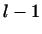 равенств (5) и соберем подобные члены. Мы получим
равенства следующего вида:
равенств (5) и соберем подобные члены. Мы получим
равенства следующего вида:
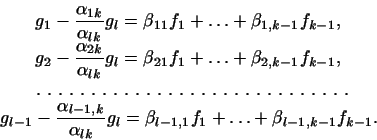 |
(6) |
Эти равенства означают, что каждый из 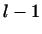 векторов векторов
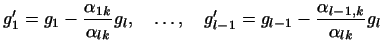 есть линейная комбинация векторов
есть линейная комбинация векторов
 . Если
мы докажем, что они линейно независимы, то, по предположению
индукции, отсюда будет следовать, что . Если
мы докажем, что они линейно независимы, то, по предположению
индукции, отсюда будет следовать, что
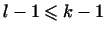 , т.е. , т.е.
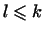 . .
Таким образом, нам осталось показать, что векторы
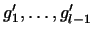 линейно независимы. Но это почти очевидно. Действительно,
предположим, что линейно независимы. Но это почти очевидно. Действительно,
предположим, что
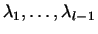 -- такие числа,
что -- такие числа,
что
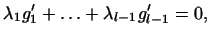 т.е. что
т.е. что
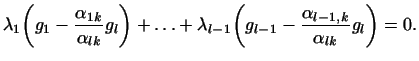 Раскрывая скобки, получаем:
Раскрывая скобки, получаем:
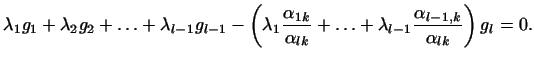 Так как векторы
Так как векторы
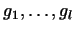 линейно независимы, то все
коэффициенты в последнем равенстве равны нулю. В частности, линейно независимы, то все
коэффициенты в последнем равенстве равны нулю. В частности,
 , а это означает, что
векторы , а это означает, что
векторы
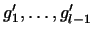 линейно независимы. Лемма полностью
доказана. линейно независимы. Лемма полностью
доказана.
Из доказанной леммы вытекает следующий, часто оказывающийся
полезным результат: если в пространстве  существуют
существуют  линейно независимых векторов линейно независимых векторов
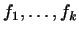 таких, что каждый вектор из
таких, что каждый вектор из  есть их линейная комбинация, то
пространство есть их линейная комбинация, то
пространство   -мерно. -мерно.
Доказательство этого факта ввиду его простоты мы оставляем читателю.
В каждом из примеров 2, 4 и 5 такая система была выбрана. Таким
образом показано, что в примерах 2 и 4 размерность пространства
равна  , а в примере 5 размерность пространства равна , а в примере 5 размерность пространства равна  . .
Упражнение
Показать, что если векторы
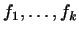 ,
входящие в условие леммы, линейно зависимы, то ,
входящие в условие леммы, линейно зависимы, то 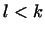 (а не только (а не только
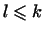 ). ).
Определение 1.4
Совокупность  линейно независимых векторов линейно независимых векторов
  -мерного пространства -мерного пространства  называется
базисом в называется
базисом в  . .
Например, в пространстве  , рассмотренном в примере 1 (трехмерном
пространстве), базис образуют любые три вектора, не лежащие в одной
плоскости. , рассмотренном в примере 1 (трехмерном
пространстве), базис образуют любые три вектора, не лежащие в одной
плоскости.
По определению  -мерного пространства в нем существует -мерного пространства в нем существует  линейно
независимых векторов, т.е. существует базис. линейно
независимых векторов, т.е. существует базис.
Покажем, что произвольную систему из  линейно независимых
векторов линейно независимых
векторов
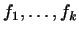 , где , где 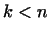 , можно дополнить до
базиса в , можно дополнить до
базиса в  -мерном пространстве -мерном пространстве  . .
Пусть
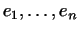 -- какой-либо базис в -- какой-либо базис в  . Если бы каждый из
векторов . Если бы каждый из
векторов
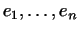 был линейной комбинацией векторов был линейной комбинацией векторов  ,
то, согласно лемме, мы имели бы, что ,
то, согласно лемме, мы имели бы, что
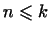 , в то время как,
по предположению, , в то время как,
по предположению, 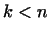 . Значит, среди векторов . Значит, среди векторов
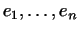 есть
хотя бы один, например есть
хотя бы один, например 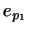 , не являющийся линейной комбинацией
векторов , не являющийся линейной комбинацией
векторов
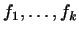 . Добавив вектор . Добавив вектор 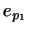 к к
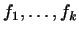 , мы получим систему из , мы получим систему из  векторов, которые
по-прежнему линейно независимы (почему?). векторов, которые
по-прежнему линейно независимы (почему?).
Если 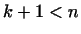 , то среди векторов , то среди векторов
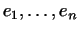 снова есть
вектор снова есть
вектор 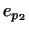 , не являющийся линейной комбинацией векторов , не являющийся линейной комбинацией векторов
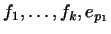 . Добавим и этот вектор к системе.
Этот процесс можно продолжить до тех пор, пока мы дойдем до . Добавим и этот вектор к системе.
Этот процесс можно продолжить до тех пор, пока мы дойдем до  линейно независимых векторов, т.е. до базиса. Этот базис
содержит
линейно независимых векторов, т.е. до базиса. Этот базис
содержит
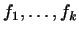 , и тем самым наше утверждение
доказано. , и тем самым наше утверждение
доказано.
Теорема 1.1
Каждый вектор  из из  -мерного пространства -мерного пространства  можно представить, и
при том единственным образом, как линейную комбинацию векторов базиса. можно представить, и
при том единственным образом, как линейную комбинацию векторов базиса.
Доказательство. Пусть векторы
 образуют
базис в образуют
базис в  . Присоединим к ним произвольный вектор . Присоединим к ним произвольный вектор  из из  .
Векторов .
Векторов
 уже уже 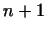 .
Поэтому по определению .
Поэтому по определению  -мерного пространства они должны быть
линейно зависимы, т.е. -мерного пространства они должны быть
линейно зависимы, т.е.
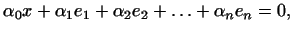 |
(7) |
где не все 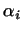 равны нулю. Число равны нулю. Число 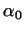 заведомо
отлично от нуля, так как иначе из формулы (7) следовала бы
линейная зависимость векторов заведомо
отлично от нуля, так как иначе из формулы (7) следовала бы
линейная зависимость векторов
 . .
Выразим из (7) вектор  : :
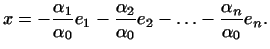 Мы доказали, что каждый вектор
Мы доказали, что каждый вектор 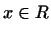 2.1 есть линейная
комбинация векторов 2.1 есть линейная
комбинация векторов
 . .
Докажем теперь единственность полученного разложения.
Предположим, что существуют два разложения:
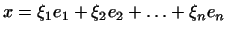 и
и
 Вычитая, получим:
Вычитая, получим:
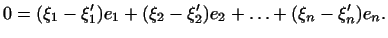 Так как
Так как
 линейно независимы, то это
возможно лишь, если линейно независимы, то это
возможно лишь, если
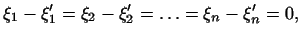 т.е.
т.е.
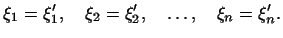 Единственность разложения доказана.
Единственность разложения доказана.
Определение 1.5
Если
 есть базис в есть базис в  -мерном пространстве и -мерном пространстве и
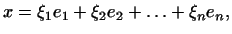 |
(8) |
то числа
 называются
координатами вектора называются
координатами вектора  в базисе в базисе
 . .
Теорема 1 означает, что при заданном базисе
 каждый вектор имеет координаты и притом однозначно определенные. каждый вектор имеет координаты и притом однозначно определенные.
Если вектор  имеет в базисе имеет в базисе
 координаты
координаты
 , а вектор , а вектор
 -- координаты -- координаты
 , т.е.
если , т.е.
если
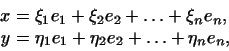 то
то
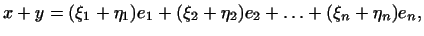 т.е. вектор
т.е. вектор 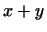 имеет координаты имеет координаты
 . Вектор . Вектор 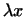 имеет координаты имеет координаты
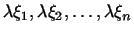 . .
Таким образом, при сложении векторов  и и  их координаты
складываются. При умножении вектора их координаты
складываются. При умножении вектора  на число на число 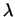 его
координаты умножаются на это число. его
координаты умножаются на это число.
Ясно также, что нулевой вектор, и только он, имеет все координаты
равными нулю.
Примеры
1. Для случая трехмерного пространства наше определение координат
вектора совпадает с имеющимся в
аналитической геометрии
определением координат вектора в некоторой (вообще говоря, не прямоугольной)
системе координат.
2. Пусть  -- пространство, векторами которого
являются системы -- пространство, векторами которого
являются системы
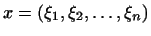 из из  чисел. Возьмем
базис (см. упражнение) чисел. Возьмем
базис (см. упражнение)
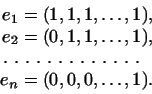
Найдем координаты
 вектора вектора
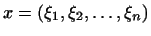 в этом базисе. По
определению в этом базисе. По
определению
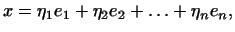 т.е.
т.е.
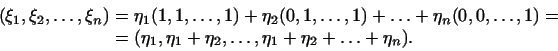 Таким образом, числа
Таким образом, числа
 находятся из
следующей системы уравнений: находятся из
следующей системы уравнений:
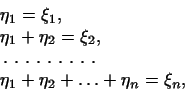 откуда
откуда
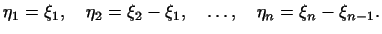
Рассмотрим теперь в  базис, в котором связь между координатами
вектора базис, в котором связь между координатами
вектора
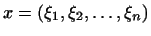 и числами и числами 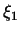 , ,
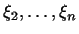 , определяющими этот вектор, наиболее проста. Пусть , определяющими этот вектор, наиболее проста. Пусть
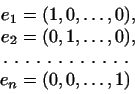 Тогда
Тогда
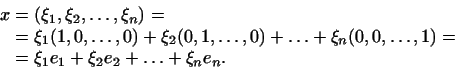 Таким образом, в пространстве
Таким образом, в пространстве  , где каждый вектор
определяется как система , где каждый вектор
определяется как система  чисел чисел
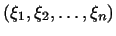 , эти
числа можно трактовать как координаты вектора , эти
числа можно трактовать как координаты вектора
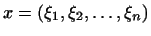 в базисе в базисе
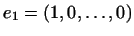 , ,
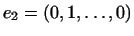 , , 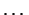 , ,
 . .
Упражнение
Доказать, что в любом базисе
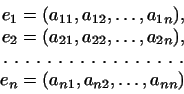 координаты
координаты
 вектора вектора
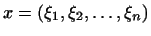 суть линейные комбинации чисел суть линейные комбинации чисел
 . .
3.  -- пространство, векторами которого являются многочлены степени -- пространство, векторами которого являются многочлены степени
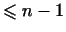 . Простейшим базисом является совокупность векторов . Простейшим базисом является совокупность векторов 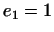 , ,
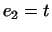 , , 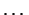 , ,
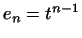 . Координатами многочлена . Координатами многочлена
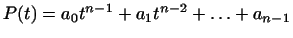 в этом базисе являются, как легко
видеть, его коэффициенты в этом базисе являются, как легко
видеть, его коэффициенты
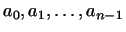 . .
Выберем теперь другой базис:
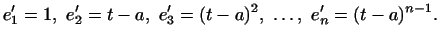 Каждый многочлен
Каждый многочлен 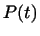 может быть по
формуле Тейлора
представлен в виде: может быть по
формуле Тейлора
представлен в виде:
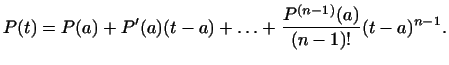 Таким образом, в этом базисе
Таким образом, в этом базисе 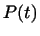 имеет координаты имеет координаты
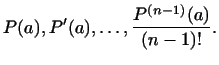
В разобранных выше примерах некоторые пространства с точки зрения
рассматриваемых здесь свойств не отличаются друг от друга. Таковы,
например, обычное трехмерное пространство  примера 1 и пространство примера 1 и пространство
 , в котором векторы определяются как тройки действительных
чисел. В самом деле, выбрав в , в котором векторы определяются как тройки действительных
чисел. В самом деле, выбрав в  определенную систему координат, мы
можем каждому вектору из определенную систему координат, мы
можем каждому вектору из  поставить в соответствие совокупность
трех его координат, т.е. вектор пространства поставить в соответствие совокупность
трех его координат, т.е. вектор пространства  . При сложении
векторов координаты их складываются, а при умножении на число все
координаты вектора умножаются на это число. Поэтому геометрические
факты, вытекающие из определения линейного пространства, которые имеют
место в . При сложении
векторов координаты их складываются, а при умножении на число все
координаты вектора умножаются на это число. Поэтому геометрические
факты, вытекающие из определения линейного пространства, которые имеют
место в  , мы можем параллельно изложить как в , мы можем параллельно изложить как в  , так и в
пространстве , так и в
пространстве  троек чисел. троек чисел.
Поскольку единственными операциями, которые введены в линейных
пространствах, являются операции сложения векторов и умножения
вектора на число, то естественно ввести следующее
Определение 1.6
Линейные пространства  и и  называются
изоморфными,
если между векторами называются
изоморфными,
если между векторами 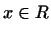 и векторами и векторами 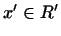 можно установить
взаимно однозначное соответствие 2.2 можно установить
взаимно однозначное соответствие 2.2
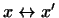 так, что если вектору так, что если вектору  соответствует вектор соответствует вектор
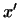 , а вектору , а вектору  соответствует вектор соответствует вектор 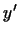 , то , то
1 вектору вектору 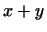 соответствует вектор соответствует вектор 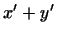 , ,
2 вектору вектору 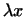 соответствует вектор соответствует вектор
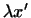 . .
Из определения изоморфизма следует, что если
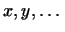 -- векторы
из -- векторы
из  , а , а
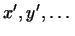 -- соответствующие им векторы из -- соответствующие им векторы из  , то
равенство , то
равенство
 равносильно равенству равносильно равенству
 . Следовательно, линейно независимым векторам из . Следовательно, линейно независимым векторам из
 соответствуют линейно независимые векторы из соответствуют линейно независимые векторы из  , и обратно. , и обратно.
Возникает вопрос, какие пространства изоморфны между собой и
какие нет.
Два пространства различной размерности заведомо не изоморфны
друг другу.
В самом деле, пусть  и и  изоморфны. Из сделанного выше
замечания следует, что максимальное число линейно независимых
векторов в изоморфны. Из сделанного выше
замечания следует, что максимальное число линейно независимых
векторов в  и и  одно и то же, т.е. размерности
пространств одно и то же, т.е. размерности
пространств  и и  равны. Следовательно, пространства
различной размерности не могут быть между собой изоморфны. равны. Следовательно, пространства
различной размерности не могут быть между собой изоморфны.
Теорема 1.2
Все пространства, имеющие одну и ту же размерность  , изоморфны друг
другу. , изоморфны друг
другу.
Доказательство. Пусть  и и  -- два -- два  -мерных пространства.
Выберем в -мерных пространства.
Выберем в  базис базис
 и в и в  какой-либо базис
какой-либо базис
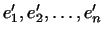 . Поставим в
соответствие вектору . Поставим в
соответствие вектору
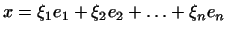 |
(9) |
вектор
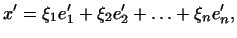 т.е. линейную комбинацию векторов
т.е. линейную комбинацию векторов 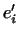 с теми же
коэффициентами, что и в (9). с теми же
коэффициентами, что и в (9).
Это соответствие взаимно однозначно. В самом деле, каждый вектор
 может быть однозначно представлен в виде (9). Поэтому
числа может быть однозначно представлен в виде (9). Поэтому
числа 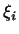 , а значит, и вектор , а значит, и вектор 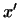 , определяются по вектору , определяются по вектору
 однозначно. Ввиду равноправности, в нашем построении,
пространств однозначно. Ввиду равноправности, в нашем построении,
пространств  и и  , каждому , каждому 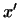 отвечает элемент из отвечает элемент из  и
притом только один. и
притом только один.
Из установленного закона соответствия сразу следует, что если
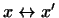 и и
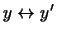 , то , то
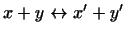 и и
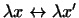 . Изоморфизм пространств . Изоморфизм пространств
 и и  , таким образом, доказан. , таким образом, доказан.
Итак, единственной существенной характеристикой конечномерного
линейного пространства является его размерность.
В 3 мы еще вернемся к понятию изоморфизма
по другому поводу.
Определение 1.7
Подпространством
 пространства пространства  называется совокупность элементов из называется совокупность элементов из  таких,
что они сами образуют линейное пространство относительно уже введенных
в таких,
что они сами образуют линейное пространство относительно уже введенных
в  операций сложения и умножения на числа. операций сложения и умножения на числа.
Иначе говоря, совокупность  элементов элементов
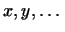 из из  образует линейное подпространство пространства
образует линейное подпространство пространства  , если из , если из 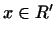 , ,
 следует следует 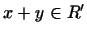 , ,
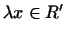 . .
Примеры
1. Нулевое подпространство, т.е. подпространство, состоящее из
единственного элемента -- нуля.
2. Все пространство  . .
Нулевое подпространство и все пространство называются обычно
несобственными подпространствами. Приведем несколько более
содержательных примеров подпространств.
3.  -- трехмерное пространство. Рассмотрим какую-либо
плоскость в -- трехмерное пространство. Рассмотрим какую-либо
плоскость в  , проходящую через начало координат. Совокупность , проходящую через начало координат. Совокупность
 всех векторов, лежащих в этой плоскости, есть
подпространство. всех векторов, лежащих в этой плоскости, есть
подпространство.
4. В пространстве, векторами которого являются системы  чисел чисел
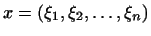 , совокупность всех тех
векторов , совокупность всех тех
векторов
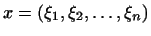 , для которых , для которых
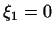 , образует подпространство. Более общо: совокупность
векторов , образует подпространство. Более общо: совокупность
векторов
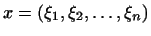 , удовлетворяющих
условию , удовлетворяющих
условию
 где
где
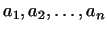 -- какие-то фиксированные числа,
образует подпространство. -- какие-то фиксированные числа,
образует подпространство.
5. В пространстве всех непрерывных функций совокупность
многочленов степени
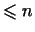 является подпространством. является подпространством.
Очевидно, что во всяком подпространстве  какого-либо
пространства какого-либо
пространства  содержится нулевой элемент пространства содержится нулевой элемент пространства  . .
Поскольку любое подпространство само по себе является линейным
пространством, то все такие понятия, как базис, число измерений
пространства и т.д., которые мы ввели выше, применимы и к
подпространствам. Так как в подпространстве не может быть больше
линейно независимых векторов, чем во всем пространстве, то
размерность любого подпространства не превосходит размерности
всего пространства.
Упражнения
1. Доказать, что если подпространство  пространства пространства  имеет ту
же размерность, что и все пространство имеет ту
же размерность, что и все пространство  , то оно совпадает с , то оно совпадает с  . .
2. Доказать, что если  и и  -- подпространства пространства -- подпространства пространства
 , и если , и если
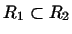 и размерности и размерности  и и  совпадают, то совпадают, то
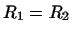 . .
В каждом пространстве  можно строить подпространства следующим
общим приемом: возьмем в можно строить подпространства следующим
общим приемом: возьмем в  произвольное (конечное или бесконечное)
множество векторов произвольное (конечное или бесконечное)
множество векторов
 ; тогда совокупность ; тогда совокупность  всех линейных комбинаций выбранных векторов
всех линейных комбинаций выбранных векторов
 есть
подпространство пространства есть
подпространство пространства  . Действительно, складывая между
собой и умножая на числа линейные комбинации векторов . Действительно, складывая между
собой и умножая на числа линейные комбинации векторов
 , мы снова получим линейные комбинации векторов , мы снова получим линейные комбинации векторов
 , т.е. элементы из , т.е. элементы из  . Полученное таким образом
подпространство . Полученное таким образом
подпространство  называется подпространством, порожденным
векторами называется подпространством, порожденным
векторами
 . Оно является наименьшим линейным
подпространством, содержащим данные векторы . Оно является наименьшим линейным
подпространством, содержащим данные векторы

Подпространство  , порожденное линейно независимыми векторами , порожденное линейно независимыми векторами
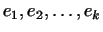 , является , является  -мерным и векторы -мерным и векторы
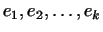 образуют в нем базис. Действительно, в образуют в нем базис. Действительно, в  имеется система имеется система  линейно независимых векторов, именно, сами векторы
линейно независимых векторов, именно, сами векторы
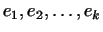 . С другой стороны, если . С другой стороны, если
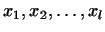 -- произвольные
линейно независимые векторы из -- произвольные
линейно независимые векторы из  , то так как они являются линейными
комбинациями векторов , то так как они являются линейными
комбинациями векторов
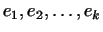 , то, согласно
лемме п.2, , то, согласно
лемме п.2,
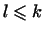 . Следовательно, . Следовательно,   -мерно и набор векторов -мерно и набор векторов
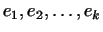 есть один из
возможных базисов в есть один из
возможных базисов в  . .
Упражнение
Показать, что в  -мерном пространстве существуют подпространства
всех меньших размерностей. -мерном пространстве существуют подпространства
всех меньших размерностей.
Если исключить из рассмотрения не представляющее интереса нулевое
подпространство, то самыми простыми являются одномерные
подпространства. Базис всякого такого подпространства состоит из
одного вектора 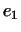 . Таким образом, одномерное подпространство
состоит из векторов вида . Таким образом, одномерное подпространство
состоит из векторов вида
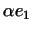 , где , где 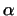 -- произвольное
число. -- произвольное
число.
Прибавим к каждому из векторов
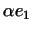 один и тот же
вектор один и тот же
вектор 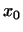 . Мы получим совокупность векторов вида . Мы получим совокупность векторов вида
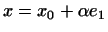 , где , где 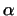 пробегает все числа, а пробегает все числа, а 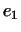 и и 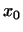 --
фиксированные векторы. Эту совокупность векторов естественно, по
аналогии с трехмерным пространством, назвать прямой в линейном
пространстве --
фиксированные векторы. Эту совокупность векторов естественно, по
аналогии с трехмерным пространством, назвать прямой в линейном
пространстве  . .
Аналогично, векторы вида
 , где , где 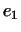 и и 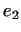 --
фиксированные линейно независимые векторы, а --
фиксированные линейно независимые векторы, а 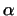 и и  --
произвольные числа, образуют двумерное подпространство. Совокупность
векторов --
произвольные числа, образуют двумерное подпространство. Совокупность
векторов
 где
где 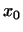 -- фиксированный вектор, мы называем плоскостью
(двумерной). -- фиксированный вектор, мы называем плоскостью
(двумерной).
Упражнения
1. Показать, что в пространстве, где векторами являются системы  действительных чисел
действительных чисел
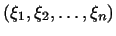 , совокупность
векторов, удовлетворяющих соотношению , совокупность
векторов, удовлетворяющих соотношению
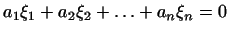 (
(
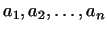 -- фиксированные числа, не все равные нулю),
образует подпространство размерности -- фиксированные числа, не все равные нулю),
образует подпространство размерности 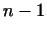 . .
2. Показать, что если два подпространства  и и  пространства пространства
 имеют общим лишь нулевой вектор, то сумма их размерностей не
превосходит размерности имеют общим лишь нулевой вектор, то сумма их размерностей не
превосходит размерности  . .
3. Показать, что размерность подпространства, порожденного векторами
 , равна максимальному числу линейно независимых
векторов среди них. , равна максимальному числу линейно независимых
векторов среди них.
6 Разложение пространства в прямую сумму
подпространств. Сумма и пересечение подпространств.
Пусть заданы два подпространства  -мерного
пространства -мерного
пространства  . Обозначим их . Обозначим их  и и  . .
Определение 1.8
Если каждый вектор  пространства пространства  можно, и притом единственным
образом, представить как сумму двух векторов можно, и притом единственным
образом, представить как сумму двух векторов
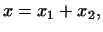 где
где
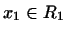 , а , а
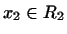 , то говорят, что пространство , то говорят, что пространство  разложено в
прямую сумму подпространств
разложено в
прямую сумму подпространств
 и и  . .
Это обычно записывают так:
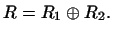
Теорема 1.3
Для того чтобы пространство  разлагалось в прямую сумму
подпространств разлагалось в прямую сумму
подпространств  и и  , достаточно, чтобы: , достаточно, чтобы:
1. Подпространства  и и  имели только один общий вектор имели только один общий вектор
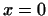 (нулевой вектор). (нулевой вектор).
2. Сумма размерностей этих подпространств была равна размерности
пространства  . .
Доказательство. Выберем некоторый базис
 в подпространстве в подпространстве  и
базис и
базис
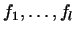 в подпространстве в подпространстве  . Поскольку сумма
размерностей . Поскольку сумма
размерностей  и и  есть есть  , то общее число этих векторов , то общее число этих векторов
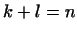 . .
Покажем, что векторы
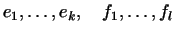 линейно независимы, т.е. образуют базис пространства
линейно независимы, т.е. образуют базис пространства  .
Действительно, пусть .
Действительно, пусть
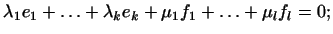 отсюда
отсюда
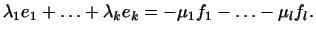 Левая часть этого равенства есть вектор из
Левая часть этого равенства есть вектор из  , а правая из , а правая из  .
Так как, по условию, единственный общий вектор .
Так как, по условию, единственный общий вектор  и и  есть
нулевой вектор, то есть
нулевой вектор, то
Но каждый из наборов
 и и
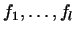 состоит из линейно независимых векторов, так как это базисы в
состоит из линейно независимых векторов, так как это базисы в  и
и  . Поэтому из первого равенства (10) следует, что . Поэтому из первого равенства (10) следует, что
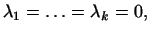 а из второго следует, что
а из второго следует, что

Следовательно, система
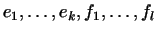 состоит из состоит из
 линейно независимых векторов, т.е. это есть базис в пространстве линейно независимых векторов, т.е. это есть базис в пространстве
 . .
Мы доказали, что при выполнении условий теоремы существует базис,
первые  векторов которого образуют базис в векторов которого образуют базис в  , а последние , а последние 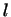 -- базис в
-- базис в  . .
Произвольный вектор  из из  можно разложить по векторам этого
базиса можно разложить по векторам этого
базиса
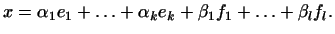 При этом
При этом
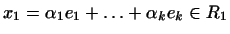 и
и
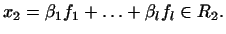 Таким образом,
Таким образом,
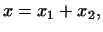 где
где
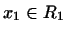 и и
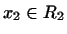 . Покажем, что это разложение
единственно. Предположим, что существуют два разложения: . Покажем, что это разложение
единственно. Предположим, что существуют два разложения:
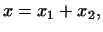 где где и
и
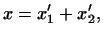 где где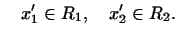
Вычитая второе равенство из первого, получаем:
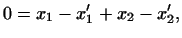 откуда
откуда

Так как вектор, стоящий в левой части равенства, принадлежит  , а
вектор, стоящий в правой части, принадлежит , а
вектор, стоящий в правой части, принадлежит  , то каждый из этих
векторов равен нулю, т.е. , то каждый из этих
векторов равен нулю, т.е.
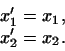
Единственность разложения доказана.
Допустим, что нам задано два произвольных подпространства  и
и  линейного пространства линейного пространства  . .
Легко проверить, что совокупность векторов, принадлежащих обоим этим
подпространствам, также есть подпространство 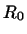 пространства пространства  . .
Это подпространство называется
пересечением
 и и  и обозначается
и обозначается
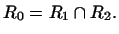
Например, если  и и  -- два двумерных подпространства
трехмерного пространства (две плоскости, проходящие через начало
координат), то -- два двумерных подпространства
трехмерного пространства (две плоскости, проходящие через начало
координат), то
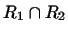 есть одномерное подпространство (прямая,
по которой пересекаются эти плоскости). есть одномерное подпространство (прямая,
по которой пересекаются эти плоскости).
По двум подпространствам  и и  можно построить еще одно
подпространство, которое называется их суммой. Оно
определяется следующим образом. можно построить еще одно
подпространство, которое называется их суммой. Оно
определяется следующим образом.
Векторами этого подпространства являются всевозможные суммы вида
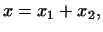 |
(11) |
где
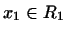 , ,
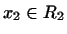 . .
Легко проверить, что элементы вида (11) образуют подпространство. Это
подпространство 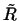 называется суммой подпространств называется суммой подпространств  и
и  и обозначается и обозначается
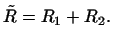
Заметим, что, в отличие от прямой суммы двух подпространств, запись
элемента из  в виде (11) может быть неоднозначной. в виде (11) может быть неоднозначной.
Упражнение
Показать, что сумма двух различных двумерных
подпространств трехмерного пространства  есть все это пространство. есть все это пространство.
Имеет место следующая теорема:
Теорема 1.4
Пусть заданы два подпространства  и и  пространства пространства  .
Тогда сумма размерностей .
Тогда сумма размерностей  и и  равна размерности их суммы плюс
размерность пересечения. равна размерности их суммы плюс
размерность пересечения.
Доказательство. Выберем в пересечении
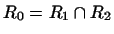 базис базис
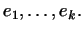 |
(12) |
Дополним этот базис с одной стороны до базиса в  : :
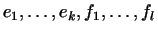 |
(13) |
и с другой стороны до базиса в  : :
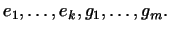 |
(14) |
Покажем, что векторы
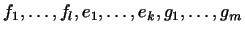 |
(15) |
образуют базис в сумме
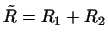 . .
Сначала покажем, что эти векторы линейно независимы. Действительно,
пусть
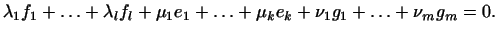 Тогда
Тогда
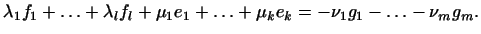 Левая часть этого равенства есть вектор из
Левая часть этого равенства есть вектор из  , правая -- из , правая -- из
 . Таким образом, эта правая часть есть одновременно вектор из . Таким образом, эта правая часть есть одновременно вектор из
 и из и из  , т.е. принадлежит , т.е. принадлежит 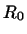 и, значит, выражается как
линейная комбинация базиса и, значит, выражается как
линейная комбинация базиса
 подпространства подпространства 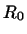 : :
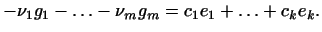
В силу линейной независимости векторов (14) это возможно только,
когда все коэффициенты -- нули. В частности,
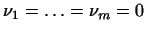 , т.е. , т.е.
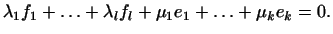
Из линейной независимости векторов (13) получаем, что и все
коэффициенты
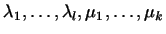 равны нулю. Таким образом, линейная независимость
системы (15) доказана. равны нулю. Таким образом, линейная независимость
системы (15) доказана.
Покажем теперь, что всякий вектор
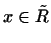 выражается как
линейная комбинация векторов этой системы. По определению выражается как
линейная комбинация векторов этой системы. По определению 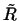 вектор
вектор  можно представить в виде: можно представить в виде:
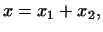 где
где
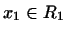 , ,
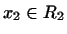 . Так как . Так как
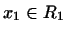 , то его можно
представить как линейную комбинацию векторов (13). Аналогично , то его можно
представить как линейную комбинацию векторов (13). Аналогично
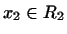 и и 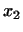 можно представить как линейную комбинацию векторов (14).
Складывая, получим, что вектор можно представить как линейную комбинацию векторов (14).
Складывая, получим, что вектор  представим как линейная комбинация
системы (15). представим как линейная комбинация
системы (15).
Итак мы получили, что векторы
 с одной стороны, линейно независимы и, с другой стороны, всякий
вектор из
с одной стороны, линейно независимы и, с другой стороны, всякий
вектор из 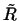 есть их линейная комбинация. В силу
замечания на стр. есть их линейная комбинация. В силу
замечания на стр.![[*]](http://images.nature.web.ru/nature/2000/10/02/0001151602/crossref.png) отсюда следует, что эти векторы
образуют базис в отсюда следует, что эти векторы
образуют базис в 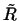 . Итак, мы имеем . Итак, мы имеем  векторов (12),
образующих базис в векторов (12),
образующих базис в 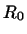 , , 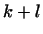 векторов (13), образующих базис в векторов (13), образующих базис в
 , , 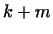 векторов (14), образующих базис в векторов (14), образующих базис в  , и , и
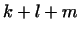 векторов (15), образующих базис в векторов (15), образующих базис в
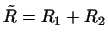 .
Утверждение теоремы обращается, таким образом, в тождество .
Утверждение теоремы обращается, таким образом, в тождество
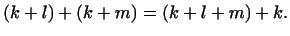
Теорема доказана.
Упражнение
Проверить теорему для случая, когда  и и  -- двумерные
подпространства трехмерного пространства. -- двумерные
подпространства трехмерного пространства.
Из доказанной теоремы следует, например, что двум 15-мерным
подпространствам ``тесно'' в 28-мерном пространстве -- они
пересекаются по крайней мере по двумерному подпространству
(плоскости). Действительно, сумма их размерностей равна 30, а
размерность суммы не может, конечно, превосходить размерности
всего пространства, т.е. 28.
Упражнения
1. Каково наименьшее число измерений пространства, в
котором две плоскости могут пересечься в точке?
2. Доказать, что если
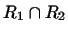 есть нулевое подпространство,
то есть нулевое подпространство,
то
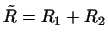 есть прямая сумма есть прямая сумма  и и  , т.е. , т.е.
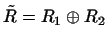 . .
Из результата этого упражнения видно, что теорема 3 этого пункта есть
частный случай теоремы 4.
Упражнение
Показать, что если имеется разложение  в прямую сумму в прямую сумму
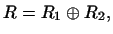 то пересечение
то пересечение  и и  равно нулю и, следовательно, сумма
размерностей этих подпространств равна равно нулю и, следовательно, сумма
размерностей этих подпространств равна  . .
Пусть
 и и
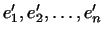 -- два базиса -- два базиса
 -мерного пространства. Пусть, далее, каждый вектор -мерного пространства. Пусть, далее, каждый вектор 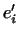 выражается через векторы первого базиса формулами
выражается через векторы первого базиса формулами
Тогда переход от первого базиса ко второму задается матрицей
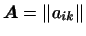 ,
определитель
которой отличен от нуля 2.3. ,
определитель
которой отличен от нуля 2.3.
Обозначим через 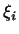 координаты вектора координаты вектора  в первом базисе, а
через в первом базисе, а
через 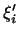 -- его координаты во втором базисе. Найдем, как
выражаются координаты -- его координаты во втором базисе. Найдем, как
выражаются координаты 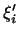 через через 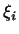 . .
Мы имеем:
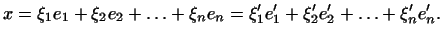 Подставив в это равенство вместо
Подставив в это равенство вместо 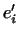 их выражения через их выражения через 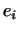 ,
получим: ,
получим:
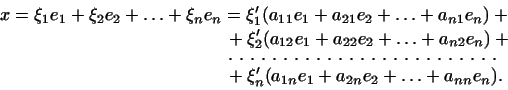 Так как
Так как 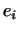 линейно независимы, то коэффициенты при них в правой и
левой частях равенства одинаковы. Получаем: линейно независимы, то коэффициенты при них в правой и
левой частях равенства одинаковы. Получаем:
Сравним формулы (16) и (17). Между ними есть два существенных отличия:
во-первых, поменялись местами штрихованные и нештрихованные буквы и,
во-вторых, в формулах (16) при суммировании меняется первый индекс, а
в формулах (17) второй.
Таким образом, координаты 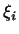 вектора вектора  в первом базисе
выражаются через координаты того же вектора в первом базисе
выражаются через координаты того же вектора  во втором базисе с
помощью матрицы во втором базисе с
помощью матрицы
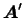 ,
транспонированной к ,
транспонированной к
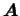 . .
Этот результат можно представить и в другой форме. Решим уравнения
(17) относительно
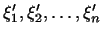 . Получим: . Получим:
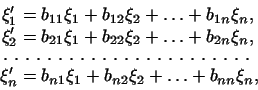 где
где 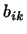 являются элементами матрицы, обратной к матрице являются элементами матрицы, обратной к матрице
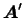 . Таким образом, мы видим, что координаты вектора
преобразуются с помощью матрицы . Таким образом, мы видим, что координаты вектора
преобразуются с помощью матрицы
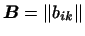 , являющейся
обратной
к , являющейся
обратной
к
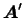 , где , где
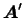 -- матрица, транспонированная к
матрице -- матрица, транспонированная к
матрице
 , задающей преобразование базиса. , задающей преобразование базиса.




Next: 2 евклидово пространство
Up: 1 n-мерное пространство. Линейные
Previous: 1 n-мерное пространство. Линейные
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
|


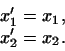
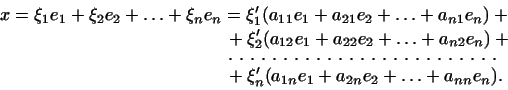 Так как
Так как 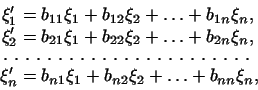 где
где