



Next: 5 приведение квадратичной формы
Up: 1 n-мерное пространство. Линейные
Previous: 3 изоморфизм евклидовых пространств
Subsections
В этом параграфе мы будем опять заниматься аффинным пространством, а
именно, будем изучать простейшие числовые функции от векторов в
аффинном пространстве.
Простейшей функцией в аффинном пространстве является линейная функция.
Определение 4.1
Говорят, что в аффинном пространстве задана
линейная функция (линейная форма),
если каждому вектору  поставлено в соответствие число поставлено в соответствие число  , так
что при этом выполнены условия: , так
что при этом выполнены условия:
1
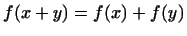 . .
2
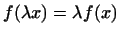 . .
Выберем в  -мерном пространстве произвольный базис -мерном пространстве произвольный базис
 . Так как каждый вектор . Так как каждый вектор  можно представить в виде можно представить в виде
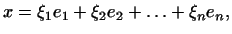 то в силу свойств линейной функции имеем:
то в силу свойств линейной функции имеем:
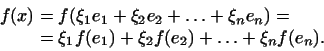 Итак: в
Итак: в  -мерном пространстве с заданным базисом линейная
функция может быть представлена в виде -мерном пространстве с заданным базисом линейная
функция может быть представлена в виде
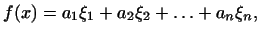 |
(1) |
где
 -- постоянные, зависящие лишь от выбора базиса,
а -- постоянные, зависящие лишь от выбора базиса,
а
 -- координаты вектора в этом
базисе. -- координаты вектора в этом
базисе.
Таким образом, данное выше определение линейной функции совпадает, по
существу, с принятым в алгебре определением линейной функции (линейной
формы); надо лишь иметь в виду, что в нашем случае коэффициенты
зависят от выбора базиса.
Выясним, как меняются коэффициенты линейной функции при замене
одного базиса другим.
Пусть
 и и
 -- два базиса в
-- два базиса в  . Пусть, далее, векторы . Пусть, далее, векторы  выражаются
через базис выражаются
через базис
 формулами формулами
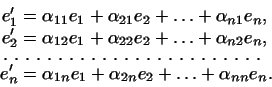 Пусть в базисе
Пусть в базисе
 линейная функция
выражается формулой линейная функция
выражается формулой
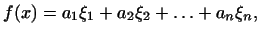 а в базисе
а в базисе
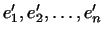 -- формулой -- формулой
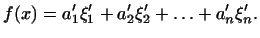 Так как
Так как
 , а , а
 , то , то
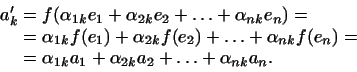 Мы видим, следовательно, что коэффициенты линейной формы
преобразуются при переходе к другому базису так же, как векторы
базиса (или, как иногда говорят, когредиентно векторам
базиса).
Мы видим, следовательно, что коэффициенты линейной формы
преобразуются при переходе к другому базису так же, как векторы
базиса (или, как иногда говорят, когредиентно векторам
базиса).
Пример 1
1. В пространстве, векторами которого являются
непрерывные функции 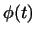 , заданные на отрезке , заданные на отрезке ![$ [a,b]$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img18.gif) ,
рассмотрим функцию ,
рассмотрим функцию 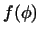 , заданную формулой , заданную формулой
 Эта функция линейна, так как выполняются условия 1
Эта функция линейна, так как выполняются условия 1 и
2 и
2 . .
Действительно, первое из них означает, что интеграл суммы равен
сумме интегралов, а второе означает, что постоянный множитель
можно выносить за знак интеграла.
Пример 2
2. В том же пространстве рассмотрим функцию
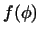 , определенную следующим образом. Выберем на отрезке , определенную следующим образом. Выберем на отрезке
![$ [a,b]$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img18.gif) некоторое значение некоторое значение  и положим и положим
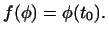 Проверьте, что эта функция
Проверьте, что эта функция 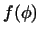 также линейна. также линейна.
Существенную роль в дальнейшем
будут играть билинейные и квадратичные функции (формы).
Определение 4.2
Мы говорим, что 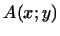 есть
билинейная функция (билинейная форма)
от векторов есть
билинейная функция (билинейная форма)
от векторов  и и  , если: , если:
1 при фиксированном при фиксированном  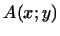 есть линейная функция
от есть линейная функция
от  , ,
2 при фиксированном при фиксированном  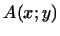 есть линейная функция
от есть линейная функция
от  . .
Иными словами, в силу определения линейной функции условия 1 и
2 и
2 означают соответственно означают соответственно
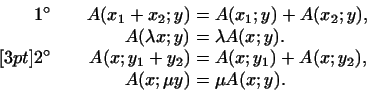
Примеры
1. Рассмотрим  -мерное пространство, в котором
вектор есть совокупность -мерное пространство, в котором
вектор есть совокупность  чисел. Положим чисел. Положим
где  есть вектор есть вектор
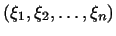 , а , а  -- вектор -- вектор
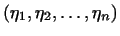 . Формула (2) определяет билинейную
функцию. В самом деле, если зафиксировать . Формула (2) определяет билинейную
функцию. В самом деле, если зафиксировать  , т.е. считать , т.е. считать
 постоянными, то постоянными, то
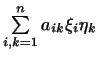 зависит от зависит от 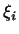 линейно, т.е. есть линейная
функция от линейно, т.е. есть линейная
функция от
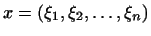 , а при постоянных , а при постоянных
 форма форма 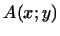 -- линейная функция от -- линейная функция от  . .
2. В пространстве, в котором векторами являются непрерывные
функции 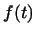 , рассмотрим следующий пример билинейной функции.
Пусть , рассмотрим следующий пример билинейной функции.
Пусть 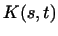 -- некоторая непрерывная функция переменных -- некоторая непрерывная функция переменных 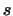 и
и 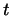 . Положим . Положим
![$\displaystyle A(f; g)=
\HTMLcode[HREF=''\char93 двойной_интеграл'']{A}{\textcolor{green}{\int\limits_a^b\int\limits_a^bK(s,t)f(s)g(t) ds dt.}}
$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img498.gif)
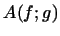 есть билинейная функция векторов есть билинейная функция векторов 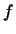 и и 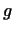 . .
Действительно, условия 1 и 2 и 2 проверяются так же, как и
в примере 1 предыдущего пункта. проверяются так же, как и
в примере 1 предыдущего пункта.
Если
 , то , то
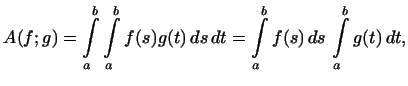 т.е.
т.е. 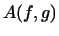 есть произведение линейных функций есть произведение линейных функций
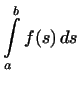 и и
 . .
Упражнение
Показать, что если  и и 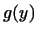 -- линейные
функции, то их произведение -- линейные
функции, то их произведение
 есть билинейная функция. есть билинейная функция.
Определение 4.3
Билинейная функция (форма) называется
симметрической,
если для любых векторов  и и  имеет место равенство имеет место равенство
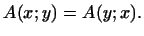
В приведенном выше примере 1 определенная формулой (2) билинейная
форма 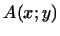 симметрична тогда и только тогда, когда симметрична тогда и только тогда, когда
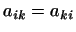 для любых для любых 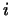 и и  . .
Скалярное произведение 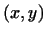 в евклидовом пространстве
является примером симметрической билинейной формы. в евклидовом пространстве
является примером симметрической билинейной формы.
В самом деле, аксиомы 1 , 2 , 2 , 3 , 3 скалярного
произведения ( 2) как раз и означают, что
скалярное произведение есть симметрическая билинейная форма. скалярного
произведения ( 2) как раз и означают, что
скалярное произведение есть симметрическая билинейная форма.
Мы определили билинейную форму аксиоматически. Выберем теперь в
 -мерном пространстве какой-либо базис -мерном пространстве какой-либо базис
 и
выразим билинейную форму и
выразим билинейную форму 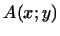 через координаты через координаты
 и и
 векторов векторов  и и  в
этом базисе. Мы имеем: в
этом базисе. Мы имеем:
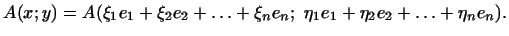 В силу свойств 1
В силу свойств 1 и 2 и 2 билинейной формы билинейной формы
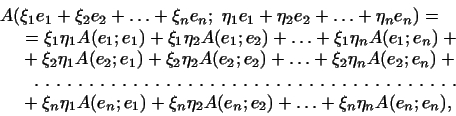 или, короче
или, короче
 Обозначим постоянные
Обозначим постоянные
|

