



Next: 8 комплексное -мерное пространство
Up: 1 n-мерное пространство. Линейные
Previous: 6 приведение к сумме
Subsections
Приводя квадратичную форму  к сумме квадратов, можно по-разному выбирать тот базис, в котором эта
форма приводится к сумме квадратов, т.е. к виду
к сумме квадратов, можно по-разному выбирать тот базис, в котором эта
форма приводится к сумме квадратов, т.е. к виду
 |
(1) |
Все те 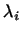 , которые отличны от нуля, можно, заменяя векторы
базиса им пропорциональными, сделать равными , которые отличны от нуля, можно, заменяя векторы
базиса им пропорциональными, сделать равными 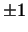 . Таким образом,
канонический вид формы . Таким образом,
канонический вид формы  в некотором соответствующим образом
подобранном базисе вполне можно характеризовать количеством
коэффициентов, равных соответственно нулю, в некотором соответствующим образом
подобранном базисе вполне можно характеризовать количеством
коэффициентов, равных соответственно нулю,  и и  . Так как мы
можем по-разному выбирать тот базис, в котором квадратичная форма
записывается в виде суммы квадратов, то возникает вопрос, зависит ли
количество коэффициентов, равных нулю, . Так как мы
можем по-разному выбирать тот базис, в котором квадратичная форма
записывается в виде суммы квадратов, то возникает вопрос, зависит ли
количество коэффициентов, равных нулю,  и и  , от выбора базиса
или же эти числа зависят лишь от квадратичной формы , от выбора базиса
или же эти числа зависят лишь от квадратичной формы  (являются ее инвариантами).
(являются ее инвариантами).
Например, если квадратичная форма  в некотором базисе в некотором базисе
 имеет матрицу имеет матрицу
 где
где
 и все определители и все определители
![$\displaystyle \arraycolsep3pt
\Delta_1=a_{11}, \Delta_2=
\begin{vmatrix}
a_{11...
...\dots&a_{2n}\\
\hdotsfor[1.5]{4}\\
a_{n1}&a_{n2}&\dots&a_{nn}
\end{vmatrix}$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img745.gif) отличны от нуля, то, как мы показали в
п.2 предыдущего параграфа, все
отличны от нуля, то, как мы показали в
п.2 предыдущего параграфа, все 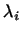 в
формуле (1) отличны от нуля и при приведении в
формуле (1) отличны от нуля и при приведении  к сумме
квадратов по описанному там способу число отрицательных коэффициентов
равно числу перемен знака в ряду определителей к сумме
квадратов по описанному там способу число отрицательных коэффициентов
равно числу перемен знака в ряду определителей
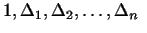 . .
Но мы могли взять другой исходный базис
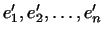 (например, хотя бы взять те же
самые векторы, но в другом порядке); при этом получается другая
матрица (например, хотя бы взять те же
самые векторы, но в другом порядке); при этом получается другая
матрица
 и другие определители и другие определители
 и заранее совершенно неясно, почему число перемен знака в обоих
случаях должно быть одно и то же.
и заранее совершенно неясно, почему число перемен знака в обоих
случаях должно быть одно и то же.
В этом параграфе будет доказана следующая теорема, называемая
законом инерции квадратичной формы:
Теорема 7.1
Если квадратичная форма приведена двумя различными способами
(т.е. в двух различных базисах) к сумме квадратов, то
число положительных коэффициентов, так же как и число отрицательных, в
обоих случаях одно и то же.
Так как общее число коэффициентов 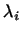 в каноническом виде
квадратичной формы равно в каноническом виде
квадратичной формы равно  , то отсюда непосредственно следует,
что число коэффициентов , то отсюда непосредственно следует,
что число коэффициентов 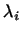 , равных нулю, также есть
инвариант квадратичной формы. , равных нулю, также есть
инвариант квадратичной формы.
Доказательство. Пусть в базисе
 квадратичная форма квадратичная форма
 имеет вид 2.23 имеет вид 2.23
 |
(2) |
при этом
 -- координаты вектора -- координаты вектора
 , т.е. , т.е.
 Пусть в базисе
Пусть в базисе
 эта же квадратичная
форма имеет вид эта же квадратичная
форма имеет вид
 |
(3) |
где
 -- координаты вектора в базисе -- координаты вектора в базисе
 . Нам нужно доказать, что . Нам нужно доказать, что  и и
 . Предположим, что это не так, например, пусть . Предположим, что это не так, например, пусть
 . .
Рассмотрим подпространство  , состоящее из линейных комбинаций
векторов , состоящее из линейных комбинаций
векторов
 . Оно имеет . Оно имеет  измерений.
Подпространство измерений.
Подпространство  , состоящее из линейных комбинаций векторов , состоящее из линейных комбинаций векторов
 , имеет , имеет  измерений. Так
как измерений. Так
как  (ибо мы предположили, что (ибо мы предположили, что  ), то существует
вектор ), то существует
вектор  , лежащий на пересечении , лежащий на пересечении  и и  , т.е. такой,
что , т.е. такой,
что
 и
и
 В базисе
В базисе
 этот вектор имеет координаты этот вектор имеет координаты
 , в базисе , в базисе
 он имеет координаты он имеет координаты
 . Подставляя эти
координаты в формулы (2) и (3), мы получим, с одной стороны, . Подставляя эти
координаты в формулы (2) и (3), мы получим, с одной стороны,
 |
(4) |
(так как не все числа
 равны
нулю), а с другой стороны, равны
нулю), а с другой стороны,
 |
(5) |
2.24.Мы пришли к противоречию, следовательно, неравенство  невозможно. Точно так же доказывается невозможность неравенств
невозможно. Точно так же доказывается невозможность неравенств
 , ,  и и  . Таким образом, закон инерции для
квадратичных форм доказан. . Таким образом, закон инерции для
квадратичных форм доказан.
Определение 7.1
Число отличных от нуля коэффициентов 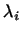 в каноническом виде
квадратичной формы называется
рангом квадратичной формы. в каноническом виде
квадратичной формы называется
рангом квадратичной формы.
Как уже было указано выше, из доказанного нами закона инерции
непосредственно следует, что ранг квадратичной формы зависит только от
самой формы, а не от способа ее приведения к каноническому
виду. Посмотрим, как фактически найти ранг квадратичной формы. Для
этого мы определим ранг квадратичной формы, не прибегая к ее
каноническому виду. Попутно мы получим определение одного
подпространства, тесно связанного с данной билинейной формой.
Определение 7.2
Нулевым подпространством данной билинейной формы 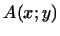 мы называем совокупность
мы называем совокупность 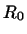 векторов векторов  , удовлетворяющих условию , удовлетворяющих условию
 для любого вектора для любого вектора 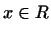 . .
Легко видеть, что 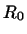 действительно есть подпространство. В самом
деле, пусть действительно есть подпространство. В самом
деле, пусть
 , т.е. , т.е.
 и и
 для
любого для
любого 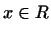 . Тогда . Тогда
 и и
 для
любых для
любых  и и 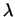 , т.е. , т.е.
 и и
 . .
Поставим вопрос: как найти подпространство 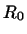 ? Пусть ? Пусть
 -- какой-либо базис в -- какой-либо базис в  . Для того чтобы вектор . Для того чтобы вектор
 |
(6) |
принадлежал нулевому подпространству, достаточно, чтобы
 для для |
(7) |
Действительно, если эти равенства выполнены, то и для любого  имеем имеем
 , так как всякий вектор , так как всякий вектор  есть линейная комбинация
базисных векторов. есть линейная комбинация
базисных векторов.
Подставляя в (7) вместо  его выражение (6), мы приходим к следующей
системе уравнений: его выражение (6), мы приходим к следующей
системе уравнений:
 или, если положить
или, если положить
 , к системе , к системе
 Совокупность векторов
Совокупность векторов  , координаты , координаты
 которых являются решениями этой системы, и образует нулевое
подпространство
которых являются решениями этой системы, и образует нулевое
подпространство 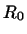 . Как известно из теории линейных уравнений,
размерность этого подпространства равна . Как известно из теории линейных уравнений,
размерность этого подпространства равна  , где , где  --
ранг матрицы --
ранг матрицы
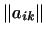 . .
Мы можем теперь сделать следующий вывод:
Ранг матрицы
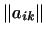 билинейной формы билинейной формы 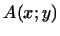 в некотором
базисе не зависит от выбора этого базиса (хотя сама матрица в некотором
базисе не зависит от выбора этого базиса (хотя сама матрица
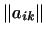 , как мы знаем из 5, зависит
от выбора базиса). , как мы знаем из 5, зависит
от выбора базиса).
В самом деле, ранг этой матрицы равен  , где , где  --
размерность нулевого подпространства. Нулевое же подпространство ни от
какой системы координат вообще не зависит. --
размерность нулевого подпространства. Нулевое же подпространство ни от
какой системы координат вообще не зависит.
Свяжем ранг матрицы квадратичной формы с рангом самой квадратичной
формы. Рангом квадратичной формы мы назвали число отличных от нуля
квадратов в каноническом виде квадратичной формы. Но в каноническом
базисе матрица квадратичной формы имеет вид
![$\displaystyle \begin{pmatrix}
\lambda_1&0&\dots&0\\
0&\lambda_2&\dots&0\\
\noalign{\vskip-2pt}
\hdotsfor[1.5]{4}\\
0&0&\dots&\lambda_n
\end{pmatrix}$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch1img793.gif) и ранг этой матрицы равен
и ранг этой матрицы равен  , где , где  -- число коэффициентов,
отличных от нуля, т.е. равен рангу квадратичной формы. Так как ранг
матрицы квадратичной формы, как мы доказали, не зависит от системы
координат, то и в любой другой системе координат ранг матрицы
квадратичной формы равен рангу самой квадратичной формы 2.25. -- число коэффициентов,
отличных от нуля, т.е. равен рангу квадратичной формы. Так как ранг
матрицы квадратичной формы, как мы доказали, не зависит от системы
координат, то и в любой другой системе координат ранг матрицы
квадратичной формы равен рангу самой квадратичной формы 2.25.
Итак, нами доказана следующая
Теорема 7.2
Матрицы квадратичной формы в различных системах координат имеют один и
тот же ранг  . Этот ранг равен числу квадратов в каноническом виде
формы, коэффициенты при которых отличны от нуля. . Этот ранг равен числу квадратов в каноническом виде
формы, коэффициенты при которых отличны от нуля.
Таким образом, для того чтобы найти ранг квадратичной формы,
нужно вычислить ранг ее матрицы в какой-нибудь одной системе
координат.




Next: 8 комплексное -мерное пространство
Up: 1 n-мерное пространство. Линейные
Previous: 6 приведение к сумме
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
|

