




Next: 13 унитарные преобразования
Previous: 11 линейное преобразование, сопряженное
Subsections
[section] Рассматривается линейное пространство над полем
комплексных числел.
В этом параграфе мы более подробно изучим класс самосопряженных
преобразований  -мерного евклидова пространства. Эти преобразования
часто встречаются в различных приложениях. (Существенную роль
самосопряженные преобразования, правда в бесконечномерном
пространстве, играют в квантовой механике). -мерного евклидова пространства. Эти преобразования
часто встречаются в различных приложениях. (Существенную роль
самосопряженные преобразования, правда в бесконечномерном
пространстве, играют в квантовой механике).
Лемма 12.1
Собственные значения самосопряженного преобразования вещественны.
Доказательство. Пусть 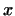 -- собственный вектор самосопряженного преобразования -- собственный вектор самосопряженного преобразования  и и
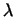 -- соответствующее собственное значение, т.е. -- соответствующее собственное значение, т.е.
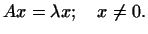 Так как
Так как 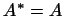 , то , то
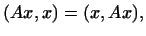 т.е.
т.е.
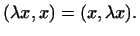 Вынося
Вынося 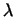 за скобки, получим: за скобки, получим:
 и так как
и так как 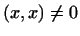 , то , то
 , что и
требовалось доказать. , что и
требовалось доказать.
Лемма 12.2
Пусть  -- самосопряженное линейное преобразование в -- самосопряженное линейное преобразование в  -мерном
пространстве -мерном
пространстве  и и 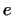 -- его собственный вектор. Совокупность -- его собственный вектор. Совокупность  векторов
векторов 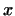 , ортогональных к , ортогональных к 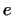 , есть , есть 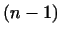 -мерное
подпространство, инвариантное относительно преобразования -мерное
подпространство, инвариантное относительно преобразования  . .
Доказательство. Совокупность  векторов векторов 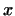 , ортогональных к , ортогональных к 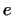 , образует , образует
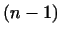 -мерное подпространство. -мерное подпространство.
Покажем, что  инвариантно относительно инвариантно относительно  . Пусть . Пусть
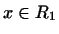 . Это значит, что . Это значит, что 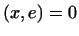 . Тогда и . Тогда и 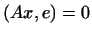 ,
т.е. ,
т.е. 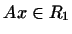 . Действительно, . Действительно,

Мы доказали, что преобразование  не выводит векторы,
принадлежащие не выводит векторы,
принадлежащие  , из , из  , т.е. доказали, что
подпространство , т.е. доказали, что
подпространство  инвариантно относительно инвариантно относительно  . .
Теорема 12.1
Пусть  -- самосопряженное преобразование в -- самосопряженное преобразование в  -мерном евклидовом
пространстве -мерном евклидовом
пространстве  . Тогда существует . Тогда существует  попарно ортогональных
собственных векторов преобразования попарно ортогональных
собственных векторов преобразования  . Соответствующие им
собственные значения вещественны. . Соответствующие им
собственные значения вещественны.
Доказательство. Согласно теореме 1 §10 в  существует хотя бы
один собственный вектор существует хотя бы
один собственный вектор 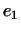 преобразования преобразования  . В силу леммы 2
совокупность векторов, ортогональных к . В силу леммы 2
совокупность векторов, ортогональных к 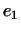 , образует , образует
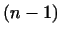 -мерное инвариантное подпространство -мерное инвариантное подпространство  . Будем далее
рассматривать наше преобразование . Будем далее
рассматривать наше преобразование  лишь в лишь в  . В . В  существует собственный вектор
существует собственный вектор 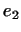 (см. замечание к теореме 1
§10). Совокупность векторов из (см. замечание к теореме 1
§10). Совокупность векторов из  , ортогональных к , ортогональных к 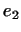 ,
образует ,
образует 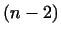 -мерное инвариантное подпространство -мерное инвариантное подпространство 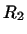 . В нем
существует собственный вектор . В нем
существует собственный вектор 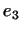 и т.д. и т.д.
Мы получаем, таким образом,  попарно ортогональных собственных
векторов попарно ортогональных собственных
векторов
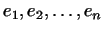 . Согласно лемме 1 соответствующие им
собственные значения вещественны. Теорема доказана. . Согласно лемме 1 соответствующие им
собственные значения вещественны. Теорема доказана.
Так как произведение собственного вектора на любое отличное от
нуля число есть снова собственный вектор, то векторы 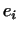 можно
выбрать так, чтобы их длины равнялись единице. можно
выбрать так, чтобы их длины равнялись единице.
Теорема 12.2
Пусть  -- самосопряженное преобразование в -- самосопряженное преобразование в
 -мерном пространстве. Тогда существует ортогональный базис,
в котором матрица преобразования диагональна и вещественна. Верно
также и обратное. -мерном пространстве. Тогда существует ортогональный базис,
в котором матрица преобразования диагональна и вещественна. Верно
также и обратное.
Доказательство. Выберем в качестве базиса построенные в теореме 1 попарно
ортогональные собственные векторы
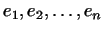 . .
Тогда
 т.е. в этом базисе матрица преобразования
т.е. в этом базисе матрица преобразования  имеет вид имеет вид
![$\displaystyle \begin{pmatrix}\lambda_1&0&\dots&0 0&\lambda_2&\dots&0 \hdotsfor[1.5]{4} 0&0&\dots&\lambda_n \end{pmatrix},$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img431.gif) |
(1) |
где все 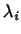 вещественны. вещественны.
Обратно, пусть матрица преобразования  в ортогональном базисе имеет
вид (1). В ортогональном нормированном базисе матрица
сопряженного преобразования в ортогональном базисе имеет
вид (1). В ортогональном нормированном базисе матрица
сопряженного преобразования 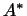 получается из матрицы
преобразования получается из матрицы
преобразования  транспонированием и заменой каждого элемента
комплексно сопряженным (см. §11). Проделав эти операции над
матрицей вида (1) (где все транспонированием и заменой каждого элемента
комплексно сопряженным (см. §11). Проделав эти операции над
матрицей вида (1) (где все 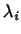 вещественны), мы
получим ту же самую матрицу. Следовательно, преобразованиям вещественны), мы
получим ту же самую матрицу. Следовательно, преобразованиям  и и
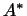 соответствует одна и та же матрица, т.е. соответствует одна и та же матрица, т.е.  . Теорема
полностью доказана. . Теорема
полностью доказана.
Отметим еще следующее свойство собственных векторов самосопряженного
преобразования: собственные векторы, соответствующие различным
собственным значениям, взаимно ортогональны.
Действительно, пусть
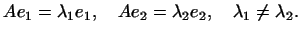 Имеем:
Имеем:
 т.е.
т.е.
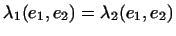 или
или
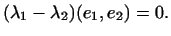 Так как
Так как
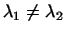 , то , то
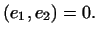
Замечание
Из доказанной теоремы следует, что наглядно-геометрический смысл
произвольного самосопряженного преобразования таков; в пространстве
выделяется  попарно ортогональных направлений (собственных
направлений). Каждому из этих направлений ставится в соответствие
действительное число (собственное значение). По каждому из этих
направлений производится растяжение (сжатие) пространства в попарно ортогональных направлений (собственных
направлений). Каждому из этих направлений ставится в соответствие
действительное число (собственное значение). По каждому из этих
направлений производится растяжение (сжатие) пространства в
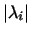 раз и, кроме того, зеркальное отражение в плоскости,
ортогональной к данному направлению, если соответствующее раз и, кроме того, зеркальное отражение в плоскости,
ортогональной к данному направлению, если соответствующее 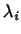 отрицательно.
отрицательно.
Параллельно с понятием самосопряженного преобразования вводится
понятие эрмитовой матрицы.
Матрица
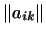 называется
эрмитовой,
если называется
эрмитовой,
если
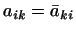 . .
Ясно, что для того чтобы преобразование  было самосопряженным,
необходимо и достаточно, чтобы его матрица в каком-нибудь
ортогональном базисе была эрмитовой. было самосопряженным,
необходимо и достаточно, чтобы его матрица в каком-нибудь
ортогональном базисе была эрмитовой.
Упражнение
Возвести матрицу
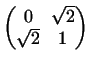 в 28-ю степень.
в 28-ю степень.
Указание. Привести эту матрицу к диагональной форме, затем
возвести ее в указанную степень и, наконец, вернуться к прежнему
базису.
Применим полученные в п.1 результаты к квадратичным формам.
Мы знаем, что всякой эрмитовой билинейной форме соответствует
самосопряженное линейное преобразование. Из теоремы 2 этого
параграфа вытекает важная
Теорема 12.3
Пусть  -- евклидово -- евклидово  -мерное пространство и
пусть -мерное пространство и
пусть 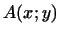 -- эрмитова билинейная форма в -- эрмитова билинейная форма в  . Тогда в . Тогда в  существует ортогональный нормированный базис, в котором
соответствующая
существует ортогональный нормированный базис, в котором
соответствующая 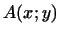 квадратичная форма записывается в виде
суммы квадратов: квадратичная форма записывается в виде
суммы квадратов:
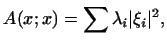 где
где 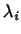 вещественны, а вещественны, а  -- координаты
вектора -- координаты
вектора 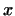 3.7. 3.7.
Доказательство. Если 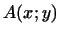 -- эрмитова билинейная форма, т.е. -- эрмитова билинейная форма, т.е.
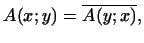 то (см. §11) существует такое самосопряженное линейное
преобразование
то (см. §11) существует такое самосопряженное линейное
преобразование  , что , что
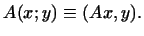 Выберем в
Выберем в  в качестве векторов ортогонального нормированного базиса
систему попарно ортогональных собственных векторов самосопряженного
преобразования в качестве векторов ортогонального нормированного базиса
систему попарно ортогональных собственных векторов самосопряженного
преобразования  (это возможно в силу теоремы 1). Тогда (это возможно в силу теоремы 1). Тогда
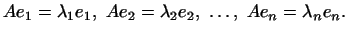 Пусть
Пусть
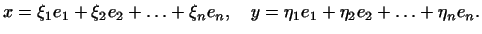 Так как
Так как
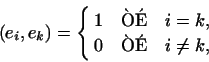 то
то
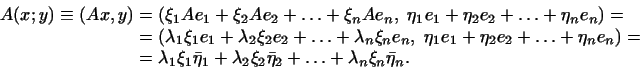 В частности,
В частности,
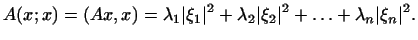 Теорема доказана.
Теорема доказана.
Нахождение в евклидовом пространстве ортогонального нормированного
базиса, в котором данная квадратичная форма приводится к сумме
квадратов, называется приведением этой формы к главным осям.
Теорема 12.4
Пусть  -- аффинное -- аффинное  -мерное пространство и -мерное пространство и
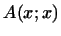 и и 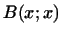 -- две эрмитовы квадратичные формы,
причем форма -- две эрмитовы квадратичные формы,
причем форма 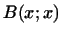 -- положительно определенная. Тогда
существует базис, в котором обе эти формы записываются в виде
суммы квадратов. -- положительно определенная. Тогда
существует базис, в котором обе эти формы записываются в виде
суммы квадратов.
Доказательство. Введем в  скалярное произведение, положив скалярное произведение, положив
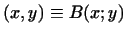 ,
где ,
где  -- отвечающая -- отвечающая 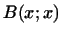 билинейная форма. Это является
законным, так как аксиомы скалярного произведения означают, что билинейная форма. Это является
законным, так как аксиомы скалярного произведения означают, что
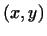 есть эрмитова билинейная форма, соответствующая положительно
определенной квадратичной форме (§8). Пространство есть эрмитова билинейная форма, соответствующая положительно
определенной квадратичной форме (§8). Пространство  станет,
таким образом, евклидовым. Согласно теореме 3 в станет,
таким образом, евклидовым. Согласно теореме 3 в  существует
ортогональный 3.8 нормированный базис существует
ортогональный 3.8 нормированный базис
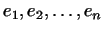 , в котором форма , в котором форма 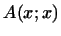 приводится к сумме квадратов, т.е. к
виду приводится к сумме квадратов, т.е. к
виду
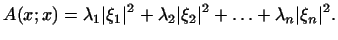 |
(2) |
В нормированном ортогональном базисе скалярное произведение имеет
вид
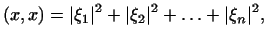 т.е.
т.е.
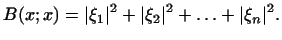 |
(3) |
Мы нашли, таким образом, базис, в котором обе квадратичные формы
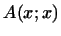 и и 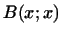 одновременно приводятся к сумме квадратов,
что и требовалось. одновременно приводятся к сумме квадратов,
что и требовалось.
В теореме 4 показано, что в  существует базис, в котором эрмитовы
квадратичные формы существует базис, в котором эрмитовы
квадратичные формы  и и 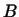 имеют вид (2) и (3).
Покажем, как найти числа имеют вид (2) и (3).
Покажем, как найти числа
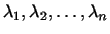 . .
В каноническом виде матрицы квадратичных форм  и и 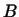 имеют вид имеют вид
![$\displaystyle \arraycolsep3pt
\boldsymbol{A}=
\begin{pmatrix}
\lambda_1&0&\dots...
...&0&\dots&0\\
0&1&\dots&0\\
\hdotsfor[1.5]{4}\\
0&0&\dots&1
\end{pmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img459.gif) Следовательно,
Следовательно,
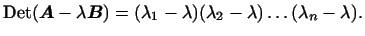 |
(4) |
При переходе к другому базису матрицы эрмитовых квадратичных форм  и
и 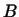 переходят в переходят в
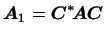 и
и
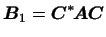 . Поэтому, если . Поэтому, если
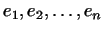 -- произвольный базис, то в этом базисе -- произвольный базис, то в этом базисе
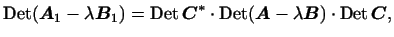 т.е. отличается лишь постоянным множителем от выражения (4).
Отсюда следует, что числа
т.е. отличается лишь постоянным множителем от выражения (4).
Отсюда следует, что числа
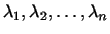 являются корнями следующего уравнения:
являются корнями следующего уравнения:
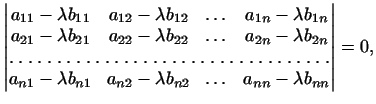 где
где
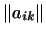 и и
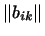 -- матрицы форм -- матрицы форм 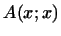 и и
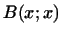 в каком-нибудь базисе в каком-нибудь базисе
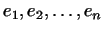 . .
Замечание
Требование положительной определенности одной из форм является
существенным, о чем свидетельствует следующий пример: две квадратичные
формы
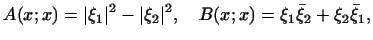 из которых ни одна не является положительно определенной, не могут
быть одновременно приведены к сумме квадратов. В самом деле, первой
форме соответствует матрица
из которых ни одна не является положительно определенной, не могут
быть одновременно приведены к сумме квадратов. В самом деле, первой
форме соответствует матрица
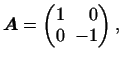 а второй -- матрица
а второй -- матрица
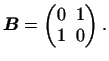 Рассмотрим матрицу
Рассмотрим матрицу
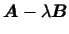 , где , где
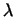 -- вещественный параметр. Ее детерминант равен -- вещественный параметр. Ее детерминант равен
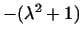 . Так как он не имеет вещественных корней, то,
согласно сказанному выше, обе формы не могут быть приведены
одновременно к сумме квадратов. . Так как он не имеет вещественных корней, то,
согласно сказанному выше, обе формы не могут быть приведены
одновременно к сумме квадратов.





Next: 13 унитарные преобразования
Previous: 11 линейное преобразование, сопряженное
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
| 

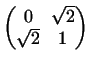 в 28-ю степень.
в 28-ю степень.
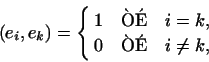 то
то
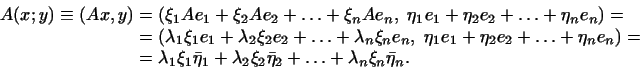 В частности,
В частности,
![$\displaystyle \arraycolsep3pt
\boldsymbol{A}=
\begin{pmatrix}
\lambda_1&0&\dots...
...&0&\dots&0\\
0&1&\dots&0\\
\hdotsfor[1.5]{4}\\
0&0&\dots&1
\end{pmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img459.gif) Следовательно,
Следовательно,
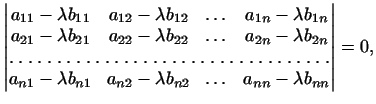 где
где
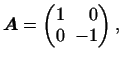 а второй -- матрица
а второй -- матрица
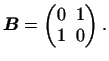 Рассмотрим матрицу
Рассмотрим матрицу