




Next: 14 перестановочные линейные преобразования
Previous: 12 самосопряженные (эрмитовы) преобразования
[section] Рассматривается
линейное пространство над полем комплексных числел.
Мы определили в §11 унитарные преобразования равенством
 |
(1) |
Это определение имеет простой геометрический смысл. А именно:
Всякое унитарное преобразование U в евклидовом  -мерном
пространстве -мерном
пространстве  сохраняет скалярное произведение, т.е. сохраняет скалярное произведение, т.е.
 для всех
для всех  . Обратно, всякое линейное преобразование . Обратно, всякое линейное преобразование
 , сохраняющее скалярное произведение, унитарно [т.е.
удовлетворяет условию (1)]. , сохраняющее скалярное произведение, унитарно [т.е.
удовлетворяет условию (1)].
В самом деле, если дано, что  , то , то

Обратно, если для любых векторов 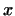 и и 
 то
то
 т.е.
т.е.

Так как из равенства билинейных форм следует равенство
соответствующих преобразований, то  , т.е. , т.е.  унитарно. унитарно.
В частности, при  имеем: имеем:
 т.е. унитарное преобразование
т.е. унитарное преобразование  не меняет длин векторов. не меняет длин векторов.
Упражнение
Доказать, что если линейное преобразование сохраняет
длины всех векторов, то оно унитарно.
Запишем условия унитарности линейного преобразования в матричной
форме. Для этого выберем какой-либо ортогональный нормированный базис
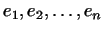 . Пусть в этом базисе
преобразованию . Пусть в этом базисе
преобразованию  соответствует матрица соответствует матрица
![$\displaystyle \arraycolsep3pt \begin{pmatrix}a_{11}&a_{12}&\dots&a_{1n} a_{2...
...&\dots&a_{2n} \hdotsfor[1.5]{4} a_{n1}&a_{n2}&\dots&a_{nn} \end{pmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img479.gif) |
(2) |
Тогда сопряженному преобразованию  соответствует матрица соответствует матрица
![$\displaystyle \arraycolsep3pt \begin{pmatrix}\bar a_{11}&\bar a_{21}&\dots&\bar...
... \hdotsfor[1.5]{4} \bar a_{1n}&\bar a_{2n}&\dots&\bar a_{nn} \end{pmatrix}.$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img481.gif) |
(3) |
Условие унитарности  означает, что произведение матриц
(2) и (3) есть единичная матрица. Если перемножить
их и приравнять элементы произведения соответственным элементам
единичной матрицы, то получим: означает, что произведение матриц
(2) и (3) есть единичная матрица. Если перемножить
их и приравнять элементы произведения соответственным элементам
единичной матрицы, то получим:
 |
(4) |
Итак, в ортогональном нормированном базисе условие  означает, что сумма произведений элементов какой-либо строки матрицы
преобразования
означает, что сумма произведений элементов какой-либо строки матрицы
преобразования  на элементы, сопряженные к элементам другой строки,
равна нулю, а сумма квадратов модулей элементов любой строки равна
единице. на элементы, сопряженные к элементам другой строки,
равна нулю, а сумма квадратов модулей элементов любой строки равна
единице.
Так как  также есть условие унитарности, то мы имеем
также: также есть условие унитарности, то мы имеем
также:
 |
(5) |
Это условие аналогично предыдущему, но вместо строк в нем
участвуют столбцы матрицы.
Условие (5) имеет простой геометрический смысл. Действительно,
скалярное произведение векторов
 и
и
 равно
равно
 (так как (так как
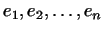 -- это ортогональный нормированный
базис); поэтому -- это ортогональный нормированный
базис); поэтому
Следовательно, для того чтобы линейное преобразование было
унитарным, необходимо и достаточно, чтобы оно переводило какой-либо
ортогональный нормированный базис
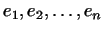 снова в
ортогональный и нормированный базис снова в
ортогональный и нормированный базис
 . .
Матрица
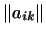 , элементы которой удовлетворяют
условиям (4), либо, что то же самое, условиям (5),
называется унитарной матрицей. Унитарные матрицы являются, как
мы видели, матрицами унитарных преобразований в ортогональном
нормированном базисе. Так как переход от одного ортогонального
нормированного к другому задается унитарным преобразованием, то
матрица перехода от одного ортогонального нормированного базиса к
другому такому же является унитарной. , элементы которой удовлетворяют
условиям (4), либо, что то же самое, условиям (5),
называется унитарной матрицей. Унитарные матрицы являются, как
мы видели, матрицами унитарных преобразований в ортогональном
нормированном базисе. Так как переход от одного ортогонального
нормированного к другому задается унитарным преобразованием, то
матрица перехода от одного ортогонального нормированного базиса к
другому такому же является унитарной.
Посмотрим, к какому простейшему виду можно привести матрицу унитарного
преобразования при соответствующем выборе базиса.
Лемма 13.1
Собственные значения унитарного преобразования по модулю равны  . .
Доказательство. Пусть 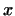 -- собственный вектор унитарного преобразования -- собственный вектор унитарного преобразования  и и
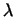 -- соответствующее собственное значение, т.е. -- соответствующее собственное значение, т.е.
 Тогда
Тогда
 т.е.
т.е.
 , значит , значит
 , что и
требовалось доказать. , что и
требовалось доказать.
Лемма 13.2
Пусть  -- унитарное линейное преобразование в -- унитарное линейное преобразование в  -мерном
пространстве -мерном
пространстве  и и 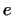 -- его собственный вектор, т.е. -- его собственный вектор, т.е.
 Тогда
Тогда 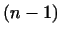 -мерное подпространство -мерное подпространство  , состоящее из векторов , состоящее из векторов 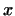 ,
ортогональных к ,
ортогональных к 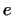 , инвариантно относительно , инвариантно относительно  . .
Доказательство. Пусть 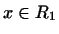 , т.е. , т.е. 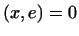 . Покажем, что . Покажем, что  , т.е. что , т.е. что
 . В самом деле, . В самом деле,
 А так как
А так как
 , то , то
 . Но в силу леммы 1 . Но в силу леммы 1
 , поэтому , поэтому  , т.е. , т.е.  . Следовательно,
подпространство . Следовательно,
подпространство  инвариантно относительно инвариантно относительно  . .
Теорема 13.1
Пусть  -- унитарное преобразование в -- унитарное преобразование в  -мерном евклидовом
пространстве. Тогда существует -мерном евклидовом
пространстве. Тогда существует  попарно ортогональных
собственных векторов преобразования попарно ортогональных
собственных векторов преобразования  . Соответствующие им
собственные значения по модулю равны единице. . Соответствующие им
собственные значения по модулю равны единице.
Доказательство. В силу теоремы 1 §10 преобразование  , как и всякое линейное
преобразование, имеет в , как и всякое линейное
преобразование, имеет в  хотя бы один собственный вектор.
Обозначим его хотя бы один собственный вектор.
Обозначим его 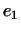 . Согласно лемме 2, . Согласно лемме 2, 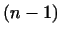 -мерное подпространство -мерное подпространство
 , состоящее из всех векторов пространства , состоящее из всех векторов пространства  , ортогональных к , ортогональных к
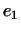 , инвариантно относительно , инвариантно относительно  . Следовательно, в . Следовательно, в  имеется
хотя бы один собственный вектор имеется
хотя бы один собственный вектор 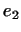 преобразования преобразования  . Через . Через 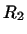 обозначим инвариантное подпространство, состоящее из всех векторов,
принадлежащих
обозначим инвариантное подпространство, состоящее из всех векторов,
принадлежащих  и ортогональных к и ортогональных к 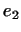 . В . В 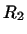 содержится
некоторый собственный вектор содержится
некоторый собственный вектор 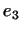 преобразования преобразования  и т.д.;
продолжая этот процесс, мы построим и т.д.;
продолжая этот процесс, мы построим  попарно ортогональных
собственных векторов попарно ортогональных
собственных векторов
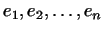 преобразования преобразования  .
Согласно лемме 1 собственные значения, соответствующие собственным
векторам .
Согласно лемме 1 собственные значения, соответствующие собственным
векторам
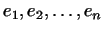 , по модулю равны , по модулю равны  . .
Теорема 13.2
Для каждого унитарного преобразования  в в
 -мерном пространстве -мерном пространстве  существует нормированный
ортогональный базис, в котором матрица преобразования существует нормированный
ортогональный базис, в котором матрица преобразования  диагональна, т.е. имеет вид:
диагональна, т.е. имеет вид:
![$\displaystyle \begin{pmatrix}\lambda_1&0&\dots&0 0&\lambda_2&\dots&0 \hdotsfor[1.5]{4} 0&0&\dots&\lambda_n \end{pmatrix},$](http://images.nature.web.ru/nature/2000/10/02/0001151602/ch2img431.gif) |
(7) |
причем
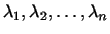 -- числа, по модулю
равные единице. -- числа, по модулю
равные единице.
Доказательство. Пусть  -- унитарное преобразование. Тогда -- унитарное преобразование. Тогда
 попарно ортогональных нормированных собственных векторов,
построенных в предыдущей теореме, образуют искомый базис.
Действительно, попарно ортогональных нормированных собственных векторов,
построенных в предыдущей теореме, образуют искомый базис.
Действительно,
 и, следовательно, матрица преобразования
и, следовательно, матрица преобразования  в базисе в базисе
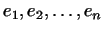 имеет вид (7). Числа имеет вид (7). Числа
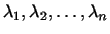 по модулю равны по модулю равны  в силу леммы 1. Теорема
доказана. в силу леммы 1. Теорема
доказана.
Упражнения
1. Доказать, что верно и обратное, т.е. если в
некотором ортогональном базисе матрица преобразования  имеет
вид (7), то имеет
вид (7), то  унитарно. унитарно.
2. Доказать, что если  -- самосопряженное преобразование, то
преобразование -- самосопряженное преобразование, то
преобразование
 существует и является унитарным. существует и является унитарным.
3. Пусть  -- унитарное преобразование. Доказать, что если
преобразование -- унитарное преобразование. Доказать, что если
преобразование  обратимо, то преобразование обратимо, то преобразование
 самосопряженное.
самосопряженное.
Так как матрица перехода от одного ортогонального нормированного
базиса к другому задается унитарной матрицей, то полученный в этом
параграфе результат мы можем в матричных терминах сформулировать
следующим образом:
Пусть
 -- заданная унитарная матрица. Тогда существует
такая унитарная матрица -- заданная унитарная матрица. Тогда существует
такая унитарная матрица
 , что , что
 представима в
виде представима в
виде
 где
где
 -- диагональная матрица, у которой по диагонали
стоят числа, по модулю равные -- диагональная матрица, у которой по диагонали
стоят числа, по модулю равные  . .
Аналогично, основной результат в п.1 §12 в матричных терминах
формулируется так:
Пусть
 -- заданная эрмитова матрица. Тогда -- заданная эрмитова матрица. Тогда
 может быть представлена в виде может быть представлена в виде
 где
где
 -- унитарная матрица, а -- унитарная матрица, а
 --
диагональная матрица, у которой по диагонали стоят вещественные числа. --
диагональная матрица, у которой по диагонали стоят вещественные числа.





Next: 14 перестановочные линейные преобразования
Previous: 12 самосопряженные (эрмитовы) преобразования
Vadim Yu. Radionov
2000-08-30
Посмотреть комментарии[2]
|

