Научная Сеть >> Интерференция света

Наука >> Физика >> Общая физика >> Оптика | Обзорные статьи

Написать комментарий

Добавить новое сообщение

См. также

4 января - день рождения Исаака Ньютона

Когерентный и некогерентный свет: Как измерить время когерентности

Лабиринты фотонных кристаллов: сверхрешетка

Огонь, вода и ... мыльные нитки

Кольца Ньютона

Эффекты Джозефсона в сверхпроводниках: Сверхпроводниковые квантовые интерферометры

Корпускулярно-волновой интерферометр для макромолекул

Когерентный и некогерентный свет: Практическое значение когерентности света

Десять наиболее красивых физических экспериментов

Магматизм Земли: поляризационный микроскоп

Принципы голографии: Динамическая голография

Новые магматические горные породы.: шлиф

Динамическая голография и проблема обращения волнового фронта: Использование нелинейных сред для ОВФ

Принципы голографии: Введение

Фундаментальные взаимодействия: Гравитационное взаимодействие

Антенна: внешняя задача теории антенн

Интерференция света

Научно-образовательный сервер "Оптика",
ИТМО, Санкт-Петербург.

Содержание

В тех случаях, когда интерференционные лучи выходят из какой либо точки протяженного источника симметрично относительно перпендикуляра к линии S'S'', проведенного из этой точки (т.е. когда протяженный источник S'S'' ориентирован перпендикулярно оси симметрии установки), угол $\beta_2=\pi-\beta_1$ и $cos{\beta_2}=- cos{\beta_1}$ . Тогда можно записать $D sin \omega \approx \lambda/4$ , где $2\omega$ - апертура интерференции.
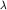При больших апертурах наблюдать интерференцию можно только от источников, размеры которых меньше длины световой волны. Если $\omega \gg \pi/2$ , т.е. интерферирующие лучи выходят из источника почти в противоположных направлениях, то следует, что его протяженность D должна быть меньше $\lambda$ /4. Для наблюдения интерференции с использованием источника, размеры которого много меньше длины волны света, геометрия эксперимента должна быть такой, чтобы интерферирующие лучи выходили из источника под малым углом друг к другу. Когда $\beta_2 \gg \beta_1 \equiv \beta$ , приближенно можно написать $cos{\beta_1}-cos{\beta_2} \gg sin \beta (\beta_2-\beta_1)=2 \omega sin \beta$ и критерий принимает вид $D sin \beta \cdot 2 \omega \approx \lambda/2$ , т.е. $D_{\perp} \omega \approx \lambda/4$ - при малых апертурах интерференции ( $\omega \ll 1$ ) играет роль протяженность источника только в направлении, перпендикулярном направлению выходящих из него лучей: $D_{\perp}=D sin \beta$ . Применим данный критерий к рассмотренным выше интерференционным опытам:

опыту Юнга;

зеркалам Френеля;

бипризме Френеля;

опыту Поля.

Зависимость видности полос от апертуры интерференции можно наглядно продемонстрировать в опыте с зеркалом Ллойда.

Опыт Юнга

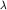В опыте Юнга $2 \omega \gg d/L$ , поэтому ширина дополнительной щели S и ее угловой размер $\vartheta =D_{\perp} /L$ должны удовлетворять условию $D_{\perp} \approx \lambda L/(2d)$ , $\vartheta \approx \lambda /(2d)$ . При $\lambda$ =5 $\cdot$ 10^-5 см, L=1 м и d=0,5 мм находим,что ширина щели $D_{\perp}$ должна быть меньше 0,5 мм.

Зеркала Френеля

Рассмотрим опыт с зеркалами Френеля. Для точки наблюдения P, лежащей в центре интерференционного поля, угол $2\omega$ между выходящими из источника S интерферирующими лучами легко найти. Угол $\delta$ (равный углу между зеркалами) является внешним для треугольника S₁OP и поэтому $\delta =\omega +\alpha /2$ . Для половины угла схождения лучей можно написать $\alpha /2=a\delta /(a+b)$ . Исключая из этих уравнений $\alpha /2$ , находим $\omega =\delta b/(a+b)$ . Подставляя $\omega$ , получаем следующее ограничение на ширину $D_{\perp}$ щели источника S: $D_{\perp} \approx \lambda (a+b)/(4b\delta)$ . Если $b \gg a$ , то это условие принимает вид $D_{\perp} \approx \lambda /(4\delta)$ . Чтобы можно было наблюдать полосы с источником, для которого $D_{\perp} \gg \lambda$ , угол между зеркалами должен быть очень мал ( $\delta \ll 1$ ). Можно показать, что в опыте с зеркалами Френеля апертура интерференции $2\omega$ имеет практически одно и то же значение при любом положении точки наблюдения P на экране в области, где перекрываются интерферирующие пучки. Поэтому видность полос одинакова по всему интерференционному полю.

Бипризма Френеля

В опыте с бипризмой Френеля апертура интерференции также практически одинакова по всему полю и равна $2\omega =\beta (n-1)b/(a+b) \gg \beta(n-1)$ (последнее справедливо при $a \ll b$ ).
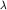Подставляя $\omega$ , находим $D_{\perp} \approx \lambda /[2\beta (n-1)]$ . При использовании протяженного источника с $D_{\perp} \gg \lambda$ угол $\beta$ бипризмы должен быть мал.

Опыт Поля

При анализе интерференционного опыта Поля для упрощения будем пренебрегать преломлением в слюде, т.е. заменим пластинку двумя отражающими параллельными плоскостями, расстояние между которыми равно толщине h пластинки. Тогда расстояние между вторичными источниками S₁ и S₂ (мнимыми изображениями источника S) равно 2h. Легко видеть, что угол схождения лучей в точку наблюдения в этом опыте равен апертуре интерференции 2\omega. Расстояние |S₁P| равно $(a+b)/cos\vartheta$ , поэтому $2\omega =2h sin \vartheta /|S_1 P|=h sin {2\vartheta} /(a+b)$ . Толщина h листочка слюды очень мала ( $\gg$ 0,05 мм) по сравнению с a+b ( $\gg$ 5 м), поэтому мала и апертура интерференции $2\omega$ (при любом положении точки наблюдения P, включая $\vartheta =45^{\circ}$ ). Следовательно, размер источника S может быть достаточно большим: находим $D_{\perp} \approx \lambda (a+b)/(2 h sin {2\vartheta} )$ . При $\lambda$ = 5 $\cdot$ 10^-5 см, h=0,05 мм, a+b=5 м и $\vartheta =45^{\circ}$ должно быть $D_{\perp} \approx$ 2,5 см. Для демонстрации опыта Поля можно использовать небольшую ртутную лампу без всяких дополнительных щелей, что обеспечивает большую светосилу. С помощью листочка слюды площадью несколько квадратных сантиметров можно получить яркую интерференционную картину больших размеров, покрывающую потолок и стены аудитории. Размер источника ( $\gg$ 10 мм) гораздо больше расстояния |S₁S₂|( $\gg$ 0,1 м), так что мнимые изображения источника почти полностью перекрываются. При наблюдении локализованных в бесконечности полос равного наклона оба интерферирующих луча выходят из источника в одном направлении, т.е. апертура интерференции равна нулю. Поэтому здесь нет никаких ограничений на размер источника.

Назад | Вперед