Оператор момента импульса частицы определим, используя принцип соответствия, в виде
Напомним (см. п. 5), что оператор момента естественно определяется как генератор группы вращений в пространстве волновых функций.
На основе коммутаторов (фундаментальных квантовых скобок Пуассона) ![$[\hat x_k, \hat p_n]=i\hbar\delta_{kn}$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula79.gif) получаем получаем
Используя циклическую перестановку индексов, получим еще два соотношения. В итоге:
В тензорной форме:
или символически:
Введем оператор квадрата момента
Вычислим его коммутатор с компонентами момента:
Итак, квадрат момента коммутирует со всеми компонентами:
Этого и следовало ожидать, так как скаляр при поворотах системы координат не изменяется.
Рассмотрим теперь алгебру операторов момента в общем виде, не фиксируя ее представление. Выбирая 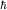 в качестве естественной единицы измерения момента и обозначая (безразмерные) компоненты в качестве естественной единицы измерения момента и обозначая (безразмерные) компоненты 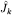 , получаем коммутационные соотношения в виде: , получаем коммутационные соотношения в виде:
Введем неэрмитовы сопряженные друг другу операторы
Тогда получим коммутаторы:
Квадрат момента удобно записать так:
Отсюда с учетом 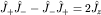 находим находим
В силу ![$[{\bf\hat J}^2,\hat J_z]=0$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula95.gif) существует общая система собственных векторов этих операторов: существует общая система собственных векторов этих операторов:
Покажем, что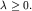 Имеем Имеем
где учтена эрмитовость операторов 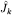 . .
Из полученных выше тождеств для произведений операторов 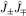 находим: находим:
Умножив слева скалярно на 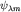 обе части этих равенств, получим с учетом обе части этих равенств, получим с учетом 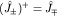 : :
Следовательно,
В силу неотрицательности нормы вектора имеем:
или
Отсюда
где
Получаем решение системы неравенств:
Обозначим
Тогда находим:
Далее собственные векторы будем обозначать 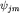 .
Так как .
Так как 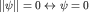 , то , то 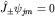 тогда и только тогда, когда тогда и только тогда, когда 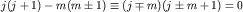 .
С учетом ограничения .
С учетом ограничения 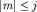 приходим к выводу: приходим к выводу:
Пусть 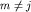 . Учитывая соотношения . Учитывая соотношения
находим
Следовательно,
Аналогично найдем:
Выше было получено:
Рассмотрим последовательность векторов
Очевидно, что
,
причем
Ясно, что существует целое неотрицательное число n+ такое, что
т.е. m+n+=j.
Итак,
причем существует n+ собственных векторов операторов 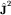 и и 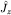 : :
отвечающих собственным значениям оператора 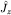 , равным , равным
Аналогично получаем для 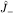 последовательность векторов последовательность векторов
принадлежащих СЗ 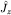 , равным соответственно , равным соответственно
Из условий
следует, что
Итак, СЗ оператора 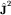 равны j(j+1), где равны j(j+1), где
СЗ оператора 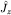 таковы: таковы:
Для общего СВ 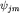 операторов операторов 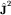 и и 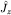 возможны 2j+1 значений m: возможны 2j+1 значений m:
Вернемся к соотношениям
Выберем 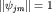 и фиксируем фазу вектора и фиксируем фазу вектора 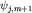 так, чтобы так, чтобы 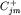 было действительным неотрицательным числом. Тогда получим было действительным неотрицательным числом. Тогда получим
Отсюда с учетом уже полученного соотношения
находим:
Подведем итоги. Исходя из существования одного вектора 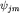 , мы построили всего 2j+1 ортонормированных векторов: , мы построили всего 2j+1 ортонормированных векторов:
Они образуют базис 2j+1-мерного пространства H(j) , инвариантного относительно действия операторов момента 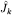 .
Соберем вместе основные полученные соотношения: .
Соберем вместе основные полученные соотношения:
Исследование свойств момента было основано только на коммутационных соотношениях и эрмитовости операторов момента, а также на неотрицательности нормы векторов состояний. Далее мы рассмотрим конкретные представления алгебры момента.
Назад | Вперед
Посмотреть комментарии[1]
|

