Оператор орбитального момента частицы определен выше:
В координатном представлении получаем:
Найдем выражения для компонент момента в сферических координатах, связанных с декартовыми координатами соотношениями:
Вычисляем производные волновой функции  как сложной функции сферических координат: как сложной функции сферических координат:
где  .
Умножим первое равенство на .
Умножим первое равенство на  , а второе на , а второе на  и сложим почленно. Получим соответственно: и сложим почленно. Получим соответственно:
В результате находим искомые выражения:
Кроме того,
Используя известное выражение для квадрата момента (см. выше)
нетрудно отсюда получить для него представление в сферических координатах:
где  - угловая часть оператора Лапласа. - угловая часть оператора Лапласа.
Найдем общие собственные функции операторов  : :
Решаем второе уравнение:
Потребуем однозначности функции:
Тогда  , и собственные значения , и собственные значения
Замечание. Требование однозначности волновой функции слишком жесткое (достаточно однозначности модуля функции), и его можно снять (см. ниже).
Из общей теории (см. выше) известно, что  . Поэтому для орбитального момента имеем только целые значения . Поэтому для орбитального момента имеем только целые значения
Рассмотрим собственную функцию при  : :
Она удовлетворяет уравнению
или
Для функции  после замены переменной после замены переменной  получаем уравнение, которое легко решается: получаем уравнение, которое легко решается:
Итак, для каждого целого и и  существует единственная собственная функция существует единственная собственная функция
Следовательно, общий спектр операторов  в целом невырожден: каждой паре собственных значений в целом невырожден: каждой паре собственных значений  отвечает одна собственная функция. отвечает одна собственная функция.
Нормируем  на единицу и фиксируем фазу. Тогда получим ортонормированную систему функций на единицу и фиксируем фазу. Тогда получим ортонормированную систему функций  : :
Условие полноты системы:
Далее требуем выполнения условий (см. выше):
Тем самым определены относительные фазы 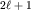 функций, отвечающих заданному функций, отвечающих заданному  . Фиксируем фазу одной из функций. Мы выберем . Фиксируем фазу одной из функций. Мы выберем  так, чтобы так, чтобы  было действительным положительным числом. было действительным положительным числом.
Произвольную функцию  получаем из получаем из многократным действием операторов многократным действием операторов  : :
Далее используем явный вид  : :
Отсюда
Имеем функцию (см. выше)
Нормируя ее условием  , получим , получим
Теперь находим
При  отсюда следует отсюда следует
Тогда находим эквивалентное выражение для собственных функций:
В частности, при m=0 получаем:
Введем полиномы Лежандра
Отсюда и из введенного выше условия фиксации фазы функции  находим нормировочный коэффициент находим нормировочный коэффициент
Определим функции Лежандра в виде:
где  .
Тогда окончательно получим: .
Тогда окончательно получим:
Отсюда находим соотношение между функциями  : :
В математической литературе  называются сферическими функциями. называются сферическими функциями.
Рассмотрим их преобразование при дискретном преобразовании координат - пространственной инверсии 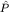 , отвечающей переходу от правой системы координат к левой: , отвечающей переходу от правой системы координат к левой:
Из общего выражения для сферических функций сразу следует закон преобразования:
Следовательно,  - собственные функции оператора четности - собственные функции оператора четности 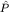 , принадлежащие собственному значению +1(-1) при четном (нечетном) , принадлежащие собственному значению +1(-1) при четном (нечетном)  . .
Общая структура сферических функций такова:
Приведем несколько частных значений:
Замечание. Сферические функции связаны с гармоническими полиномами степени  по x,y,z соотношением по x,y,z соотношением
При заданном  имеем имеем 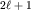 линейно независимых полиномов. Как известно, гармоническая функция по определению удовлетворяет уравнению Лапласа: линейно независимых полиномов. Как известно, гармоническая функция по определению удовлетворяет уравнению Лапласа:
В нашем случае это легко проверяется с использованием выражения оператора Лапласа через  , которое выводится ниже (см. п. 9): , которое выводится ниже (см. п. 9):
Приведем пример. Пусть  . Тогда получаем три гармонических полинома h1m=rY1m, . Тогда получаем три гармонических полинома h1m=rY1m,  : :
Сферические функции  реализуют неприводимое реализуют неприводимое  -мерное представление группы вращений SO(3), образуя базис в пространстве функций, заданных на сфере единичного радиуса. -мерное представление группы вращений SO(3), образуя базис в пространстве функций, заданных на сфере единичного радиуса.
Покажем теперь, что целочисленность  следует из более слабого требования, чем однозначность волновой функции. В общей теории момента фундаментальную роль играют соотношения (см. выше) следует из более слабого требования, чем однозначность волновой функции. В общей теории момента фундаментальную роль играют соотношения (см. выше)
Отсюда следует
В рассматриваемом случае орбитального момента получаем
Покажем, что это соотношение не выполняется, если  - четное целое число. Для этого удобно использовать декартовы координаты, в которых имеем: - четное целое число. Для этого удобно использовать декартовы координаты, в которых имеем:
Заметим, что для произвольной функции f(r),  имеем имеем . Далее сделаем комплексную замену переменных: . Далее сделаем комплексную замену переменных:
В результате приходим к соотношению
Оно должно выполняться тождественно, что невозможно при целом  . Следовательно, . Следовательно,  - целое число. Более подробное рассмотрение показывает, что для полуцелых - целое число. Более подробное рассмотрение показывает, что для полуцелых  операторы момента операторы момента  оказываются неэрмитовыми, т.е. не могут быть наблюдаемыми. оказываются неэрмитовыми, т.е. не могут быть наблюдаемыми.
Назад | Вперед
Посмотреть комментарии[1]
|

