Научная Сеть >> Основы квантовой механики

Наука >> Физика >> Теоретическая физика >> Квантовая механика | Курсы лекций

См. также

Проект Краткая Энциклопедия "Физика" (Вопросы и ответы): 1301

Открытие неклассической логики поведения квантовых объектов - одно из удивительных достижений современной физики: Об интерпретациях классической и квантовой теорий

Утро квантовой эры. Три четверти века назад появилось нестационарное уравнение Шредингера.

О лженауке, ее последствиях и об ошибках в науке

Зонная структура электронного энергетического спектра в твердых телах. Модели свободных и сильно связанных электронов.: ref2

75 лет волновой механике и стационарному уравнению Шредингера.

Наноэлектроника - основа информационных систем XXI века: Квантовые основы наноэлектроники

Открытие неклассической логики поведения квантовых объектов - одно из удивительных достижений современной физики: ref2

11 января - день рождения Д.И. Блохинцева

Векторное пространство

Квантовые ямы, нити, точки. Что это такое?: Классические и квантовые законы движения электронов

Первый в мире и в России журнал о квантовых компьютерах!

Горячие ядра и фазовый переход жидкость-газ в ядерном веществе: Введение

Новая ситуация в квантовой механике (о возможностях управления спектрами, рассеянием, распадами)

Соотношение неопределенностей или принцип дополнительности?

Мировая линия Гамова

Алгебраический подход в квантовой теории поля

Законы физики в космосе

Основы квантовой механики.

А.В. Борисов (Физический факультет МГУ)
Физический факультет МГУ, 1998 г.

Содержание

Движение в центрально-симметричном поле

Рассмотрим движение частицы в стационарном поле $U=U(r),\; r=|{\bf r}|=\sqrt{{x^2+y^2+z^2}}$ . Такое поле называется центрально-симметричным, или, коротко, центральным. В этом случае гамильтониан

$\hat H=\frac{{\bf p}^2}{2m_e}+U(r)$

коммутирует с оператором орбитального момента:

$[\hat H,\hat {\bf L}]=0.$

Покажем это подробнее, получив следующее представление оператора квадрата импульса:

${\bf \hat p}^2=-\hbar^2\nabla^2=-\frac{\hbar^2}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right)+\frac{{\bf\hat L}^2}{r^2}.$

Имеем:

${\bf \hat L^2=(r\times\hat p)^2=-(\hat p\times r)\cdot(r\times\hat p)=-\hat p\cdot(r\times(r\times\hat p))=-\hat p\cdot(r(r\cdot\hat p)}-r^2{\bf\hat p}).$

Из фундаментального соотношения $[\hat p_n,x_m]=-i\hbar\delta_{nm}$ следуют коммутаторы

$[{\bf \hat p\cdot r, r\cdot \hat p}]=-3i\hbar,\; [{\bf\hat p},r^2]=-2i\hbar{\bf r},$

используя которые, находим

${\bf\hat L}^2=r^2{\bf \hat p}^2-({\bf r\cdot \hat p})^2+i\hbar{\bf r\cdot\hat p}.$

Далеe:

${\bf r\cdot\hat p}=-i\hbar{\bf r\cdot\nabla}=-i\hbar r\frac{\partial}{\partial r},\; ({\bf r\cdot\hat p})^2=-\hbar^2\left(r\frac{\partial}{\partial r}+r^2\frac{\partial^2}{\partial r^2}\right).$

В итоге получаем приведенное выше выражение для ${\bf \hat p}^2$ , откуда сразу видно, что $[{\bf \hat L,\hat p^2}]=0$ .
Стационарное уравнение Шредингера 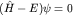$(\hat H-E)\psi=0$ для частицы в центральном поле принимает вид:

$\left[-\frac{\hbar^2}{2m_e r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial}{\partial r}\right)+\frac{{\bf\hat L^2}}{2m_er^2}+U(r)\right]\psi=E\psi.$

Так как момент ${\bf\hat L}$ - интеграл движения, то любая собственная функция гамильтониана представляется в виде произведения радиальной функции, зависящей только от r, и сферической функции (см. п. 7):

$\psi(r,\theta,\varphi)=R(r)Y_l^m(\theta,\varphi),$

т.е. является собственной функцией полного набора наблюдаемых (спин мы не учитываем) $\hat H,{\bf \hat L^2}, \hat L_z$ .
Для радиальной функции получаем уравнение

$\left[-\frac{\hbar^2}{2m_e r^2}\frac{d}{dr}\left(r^2\frac{d}{dr}\right)+\frac{\hbar^2\ell(\ell+1)}{2m_e r^2}+U(r)\right]R=ER.$

Удобно ввести новую функцию согласно

$R(r)=\frac{\chi(r)}{r}.$

Она удовлетворяет радиальному уравнению Шредингера:

$\left[-\frac{\hbar^2}{2m_e}\frac{d^2}{dr^2}+U_\ell(r)\right]\chi=E\chi,$

где введен эффективный потенциал

$U_\ell(r)=U(r)+\frac{\hbar^2\ell(\ell+1)}{2m_er^2}.$

Мы получили уравнение Шредингера для движения частицы на полупрямой $(0\le r \lt \infty)$ в потенциальном поле $U_\ell(r)$ .
Замечание. Даже для свободной частицы (U=0) в состоянии с заданным моментом эффективный потенциал отличен от нуля при 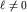$\ell\ne 0$ и совпадает с центробежным потенциалом $\hbar^2\ell(\ell+1)/2m_e r^2$ .
Условие нормировки для $\chi(r)$ совпадает с условием нормировки одномерной волновой функции в силу ортонормированности сферических функций:

$\int d^3 x|\psi|^2=\int\limits_{0}^{\infty}drr^2|R|^2=\int\limits_{0}^{\infty}dr|\chi|^2=1.$

Для физических приложений интерес представляют потенциалы, для которых выполняется условие

$r^2 U(r)\to 0$ при $r\to 0,$

т.е. не более сингулярные, чем $1/r^{2-\varepsilon},\; \varepsilon \gt 0$ , . Спектр радиального гамильтониана

$\hat H_\ell=-\frac{\hbar^2}{2m_e}\frac{d^2}{dr^2}+U(r)+\frac{\hbar^2\ell(\ell+1)}{2m_e r^2}$

хорошо изучен для широкого класса потенциалов U(r).
Выясним асимптотику радиальной функции $\chi(r)$ при $r\to 0$ . Оставляя наиболее сингулярный член в радиальном УШ, получаем:

$\chi''-\ell(\ell+1)r^{-2}\chi=0.$