Пусть две наблюдаемых 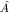 и и 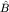 не коммутируют. Тогда их коммутатор имеет вид: не коммутируют. Тогда их коммутатор имеет вид:
где  - эрмитов оператор. Покажем, что дисперсии наблюдаемых в произвольном состоянии - эрмитов оператор. Покажем, что дисперсии наблюдаемых в произвольном состоянии  удовлетворяют ограничению удовлетворяют ограничению
Оно называется соотношением неопределенностей и получено впервые Гейзенбергом (W. Heisenberg) в 1927 г. для частного случая наблюдаемых  и и 
Его общее доказательство принадлежит Вейлю (H. Weyl). Введем наблюдаемые
и рассмотрим неотрицательную функцию действительного параметра 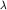 : :
Ввиду произвольности 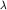 дискриминант полученного квадратного трехчлена должен быть неположительным: дискриминант полученного квадратного трехчлена должен быть неположительным:
С учетом равенства  получаем отсюда приведенное выше соотношение неопределенностей (СН). получаем отсюда приведенное выше соотношение неопределенностей (СН).
Для коммутирующих наблюдаемых правая часть СН обращается в нуль, что соответствует, как мы видели выше (см. п. 3), одновременной измеримости таких наблюдаемых.
Для некоммутирующих наблюдаемых СН накладывает ограничение на точности, с которыми могут быть одновременно заданы (измерены) эти наблюдаемые. Наиболее сильное ограничение имеется в случае, когда ![$(\psi,[\hat A,\hat B]\psi)\ne 0$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula686.gif) для любых состояний для любых состояний  , например, если , например, если ![$[\hat A,\hat B]=ic\hat I,$](http://images.nature.web.ru/nature/2001/02/21/0001161226/tex/formula687.gif) где c=const. В этом случае не существует состояний, в которых обе наблюдаемых имеют определенные значения. где c=const. В этом случае не существует состояний, в которых обе наблюдаемых имеют определенные значения.
Пример. Пусть  Тогда Тогда
и мы получаем соотношение неопределенностей Гейзенберга:
Качественно СН может быть получено из анализа эволюции волнового пакета (см. п. 2). Было показано, что эффективные размеры пакета в координатном и импульсном представлениях, т.е. неопределенности координаты и импульса частицы, связаны соотношением  или или  так как импульс так как импульс 
Детальный анализ показывает, что в случае некоммутирующих наблюдаемых 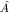 и и 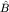 и измерение одной из них приводит к неконтролируемому изменению другой наблюдаемой. Возмущение системы в процессе измерения конечно и таково, что всегда выполняются СН. Иными словами, для точного измерения таких наблюдаемых требуются несовместимые измерительные приборы. и измерение одной из них приводит к неконтролируемому изменению другой наблюдаемой. Возмущение системы в процессе измерения конечно и таково, что всегда выполняются СН. Иными словами, для точного измерения таких наблюдаемых требуются несовместимые измерительные приборы.
Найдем состояния  , в которых достигается минимум неопределенностей,т.е. точное равенство в СН. Получаем для них систему уравнений (см. выше вывод СН): , в которых достигается минимум неопределенностей,т.е. точное равенство в СН. Получаем для них систему уравнений (см. выше вывод СН):
Отсюда находим
и уравнение для определения состояния, минимизирующего произведение неопределенностей, принимает вид:
Рассмотрим случай координаты и импульса:
В координатном представлении  и получаем уравнение: и получаем уравнение:
Здесь 
Нормированное решение имеет вид:
В этом состоянии
СН "координата-импульс" выражает отсутствие точной траектории у частицы. В частности, нельзя определить импульс в данной точке пространства (как в классической механике): импульс характеризует состояние квантовой частицы в целом. Он может быть измерен, например, путем анализа дифракционной картины, образуемой при прохождении пучка частиц через периодическую структуру, с помощью дебройлевского соотношения между длиной волны и импульсом:  Мы ввели основные понятия квантовой механики и можем теперь явно сформулировать, следуя Дж. фон Нейману (J. von Neumann), ее основные постулаты:
Состояния системы описываются ненулевыми векторами
Мы ввели основные понятия квантовой механики и можем теперь явно сформулировать, следуя Дж. фон Нейману (J. von Neumann), ее основные постулаты:
Состояния системы описываются ненулевыми векторами  комплексного сепарабельного гильбертова пространства H, причем векторы комплексного сепарабельного гильбертова пространства H, причем векторы  и и  описывают одно и то же состояние тогда и только тогда, когда описывают одно и то же состояние тогда и только тогда, когда  , где c - произвольное комплексное число. Каждой наблюдаемой однозначно сопоставляется линейный эрмитов оператор , где c - произвольное комплексное число. Каждой наблюдаемой однозначно сопоставляется линейный эрмитов оператор  Наблюдаемые одновременно измеримы тогда и только тогда, когда соответствующие им эрмитовы операторы коммутируют.
Наблюдаемые одновременно измеримы тогда и только тогда, когда соответствующие им эрмитовы операторы коммутируют.
В результате измерения наблюдаемой, представляемой оператором  может быть получено лишь одно из собственных значений может быть получено лишь одно из собственных значений 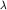 оператора оператора  Вероятность wn получить значение Вероятность wn получить значение  при измерении в состоянии при измерении в состоянии  равна равна
где cn - коэффициент в разложении  по полной системе собственных функций по полной системе собственных функций  оператора оператора 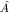 : :
Эволюция системы определяется уравнением Шредингера
где 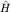 - гамильтониан.
Каждому вектору - гамильтониан.
Каждому вектору  из пространства H отвечает некоторое состояние системы, любой эрмитов оператор из пространства H отвечает некоторое состояние системы, любой эрмитов оператор 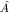 соответствует некоторой наблюдаемой. соответствует некоторой наблюдаемой.
Рассмотренный в п. 3 принцип суперпозиции, как легко проверить, следует из постулата П4.
Замечание 1. Выбор пространства H и закона соответствия  для конкретной физической системы определяется согласием предсказаний теории с результатами эксперимента. Этот выбор не может быть формализован: можно построить бесконечно много квантовых теорий, которые в пределе для конкретной физической системы определяется согласием предсказаний теории с результатами эксперимента. Этот выбор не может быть формализован: можно построить бесконечно много квантовых теорий, которые в пределе  переходят в одну и ту же классическую теорию. переходят в одну и ту же классическую теорию.
Замечание 2. Существуют правила суперотбора, согласно которым пространство состояний H разбивается в прямую сумму ортогональных подпространств, причем сумма векторов из разных подпространств не может соответствовать физически реализуемому состоянию. Например, запрещена суперпозиция состояний с различными электрическими зарядами.
Назад | Вперед
Посмотреть комментарии[1]
|

