Научная Сеть >> Основы квантовой механики

Наука >> Физика >> Теоретическая физика >> Квантовая механика | Курсы лекций

См. также

Проект Краткая Энциклопедия "Физика" (Вопросы и ответы): 1301

Открытие неклассической логики поведения квантовых объектов - одно из удивительных достижений современной физики: Об интерпретациях классической и квантовой теорий

Утро квантовой эры. Три четверти века назад появилось нестационарное уравнение Шредингера.

О лженауке, ее последствиях и об ошибках в науке

Зонная структура электронного энергетического спектра в твердых телах. Модели свободных и сильно связанных электронов.: ref2

75 лет волновой механике и стационарному уравнению Шредингера.

Наноэлектроника - основа информационных систем XXI века: Квантовые основы наноэлектроники

Открытие неклассической логики поведения квантовых объектов - одно из удивительных достижений современной физики: ref2

11 января - день рождения Д.И. Блохинцева

Векторное пространство

Квантовые ямы, нити, точки. Что это такое?: Классические и квантовые законы движения электронов

Первый в мире и в России журнал о квантовых компьютерах!

Горячие ядра и фазовый переход жидкость-газ в ядерном веществе: Введение

Новая ситуация в квантовой механике (о возможностях управления спектрами, рассеянием, распадами)

Соотношение неопределенностей или принцип дополнительности?

Мировая линия Гамова

Алгебраический подход в квантовой теории поля

Законы физики в космосе

Основы квантовой механики.

А.В. Борисов (Физический факультет МГУ)
Физический факультет МГУ, 1998 г.

Содержание

Гармонический осциллятор

Осциллятор в классической механике

Гармоническим осциллятором (ГО) в классической механике называется система, описываемая гамильтонианом (см. выше п. 1)

$H=\frac{1}{2m}p_x^2+\frac{m\omega^2}{2}x^2.$

Уравнение движения

$\ddot x+\omega^2 x=0$

имеет общее решение

$x(t)=A\cos(\omega t+\theta),$

где A и $\theta$ - произвольные постоянные. Оно описывает гармонические колебания частицы около положения равновесия x=0. Энергия осциллятора - интеграл движения,

$E=\frac{1}{2}m\omega^2 A^2={\rm const},$

и принимает произвольные неотрицательные значения.
К ГО сводится задача о движении частицы в потенциальном поле U(q) при условии, что потенциал имеет локальный минимум в точке q=q₀, и в ее малой окрестности справедливо разложение:

U(q)=U(q₀)+1/2 U''(q₀)(q-q₀)²+...

Введя новую координату x=q-q₀ и обозначив $U''(q_0)=m\omega^2 \gt 0,$ получим потенциал ГО при условии, что энергия частицы E близка к U(q₀), так что можно пренебречь высшими членами разложения по x. При этом всегда можно положить U(q₀)=0 ввиду произвола выбора начала отсчета энергии.
Заметим, что ГО - простая модель, описывающая приближенно колебания атомов в молекулах, в твердых телах (вблизи узлов кристаллической решетки), колебания поверхности атомных ядер и др. Однако для таких задач классическая теория неприменима.

Стационарные состояния осциллятора

В квантовой механике ГО отвечает оператор Гамильтона

$\hat H=\frac{1}{2m}\hat p_x^2+\frac{1}{2}m\omega^2\hat x^2,\; [\hat x,\hat p_x]=i\hbar.$

Рассмотрим стационарные состояния ГО, используя координатное представление $(\hat x=x,\; \hat p_x=-i\hbar \partial/\partial x):$

$\psi(t,x)={\rm exp}\left(-\frac{i}{\hbar}Et\right)\varphi(x).$

Стационарное уравнение Шредингера $(\hat H-E)\varphi=0$ принимает вид:

$\frac{d^2\varphi}{dx^2}+\frac{2m}{\hbar^2}\left(E-\frac{m}{2}\omega^2 x^2\right)\varphi=0.$

Удобно ввести безразмерные координату и параметр:

$\xi=\frac{x}{x_0},\; \lambda=\frac{2E}{\hbar\omega},$

где характерная длина

$x_0=\sqrt{\frac{\hbar}{m\omega}}.$

Тогда получим уравнение

$\varphi''+(\lambda-\xi^2)\varphi=0.$

Найдем сначала асимптотику решения $\varphi_\infty$ при $|\xi|\to\infty:$

$\varphi''-\xi^2\varphi\cong 0,\; \varphi\cong\varphi_\infty=C_1 e^{-\xi^2/2}+C_2 e^{\xi^2/2}.$

Потребуем выполнения условия $\|\varphi\| \lt \infty,$ что соответствует финитному движению в классической механике. Тогда решение УШ должно иметь вид:

$\varphi= e^{-\xi^2/2}v(\xi),$

где v - полином конечного порядка по $\xi.$ Для $v(\xi)$ получаем уравнение

$v''-2\xi v'+(\lambda-1)v=0.$

Ищем его решение в виде степенного ряда:

$v=\sum\limits_{k=0}^{\infty}c_k\xi^k.$

Подставив ряд в уравнение и сделав очевидные замены индекса суммирования, находим:

$\sum\limits_{k=0}^{\infty}\xi^k[(k+2)(k+1)c_{k+2}+(\lambda-1-2k)c_k]=0.$

Отсюда следует рекуррентное соотношение для коэффициентов ряда:

$c_{k+2}=\frac{2k+1-\lambda}{(k+1)(k+2)}c_k.$

Ряд превращается в полином только при

$\lambda=2n+1,\; n=0,1,2,\ldots.$

Следовательно, энергия осциллятора $E=\lambda\hbar\omega/2$ должны быть квантованной:

$E_n=\hbar\omega\left(1+\frac{1}{2}\right).$

Заметим, что

$E_n\ge E_0=\frac{1}{2}\hbar\omega \gt 0.$

В классической же теории E_min=0. Напомним (см. п. 1), что согласно первоначальному постулату квантования Планка $E_n=n\hbar\omega.$
Рассмотрим собственные функции $\varphi_n(x).$ Полученное выше рекуррентное соотношение связывает коэффициенты при степенях $\xi$ одинаковой четности. Это не случайно: гамильтониан ГО - четная функция x, $\hat H(-x)=\hat H(x).$ Поэтому $\varphi_n(x)$ и $\varphi_n(-x)$ принадлежат одному и тому же собственному значению E_n. Но в одномерном случае вырождение, как известно, отсутствует, т.е. $\varphi_n(-x)=C\varphi_n(x),$ C=const. Учитывая, что произвольная функция всегда может быть представлена в виде суммы четной и нечетной функций:

$\varphi(x)=\varphi_+(x)+\varphi_-(x),\; \varphi_\pm(x)=\frac{1}{2}[\varphi(x)\pm \varphi(x)]=\pm\varphi_\pm(-x),$

получаем, что собственные функции должны быть определенной четности. Формально это означает существование оператора четности 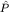$\hat P$ :

$\hat P\varphi(x)=\varphi(-x),\; \hat P^2=\hat I,$

коммутирующего с гамильтонианом, $[\hat H,\hat P]=0.$ Его собственными функциями являются $\varphi_\pm(x):\; \hat P\varphi_\pm(x)=\pm\varphi_\pm(x).$
В рассматриваемом случае ГО из рекуррентных соотношений следует, что четность $\varphi_n(x)$ совпадает с четностью n:

$\varphi_n(-x)=(-1)^n \varphi_n(x).$

Полагая $c_0\ne 0,$ c₁=0 получим четные собственные функции, а при c₀=0, $c_1\ne 0$ - нечетные.
Нормированные волновые функции стационарных состояний ГО имеют вид (их вывод мы дадим ниже простым алгебраическим методом):

$\varphi_n(x)=(\sqrt{\pi}2^n n! x_0)^{-1/2}H_n(\xi) e^{-\xi^2/2}.$

Здесь введены полиномы Эрмита:

$H_n(\xi)=(-1)^n e^{\xi^2}\frac{d^n}{d\xi^n}e^{-\xi^2}.$

В частности,

$H_0=1,\; H_1=2\xi,\; H_2=4\xi^2-2,\; H_3=8\xi^3 -12\xi.$

Покажем теперь, что ненулевое минимальное собственное значение энергии осциллятора E₀ прямо следует из соотношения неопределенностей. В стационарных состояниях <x>=0, <p_x>=0 в силу определенной четности волновых функций, и СН принимает вид

$\left \lt x^2\right \gt \left \lt p_x^2\right \gt \ge\frac{\hbar^2}{4}.$

Поэтому для энергии в таких состояниях имеем:

$E= \lt \hat H \gt =\frac{1}{2m}\left \lt p_x^2\right \gt +\frac{1}{2}m\omega^2 \left \lt x^2\right \gt \ge \frac{\hbar^2}{8m\left \lt x^2\right \gt }+\frac{1}{2}m\omega^2\left \lt x^2\right \gt \equiv f\left(\left \lt x^2\right \gt \right).$

Условие минимума функции f дает:

$f'=-\frac{\hbar^2}{8m\left \lt x^2\right \gt }+\frac{1}{2}m\omega^2=0,\; \left \lt x^2\right \gt _{min}= \frac{\hbar}{2m\omega}=\frac{1}{2}x_0^2.$

В результате

$E_{min}=E_0=\frac{1}{2}\hbar\omega,$

как и должно быть.
Как уже отмечалось, ГО моделирует колебания атомов в кристаллической решетке. Фундаментальный вывод квантовой механики о том, что в основном состоянии осциллятора энергия $E_0\ne 0,$ был подтвержден в экспериментах по рассеянию рентгеновского излучения в кристаллах при низких температурах (R.W. James, E.M. Firth, 1927). В отсутствие колебаний решетки (как это следует из классической теории в пределе нулевой температуры) рассеяния бы не было, но эксперимент его обнаружил. При этом экстраполяция результатов к нулевой температуре показала, что интенсивность рассеяния имеет конечный предел.

Назад | Вперед

MMOnline

Посмотреть комментарии[1]