Next: 6. Примеры NP-полных задач
Up: Сложность вычислительных задач
Previous: 4.2. Класс
Contents: Содержание
5. Набросок доказательства теоремы
Кука-Левина
1) Это утверждение почти очевидно. Советник сообщает Исполнителю
значения переменных, входящих в формулу, при которых она истинна.
Исполнитель справится с проверкой истинности полученного высказывания
за полиномиальное время.
2) Пусть функция из
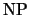 , которую нужно свести к , которую нужно свести к  , имеет вид , имеет вид
 . .
Рассмотрим машину Тьюринга, вычисляющую
 за полиномиальное время. Нам нужно записать в виде
логической формулы условие того, что при некотором
за полиномиальное время. Нам нужно записать в виде
логической формулы условие того, что при некотором  (и заданном
входе (и заданном
входе 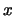 ), машина выдает результат 1.
Для этого представим весь процесс вычисления, длящегося время ), машина выдает результат 1.
Для этого представим весь процесс вычисления, длящегося время
 и использующего память и использующего память
 ,
таблицей вычисления размера ,
таблицей вычисления размера  , показанной на
рисунке 1. , показанной на
рисунке 1.
Рис. 1.
 |
Строка с номером  таблицы задает состояние МТ после таблицы задает состояние МТ после  тактов
работы.
Символы тактов
работы.
Символы  , записанные в таблице,
принадлежат алфавиту , записанные в таблице,
принадлежат алфавиту
 .
Символ .
Символ  определяет пару
(символ, записанный в определяет пару
(символ, записанный в  -й ячейке после -й ячейке после  тактов работы;
состояние управляющего устройства после тактов работы;
состояние управляющего устройства после  тактов работы, если головка
находится над тактов работы, если головка
находится над  -й ячейкой, в противном случае второй элемент
пары - -й ячейкой, в противном случае второй элемент
пары -  ).
Для простоты также считаем, что если
вычисление заканчивается при
некотором входе за ).
Для простоты также считаем, что если
вычисление заканчивается при
некотором входе за  тактов, то строки c номерами, большими тактов, то строки c номерами, большими
 , повторяют строку с номером , повторяют строку с номером  . .
Состояние каждой
клетки таблицы можно закодировать конечным (не зависящим от 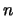 ) числом
булевых переменных. Имеются локальные правила согласования,
т. е. состояние каждой клетки ) числом
булевых переменных. Имеются локальные правила согласования,
т. е. состояние каждой клетки  в строке ниже нулевой
однозначно определяется состояниями клеток в предыдущей строке, лежащих
непосредственно над данной ( в строке ниже нулевой
однозначно определяется состояниями клеток в предыдущей строке, лежащих
непосредственно над данной ( ), левее данной ( ), левее данной ( )
и правее данной ( )
и правее данной ( ).
Каждое такое
условие можно записать в виде логической формулы от переменных,
кодирующих состояния клеток, причем размер этой формулы от ).
Каждое такое
условие можно записать в виде логической формулы от переменных,
кодирующих состояния клеток, причем размер этой формулы от 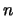 также не
зависит. также не
зависит.
Еще нам нужно записать условие успешности вычисления (результат
равен 1). Для этого заметим, что
без ограничения общности можно
считать, что состояния клеток таблицы кодируются так, что одна из
кодирующих переменных равна 1 только в том случае, когда в ячейке
записана 1. Тогда значение этой переменной для кода  и
будет результатом вычисления. и
будет результатом вычисления.
Определим формулу  как
конъюнкцию всех формул, в которые подставлены значения переменных,
кодирующих вход как
конъюнкцию всех формул, в которые подставлены значения переменных,
кодирующих вход  , дополненный символами , дополненный символами
 до длины до длины
 .
Значения, соответствующие .
Значения, соответствующие 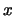 и и 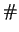 , - константы, поэтому
переменные, от которых зависит эта формула, отвечают , - константы, поэтому
переменные, от которых зависит эта формула, отвечают  и кодам
внутренних ячеек таблицы. Так что можно считать, что формула и кодам
внутренних ячеек таблицы. Так что можно считать, что формула
 зависит
от зависит
от  и еще от каких-то переменных, которые мы обозначим и еще от каких-то переменных, которые мы обозначим  . .
Итак, мы сопоставили слову 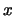 формулу формулу
 , которая
по построению обладает следующим свойством.
Если выполняется , которая
по построению обладает следующим свойством.
Если выполняется  , то найдется такой набор значений , то найдется такой набор значений  ,
при котором ,
при котором
 истинна (эти значения описывают
работу МТ на входе истинна (эти значения описывают
работу МТ на входе  ). А если ). А если  не выполняется, то не выполняется, то
 всегда ложна (поскольку по сути утверждает, что
вычисление на входе всегда ложна (поскольку по сути утверждает, что
вычисление на входе  дает ответ "да").
Таким образом, при дает ответ "да").
Таким образом, при  такая формула иногда (при некоторых
значениях такая формула иногда (при некоторых
значениях  ) истинна, при ) истинна, при  - всегда ложна. - всегда ложна.
Next: 6. Примеры NP-полных задач
Up: Сложность вычислительных задач
Previous: 4.2. Класс
Contents: Содержание
Написать комментарий
|

