Next: 6.2. Разрешимость системы уравнений
Up: 6. Примеры NP-полных задач
Previous: 6. Примеры NP-полных задач
Contents: Содержание
Эта
задача
задается предикатом
| |
 |
|
 |
| 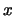 есть 3-КНФ, которая
истинна при некоторых значениях переменных.
3-КНФ - это конъюнкция дизъюнкций, каждая из которых содержит три
литерала, а литерал - это переменная или ее отрицание. есть 3-КНФ, которая
истинна при некоторых значениях переменных.
3-КНФ - это конъюнкция дизъюнкций, каждая из которых содержит три
литерала, а литерал - это переменная или ее отрицание. |
|
| |
 |
|
 |
| 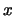 есть 3-КНФ, которая ложна при всех
значениях переменных. есть 3-КНФ, которая ложна при всех
значениях переменных. |
|
| | | | |
|
 также также
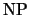 -полна. Это устанавливается сведением к ней -полна. Это устанавливается сведением к ней
 . .
Теорема 2.
 . .
Доказательство.
Рассмотрим вычисление
истинности заданной
формулы
 , использующей связки , использующей связки
 . Результаты промежуточных вычислений
обозначим . Результаты промежуточных вычислений
обозначим
 . Для каждой переменной . Для каждой переменной  выполнено одно из трех равенств
выполнено одно из трех равенств
 |
(7) |
где  либо переменные формулы, либо уже
определенные вспомогательные переменные, т. е. либо переменные формулы, либо уже
определенные вспомогательные переменные, т. е.
 . .
Теперь запишем
3-КНФ, равносильную исходной формуле
 .
В эту КНФ будут входить переменные .
В эту КНФ будут входить переменные
 и и  .
Построим вначале конъюнкцию .
Построим вначале конъюнкцию  условий,
означающих, что каждая из вспомогательных переменных условий,
означающих, что каждая из вспомогательных переменных
 имеет значение, задаваемое формулой (7).
Есть три типа таких условий
и каждый можно записать в виде 3-КНФ: имеет значение, задаваемое формулой (7).
Есть три типа таких условий
и каждый можно записать в виде 3-КНФ:

Подставляя
эти 3-КНФ в  , получим 3-КНФ , получим 3-КНФ  .
Искомая 3-КНФ имеет вид .
Искомая 3-КНФ имеет вид
 . Действительно, истинность . Действительно, истинность
 равносильна утверждению: все присваивания выполнены правильно
и в результате получилась 1 ( равносильна утверждению: все присваивания выполнены правильно
и в результате получилась 1 ( ). Значит, если при
каких-то значениях переменных ). Значит, если при
каких-то значениях переменных 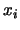 формула формула  истинна, то
3-КНФ истинна, то
3-КНФ  выполнима, и наоборот. выполнима, и наоборот.

Next: 6.2. Разрешимость системы уравнений
Up: 6. Примеры NP-полных задач
Previous: 6. Примеры NP-полных задач
Contents: Содержание
Написать комментарий
|

