Научная Сеть >> М.Н. Вялый "Сложность вычислительных задач"

Наука >> Математика >> Математическое образование | Популярные статьи

Next: 8.3. Up: 8. Класс IP Previous: 8.1. Дополнительные возможности: подбрасывание Contents: Содержание

8.2. Определение класса IP

Класс $\ensuremath{\mathrm {IP}}$ составляют задачи, для которых существуют "интерактивные доказательства правильности ответа". Другими словами, есть интеллектуально всемогущий и пристрастный Советник, к услугам которого разрешено прибегать полиномиально ограниченному вероятностному алгоритму, а задача принадлежит классу $\ensuremath{\mathrm {IP}}$ , если есть такой способ организовать работу пары (Исполнитель с монеткой, Советник), что вероятность правильного результата достаточно высока (больше ).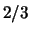

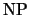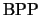Как и в предыдущих случаях, мы хотим привести работу пары наших персонажей к некоторому каноническому виду. Заметим, что теперь, в отличие от класса $\ensuremath{\mathrm {NP}}$ , Советник не знает заранее списка вопросов, которые ему будут заданы: эти вопросы определяются, помимо прочего, подбрасыванием монетки. Однако, как и в случае класса $\ensuremath{\mathrm {BPP}}$ , Исполнитель может составлять таблицы случайных битов и пользоваться ими.

Будем считать, что Советник видит результаты подбрасывания монетки. Поэтому со стороны Исполнителя было бы неосмотрительно составлять таблицу случайных битов на все время диалога с Советником. Однако он ничего не теряет в возможности контролировать Советника, если такая таблица составляется перед каждым вопросом. А Советник, глядя на таблицу, уже может понять, какой именно вопрос задаст ему Исполнитель, сообщить Исполнителю этот вопрос и свой ответ на него.

Поэтому работу пары (Исполнитель с монеткой, Советник) можно преобразовать (с незначительной потерей ресурсов) к следующему каноническому виду: Исполнитель составляет таблицу случайных битов, показывает ее Советнику, тот говорит нечто в ответ и т. д. Количество таких раундов ограничено заранее заданным полиномом от длины входного слова. После завершения диалога с Советником, Исполнитель по записи этого диалога принимает решение. Вероятность правильного ответа (доля диалогов, приводящих к правильному ответу) должна быть достаточно велика. Все эти неформальные соображения учтены в следующем определении, в котором 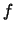- характеристическая функция.

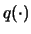Определение 8. $f\in\ensuremath{\mathrm {IP}}$ означает, что есть такие полиномиально вычислимая (характеристическая) функция (Исполнитель), некоторая функция (Советник) и полиномы $q(\cdot)$ (длина таблицы случайных чисел), $s(\cdot)$ (длина диалога), что $\vert P(u)\vert=\mathop{\mathrm{poly}}\nolimits (\vert u\vert)$ (Советник дает полиномиально ограниченные советы) и для каждого 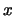доля тех двойных последовательностей

$\begin{displaymath} \begin{matrix} r_{11}&r_{12}&\dots&r_{1q(\vert x\vert)}\\ r... ...vert)2}&\dots&r_{s(\vert x\vert)q(\vert x\vert)}, \end{matrix} \end{displaymath}$

для которых

$\begin{displaymath} f(x)=V(x,r_1, P(r_1), r_2, P(r_1,r_2),\dots, r_{s(\vert x\vert)}, P(r_1,r_2,\dots,r_{s(\vert x\vert)})), \end{displaymath}$

больше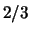

Мы использовали обозначение $r_k=(r_{k1},r_{k2},\dots,r_{kq(\vert x\vert)})$ и естественное соглашение: когда мы применяем функцию к последовательности аргументов, предполагается, что эта последовательность представлена в виде, аналогичном (1) (см. начало статьи).

Замечание 6. Работа Исполнителя в описанном выше формате похожа на работу Судьи из уголовно-процессуальной интерпретации класса $\ensuremath{\mathrm{PSPACE}}$ . Только теперь одна из спорящих сторон - генератор случайных чисел. Теорема 7 получает любопытную интерпретацию: анализ игры против сколь угодно умного противника с вычислительной точки зрения эквивалентен анализу (другой) игры против простейшего противника: генератора случайных чисел5.

Next: 8.3. Up: 8. Класс IP Previous: 8.1. Дополнительные возможности: подбрасывание Contents: Содержание

МЦНМО

Написать комментарий