Научная Сеть >> Малый Мехмат, 24 февраля, 9 класс: Десятичная запись чисел

Наука >> Математика >> Математическое образование >> Математические соревнования | Задачи

Малый Мехмат                      9 класс


Занятие 16               24 февраля 2001 года



Десятичная запись чисел

Для того, чтобы записать натуральное число A в десятичной системе счисления, мы его представляем в виде

A = 10^{n .}a_n + 10^{n - 1 .}a_{n - 1} + ... + 10^.a₁ + a₀,

где a_n, a_{n - 1},..., a₀ -- цифры от 0 до 9, причем a_n 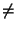$\not=$ 0. При этом цифра единиц a₀ -- это остаток от деления числа A на 10. Рассмотрим примеры задач.
Задача. Между цифрой единиц и цифрой десятков двузначного числа вставили ноль, и оказалось, что полученное число в девять раз больше исходного. Найти исходное число.
Решение. Запишем исходное число в виде 10a + b, где a -- частное, а b -- остаток от деления числа на 10. Теперь заметим, что после того, как мы впишем нуль между цифрой десятков и единиц наше число станет равным 100a + b. Запишем: 9(10a + b) = 100a + b, откуда 10a = 8b, 5a = 4b. Значит, цифра b делится на 5, откуда b = 0 или b = 5. Поскольку a и b -- не нули одновременно, a = 4 и b = 5. Исходное число -- 45.
Задача. Может ли квадрат натурального числа кончаться на 7?
Решение. Пусть число a делится на 10 с остатком r, т. е. r -- последняя цифра a. Тогда число а² делится на 10 с тем же остатком, что и r² (остатки можно умножать). Перебрав все цифры, убеждаемся, что ни у одной из них квадрат не кончается на 7.
Задача 14.8. Докажите, что предпоследняя цифра любой степени тройки четна.
Доказательство будем проводить по индукции.
База: у 3¹ предпоследняя цифра четна (ноль). Шаг: пусть 3ⁿ = 10a + b, где a -- частное, а b -- остаток от деления 3ⁿ на 10. Поскольку b нечетно и не делится на 5, то оно может принимать значения 1, 3, 7 или 9. В любом из этих четырех случаев цифра десятков числа 3b четна (она равна нулю, если b = 1 или 3 и двойке, если b = 7 или 9). Четность предпоследней цифры числа 3ⁿ означает четность числа a. Тогда 3^{n + 1} = 3^.3ⁿ = 3(10a + b) = 30a + 3b. У этого числа цифра единиц такая же, а цифра десятков имеет ту же четность, как и у числа 3b. Значит, цифра десятков четна.

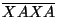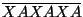а) Докажите, что число $\overline{XAXA}$ делится на 101 (одинаковые буквы обозначают одинаковые цифры, разные буквы -- разные цифры). б) Докажите, что число $\overline{XAXAXA}$ делится на 7.

а) Докажите, что число 111...11 (81 единица) делится на 81. б) Верно ли, что если сумма цифр числа делится на 81, то и оно само делится на 81?

Предпоследняя цифра числа, являющегося точным квадратом, нечетна. Докажите, что последняя цифра равна 6.

Найдите четырехзначное число, являющееся точным квадратом, у которого две первые цифры совпадают и две последние тоже совпадают.

В ряд выписаны в порядке возрастания числа, делящиеся на 9: 9, 18, 27, 36, .... Под каждым числом этого ряда записана его сумма цифр. а) На каком месте во втором ряду впервые встретится число 81? б) Что встретится раньше: четыре раза подряд число 27 или один раз число 36?

Докажите, что степень двойки не может оканчиваться на четыре одинаковые цифры.

Восстановить треугольник по двум его вершинам и прямой, содержащей биссектрису, выходящую из третьей вершины.

На каждом километре шоссе между селами Елкино и Палкино стоит столб с табличкой, на одной стороне которой написано, сколько километров до Елкино, а на другой -- до Палкино. Боря заметил, что на каждом столбе сумма всех цифр равна 13. Каково расстояние от Елкино до Палкино?

Десятичная запись числа начинается с единицы, а если ее перенести в конец записи, то число увеличится в три раза. Найти такое число.

Докажите, что существует бесконечно много таких троек натуральных чисел a, b, c, что a! = b!c! (a, b > 1). (Факториалом n! натурального числа n называется произведение всех натуральных чисел от единицы до него: n! = 1^.2^.3^....^.n).

Alexandr Ryzhov 2001-03-12

МЦНМО

Написать комментарий