ЛОГИЧЕСКИЕ ЗАДАЧИ
Все задачи этого задания взяты из книги Лихтарников Л.М. "Задачи мудрецов" М. "Просвещение" 1996. Книга для учащихся III-IX классов.

---

1. Цвет волос

    Беседуют трое: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: "Любопытно. Что один из нас русый, другой - брюнет, а третий - рыжий, но ни у кого цвет волос не соответствует фамилии". Какой цвет волос имеет каждый из беседующих?

Хочу подсказку

    Решение:
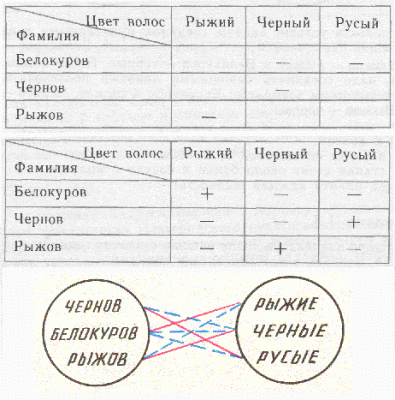
Первое решение Для решения задачи воспользуемся таблицей 3*3. По условию задачи Белокуров не русый, Чернов не брюнет, и Рыжов не рыжий. Это позволяет поставить знак в соответствующих клетках. Кроме того, по условию Белокуров не брюнет, и, значит, в клетке на пересечении строки Белокуров и столбца Черный также нужно поставить знак .
Из таблицы следует, что Белокуров может быть только рыжим. Поставим знак плюс в соответствующей клетке. Отсюда видно, что Чернов не рыжий. Обозначим это знаком минус в таб- лице. Теперь ясно, что Чернов может быть только русым, а Ры- жов брюнетом. Использование таблицы помогло наглядно оформить решение задачи.
Второе решение Будем изображать элементы каждого из множеств точками на плоскости. Если по условию задачи между элементами этих множеств имеет место взаимно однозначное соответствие, то будем соединять сплошной линией те элементы множеств, которые находятся во взаимно однозначном соответствии, и пунктирной линией, если такого соответствия нет. Используя условие задачи, мы можем получить на графике наглядное изображение исходных данных, а далее путем логических рассуждений установить необходимое взаимно однозначное соответствие между остальными элементами этих множеств. Изобразим здесь графически два множества (множество фамилий и множество цветов волос). Используя условие задачи, соединим пунктирными линиями следующие пары элементов: Чернов черные, Белокуров русые, Рыжов рыжие и Белокуров черные. После этого, очевидно, надо соединить сплошными линиями последовательно следующие пары элементов: Белокуров рыжие, Чернов русые, Рыжов черные.

---

3. Шахматный турнир

    В финальном турнире играли пять шахматистов. А окончил все партии вничью. Б сыграл вничью с занявшими первое и последнее место. В проиграл Б, но зато сыграл вничью только одну партию. Г выиграл у Д и у занявшего четвертое место. Д не выиграл ни одной партии.
Кто сколько очков набрал и какое место занял?

Хочу подсказку

Хочу решение

---

2. Строй мальчиков

    При построении восемь мальчиков разместились так, что 1) А был впереди Б и В;
2) Б - впереди К через одного;
3) Л впереди А, но после Д;
4)В - после Е через одного;
5) Д - между Б и Г;
6) Е - рядом с К, но впереди В.
В каком порядке выстроились мальчики?

Хочу подсказку

Хочу решение

---

4. Два стрелка

    Два стрелка произвели по 5 выстрелов, причем поподания были следующие: 10, 9, 9, 8, 8, 5, 4, 4, 3, 2. Первыми тремя выстрелами они выбили одинаковое количество очков, но тремя последними выстрелами первый стрелок выбил втрое больше очков, чем второй.
Сколько очков набрал каждый из них третьим выстрелом?

Хочу подсказку

Хочу решение

---

5*. Шестизначное число - квадрат

    ABCDEF - число из шести цифр. Все они разные, расположенные слева направо в возрастающем порядке. Число это квадрат. Определите, какое это число.

Хочу подсказку

Хочу решение

---

6.Аборигены и пришельцы

    На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы всегда лгут. Путешественник, приехавший на остров, нанял островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал проводника узнать. К какому племени принадлежит этот туземец. Проводник вернулся и сказал: "Туземец говорит, что он абориген". Кем был проводник: пришельцем или аборигеном?

Хочу подсказку

Хочу решение

---

7.Игра на шахматной доске

    Двое мальчиков играют в такую игру: они по очереди ставят ладьи на шахматную доску. Выигрывает тот, при ходе которого все клетки доски оказываются битыми, поставленными фигурами. Кто выигрывает, если оба стараются играть наилучшим образом?

Хочу подсказку

Хочу решение