Все задачи этого занятия взяты из задач :;-ой Московской математической олимпиады, окружного тура, состоявшегося 28 января 2001 года.

---

1. Восемь взвешиваний

    В корзине лежат 13 яблок. Имеются весы, с помощью которых можно узнать суммарный вес любых двух яблок. Придумайте способ выяснить за 8 взвешиваний суммарный вес всех ябдок.

Хочу подсказку

Хочу решение

---

2. Проценты

    Два торговца купили в городе одинаковое количество товара по одной и той же цене и увезли каждый в свою деревню продавать. Первый продавал товар в два раза дороже закупочной цены. Второй сначала поднял цену на 60% и продал четвертую часть товара, затем поднял цену еще на 40% и продал остальную часть товара. Кто из них выручил больше?

Хочу подсказку

Хочу решение

---

3. Путешествие по маршруту Москва-Астрахань.

    Ежедневно в полдень из Москвы в Астрахань и из Астрахани в Москву выходит рейсовый теплоход.Теплоход, вышедший из Москвы, идет до Астрахани ровно четверо суток, затем двое суток стоит, и в полдень, через двое суток после своего прибытия в Астрахань, отправляется в Москву. Теплоход, вышедший из Астрахани, идет в Москву ровно пять суток и, после двухсуточного отдыха в Москве, отправляется в Астрахань. Какое количество теплоходов должно работать на линии Москва - Астрахань - Москва при описанных условиях движения?

Хочу подсказку

Хочу решение

---

4. Расставить корабли в квадрате.

    Можно ли в квадрате 10*10 расставить 12 кораблей 1*4 (для игры типа "морской бой") так, чтобы корабли не соприкасались друг с другом (даже вершинами)?

Хочу подсказку

Хочу решение

---

5. Делимость на 4

    Докажите, что если a, b, c - нечетные числа, то хотя бы одно из чисел ab-1, bc-1, ca-1 делится на 4.

Хочу подсказку

Хочу решение

---

6. Опять система трех уравнений

    Решить систему уравнений:

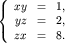
Хочу подсказку

Хочу решение

---

7. Опять квадрат целого числа

    Может ли число, сумма цифр которого равна 2001, быть квадратом целого числа?

Хочу подсказку

Хочу решение