Монохроматическая волна де Бройля (1.1), соответствующая какой-либо частице
с определенными значениями энергии и импульса, описывает одинаковую
вероятность нахождения частицы в любом месте пространства. Монохроматическая
волна не может охарактеризовать движение частицы (например, ее скорость).
Чтобы связать параметр движения - скорость и волновые характеристики
частицы - нужно рассмотреть не строго монохроматическую волну, а группу волн -
волновой пакет. Волновой пакет представляет собой суперпозицию мало отличающихся друг от друга по длине волны и направлению распространения OX монохроматических волн, обладающих близкими частотами. Тогда волну де Бройля 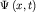 можно представить в виде следующего соотношения: можно представить в виде следующего соотношения:
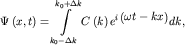 | (1.7) |
где k_{ 0} - волновое число, около которого лежат волновые числа k волн,
образующих группу 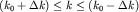 (интервал
(интервал 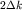 предполагается малым по сравнению с величиной предполагается малым по сравнению с величиной
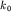 : : 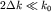 ), ), 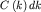 - амплитудный вклад в
волновой пакет волн с волновыми числами, находящимися в бесконечно узком
интервале от k до k +dk. - амплитудный вклад в
волновой пакет волн с волновыми числами, находящимися в бесконечно узком
интервале от k до k +dk.
Результирующая амплитуда такого волнового пакета будет заметно отличаться от
нуля в некоторой небольшой области пространства, которую можно связать с
положением частицы. Покажем, что, амплитудный максимум волнового пакета,
связанный с положением частицы, распространяется в пространстве со
скоростью, равной скорости распространения частицы.
Поскольку, в общем случае, частота волн \omega является функцией
волнового числа, то, используя сформулированное ранее условие 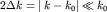 , можно функцию , можно функцию 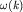 представить в виде разложения в ряд Тейлора около значения представить в виде разложения в ряд Тейлора около значения 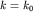 и ограничиться только линейным членом разложения, т.е. записать
и ограничиться только линейным членом разложения, т.е. записать 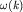 в виде: в виде:
где 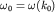 и и  . .
Пусть, для простоты, амплитуда 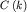 является медленно
меняющейся функцией является медленно
меняющейся функцией 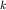 , так что можно принять ее постоянной величиной , так что можно принять ее постоянной величиной
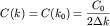 (рис.1 а ). Тогда, произведя в
(1.7) замену переменной (рис.1 а ). Тогда, произведя в
(1.7) замену переменной 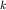 на на 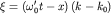 , получим после интегрирования: , получим после интегрирования:
![$ \begin{array}{l} \Psi \left( {\displaystyle x,t} \right) = {\displaystyle \frac{\displaystyle {\displaystyle C_{ 0} }}{\displaystyle {\displaystyle 2\left( {\displaystyle {\displaystyle \omega }'_{ 0} t - x} \right)\Delta k}}}exp{\displaystyle \left[ {\displaystyle \,i\,\left( {\displaystyle \omega _{ 0} t - k_{ 0} x} \right)} \right]} \cdot {\displaystyle \int\limits_{ - \Delta k}^{ + \Delta k} {\displaystyle exp\left( {\displaystyle i\xi } \right)\,} }d\xi = \\ = C\left( {\displaystyle x,t} \right)\,exp{\displaystyle \left[ {\displaystyle \,i\,\left( {\displaystyle \omega _{ 0} t - k_{ 0} x} \right)} \right]} \\ \end{array}$](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula402.gif) | (1.7а) |
Здесь 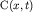 - амплитуда волнового пакета, равная - амплитуда волнового пакета, равная
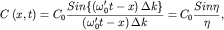 | (1.7б) |
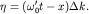
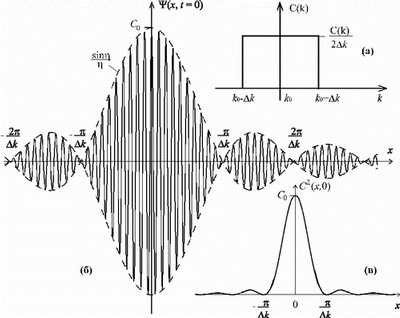 | | Рис. 1. |
Она имеет главный максимум 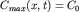 , соответствующий центру группы
волн, в точке , соответствующий центру группы
волн, в точке 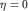 , в которой знаменатель , в которой знаменатель 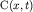 обращается в нуль, то есть при обращается в нуль, то есть при 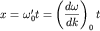 . Отсюда
следует, что центр группы перемещается со скоростью . Отсюда
следует, что центр группы перемещается со скоростью 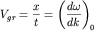 , называемой групповой скоростью, которую можно записать, используя (1.2), в виде : , называемой групповой скоростью, которую можно записать, используя (1.2), в виде :
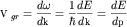 | (1.8) |
Таким образом, скорость частицы-волны (1.8) связана с дисперсией волн, образующих волновой пакет, и определяется быстротой изменения частоты с увеличением волнового вектора. Учитывая зависимость 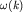 для волн
де Бройля (1.6), групповая скорость для волн
де Бройля (1.6), групповая скорость 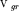 будет равна механической
скорости V частицы: будет равна механической
скорости V частицы:
Следовательно, центр группы волн движется как частица.
На рисунке 1б изображен волновой пакет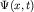 (1.7а) в момент времени (1.7а) в момент времени
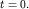
Квадрат амплитуды волнового пакета (1.7б)
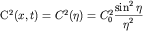 | (1.9) |
пропорционален вероятности нахождения частицы в точке 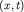 . Из рисунка 1в видно, что область локализации волнового пакета не является точечной, а частица находится с наибольшей вероятностью в
окрестности главного максимума (1.9). Для оценки, область локализации . Из рисунка 1в видно, что область локализации волнового пакета не является точечной, а частица находится с наибольшей вероятностью в
окрестности главного максимума (1.9). Для оценки, область локализации
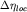 обычно принимают равной половине расстояния между
первыми нулями функции обычно принимают равной половине расстояния между
первыми нулями функции 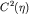 , то есть , то есть 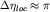 . .
В фиксированный момент времени (например, при 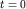 ) условие ) условие 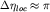 определяет область пространственной
локализации определяет область пространственной
локализации 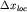 волнового пакета волнового пакета
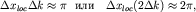 | (1.10) |
или 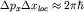 , так как , так как
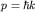 , ,
где 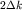 - интервал волновых чисел, составляющих волновой пакет
(1.7). - интервал волновых чисел, составляющих волновой пакет
(1.7).
Положив в условии 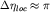 , определяющем
размер волнового пакета, х=сonst (например, , определяющем
размер волнового пакета, х=сonst (например, 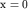 ), при произвольном ), при произвольном  получим
соотношение получим
соотношение
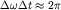 | (1.11) |
или 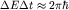 , так как , так как 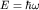 , ,
связывающее временной интервал 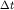 волнового пакета с его спектральной
шириной волнового пакета с его спектральной
шириной 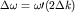 . .
Оба приближенных равенства (1.10) и (1.11) являются следствием
соотношения неопределенностей (соотношения Гейзенберга), открытого в 1927 году немецким физиком
В. Гейзенбергом:
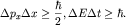
Соотношения неопределенностей устанавливает пределы, за которыми принципы классической физики становятся неприменимыми.
Описывая реальную систему классическими методами и параметрами (координата и
импульс), мы используем некоторое приближение, а соотношение
неопределенности показывает степень его справедливости.
Это означает, что поведение микрочастиц, в частности, электронов в металлах,
нельзя рассматривать на основе классических законов, когда характерные
размеры (межатомное расстояние и размеры кристалла) сравнимы с длиной волны
де Бройля 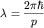 электронов. Реальные
микрочастицы не ведут себя подобно точечным частицам классической физики.
Классическое описание движения микрочастиц с использованием понятий: закон
движения, траектория движения, является лишь приближенным. электронов. Реальные
микрочастицы не ведут себя подобно точечным частицам классической физики.
Классическое описание движения микрочастиц с использованием понятий: закон
движения, траектория движения, является лишь приближенным.
Литература: [Д.И.Блохинцев, 1961,  7, 9, 10, 15, 16] 7, 9, 10, 15, 16]
Назад | Вперед
Написать комментарий
|

