 | | Рис. 6. |
Число электронных состояний dns(E) с заданными
значениями энергий в интервале от Е до (Е+dE)
равно удвоенному (за счет различных направлений спина) числу элементарных
квантовых ячеек (1.21) в p-пространстве в сферическом слое радиуса 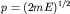 и толщины и толщины 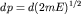 : :
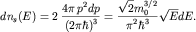 | (2.4) |
Таким образом, плотность состояний 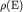 , то есть число разрешенных состояний электронов в единичном интервале
энергии для кристалла единичного объема равна , то есть число разрешенных состояний электронов в единичном интервале
энергии для кристалла единичного объема равна
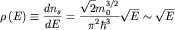 | (2.4а) |
Вид функции 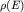 (2.4а) показан на рисунке 7б. (2.4а) показан на рисунке 7б.
Плотность состояний растет с увеличением энергии 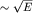 . .
 | | Рис. 7. |
Заполнение этих состояний электронами определяется функцией
распределения Ферми-Дирака (1.16) (см. рис.7а), определяющей вероятность
заполнения электронного состояния с энергией Е:
При Т=0 состояния с Е<ЕF полностью
заполнены, так как f(E<EF)=1, а с
Е>ЕF - пусты. Очевидно, что при Т=0 площадь под
кривой 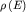 в пределах от 0 до EF(0) дает
полную концентрацию электронов (рис. 7б): в пределах от 0 до EF(0) дает
полную концентрацию электронов (рис. 7б):
 | (2.5) |
При конечной температуре 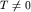 ступенька распределения
f(E) Ферми-Дирака размывается (рис.7а), так что
число частиц ступенька распределения
f(E) Ферми-Дирака размывается (рис.7а), так что
число частиц 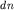 , обладающих энергиями в бесконечно узком интервале
значений от , обладающих энергиями в бесконечно узком интервале
значений от  до до 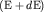 будет равно произведению
плотности состояний (числу состояний в этом интервале
энергий) на вероятность их заполнения: будет равно произведению
плотности состояний (числу состояний в этом интервале
энергий) на вероятность их заполнения:
При этом (рис.7в)
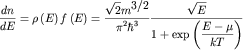 | (2.4б) |
- есть функция плотности заполнения энергетического уровня с энергией
Е при температуре Т. На рисунке 7в представлены зависимости
плотности заполнения 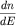 при Т=0 (пунктирная
кривая) и при при Т=0 (пунктирная
кривая) и при 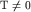 (сплошная кривая). Величина размытости четкой
(при Т=0) границы заполнения энергетических уровней при низких
температурах (так же как и для f(E)) составляет величину \sim
2kT (1.17). (сплошная кривая). Величина размытости четкой
(при Т=0) границы заполнения энергетических уровней при низких
температурах (так же как и для f(E)) составляет величину \sim
2kT (1.17).
При 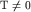 концентрация электронов равна заштрихованной площади на
рис 7в, то есть рассчитывается по формуле: концентрация электронов равна заштрихованной площади на
рис 7в, то есть рассчитывается по формуле:
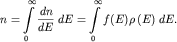 | (2.6) |
Замечание. Функция
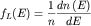 называется функцией распределения электронов по
энергетическим уровням. называется функцией распределения электронов по
энергетическим уровням.
Знание функции заполнения 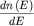 энергетических уровней (или функции распределения по
энергии fL(E)) позволяет рассчитывать средние значения
любых функций от энергии. энергетических уровней (или функции распределения по
энергии fL(E)) позволяет рассчитывать средние значения
любых функций от энергии.
Литература: [А.Н.Матвеев, 1987,  16; Н.Б.Брандт, С.М.Чудинов, 1990, ч.II, гл.1, 16; Н.Б.Брандт, С.М.Чудинов, 1990, ч.II, гл.1,  1, гл.5, 1, гл.5,  1; Дж.Займан, 1966; Ч.Киттель, 1978, гл.7] 1; Дж.Займан, 1966; Ч.Киттель, 1978, гл.7]
Пусть необходимо вычислить среднее значение некоторой функции от энергии
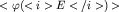 при достаточно низких температурах, то есть для
вырожденного электронного газа при достаточно низких температурах, то есть для
вырожденного электронного газа
По определению среднее значение функции 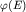 равно равно
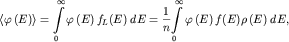 | (2.7) |
где 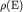 определяется формулой (2.4). определяется формулой (2.4).
Функция распределения Ферми-Дирака f(E) при Т=0
принимает значение либо 0, либо 1 везде за исключением области ступеньки.
При низких температурах, то есть для вырожденного электронного газа,
"ступенька" распределения слабо размыта около 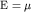 . Этим можно
воспользоваться для упрощения расчетов. . Этим можно
воспользоваться для упрощения расчетов.
Введем для 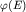 новую функцию новую функцию 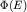 следующим соотношением
следующим соотношением
Выбрав начало отсчета энергии так, чтобы 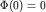 , получим
выражение для , получим
выражение для 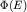 : :
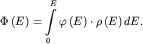 | (2.8) |
Тогда (2.7) можно записать в виде
![$ n{\displaystyle \left\langle {\displaystyle \varphi \left( {\displaystyle E} \right)} \right\rangle } = {\displaystyle \int\limits_{ 0}^{ \infty } {\displaystyle f(E){\displaystyle \frac{\displaystyle {\displaystyle d\Phi \left( {\displaystyle E} \right)}}{\displaystyle {\displaystyle dE}}}\;} }dE = {\displaystyle \left[ {\displaystyle f\left( {\displaystyle E} \right)\Phi \left( {\displaystyle E} \right)} \right]}_{ 0}^{ \infty } - {\displaystyle \int\limits_{ 0}^{ \infty } {\displaystyle \Phi (E){\displaystyle \frac{\displaystyle {\displaystyle df\left( {\displaystyle E} \right)}}{\displaystyle {\displaystyle dE}}}\;} }dE. $](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula708.gif) | (2.9) |
Первый член равен нулю, так как величина f(\infty ) заведомо равна
нулю. График функции
![$ {\displaystyle \frac{\displaystyle {\displaystyle df}}{\displaystyle {\displaystyle dE}}} = - {\displaystyle \frac{\displaystyle {\displaystyle exp\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E - \mu }}{\displaystyle {\displaystyle kT}}}} \right)}}{\displaystyle {\displaystyle kT{\displaystyle \left[ {\displaystyle 1 + exp\left( {\displaystyle {\displaystyle \frac{\displaystyle {\displaystyle E - \mu }}{\displaystyle {\displaystyle kT}}}} \right)} \right]}^{ 2}}}} $](http://images.nature.web.ru/nature/2001/11/16/0001174320/tex/formula709.gif) | (2.10) |
представлен на рисунке 8.
 | | Рис. 8. |
Значение 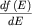 в максимуме составляет в максимуме составляет
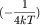 . При отклонении энергии от . При отклонении энергии от  производная
производная 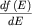 быстро убывает, так что
при быстро убывает, так что
при 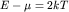 ее значение в 2,4 раза меньше, чем в
максимуме. Это обстоятельство позволяет, разлагая ее значение в 2,4 раза меньше, чем в
максимуме. Это обстоятельство позволяет, разлагая 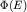 в
ряд Тейлора в окрестности точки в
ряд Тейлора в окрестности точки 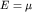 записать выражение (2.9) как записать выражение (2.9) как
Используя соотношение (2.10) для 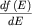 ,
результат интегрирования запишем в виде ,
результат интегрирования запишем в виде
Здесь коэффициенты Сj - определенные интегралы, причем для
нечетных значений j они обращаются в нуль, а для четных значений
j=2n имеем
где 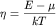 . Вычисление этих сумм - задача
чистой математики, связанная с использованием дзета-функции Римана и чисел
Бернулли. Первые три коэффициента равны . Вычисление этих сумм - задача
чистой математики, связанная с использованием дзета-функции Римана и чисел
Бернулли. Первые три коэффициента равны
Практически чаще всего достаточно одного коэффициента С2.
Поэтому окончательный результат можно записать в виде
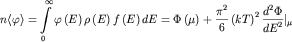 | (2.11) |
где 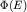 описывается формулой (2.8). описывается формулой (2.8).
Литература: [Дж.Займан, 1966,гл.4,  5] 5]
Назад| Вперед
Написать комментарий
| 
