Рассмотрим теперь случай  когда корни
характеристического уравнения кратные: когда корни
характеристического уравнения кратные:  При этом частота При этом частота  то есть колебания отсутствуют. Общее решение, как нетрудно проверить
подстановкой, имеет следующий вид: то есть колебания отсутствуют. Общее решение, как нетрудно проверить
подстановкой, имеет следующий вид:
 | (1.69) |
где независимые постоянные 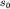 и и  определяются, как и раньше,
начальными условиями. Возможный вид зависимости определяются, как и раньше,
начальными условиями. Возможный вид зависимости 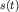 при разных начальных
условиях изображен на рисунке 1.16. при разных начальных
условиях изображен на рисунке 1.16.
 | | Рис. 1.16. |
Их характерной особенностью является то, что они пересекают ось Ot не более
одного раза, и возврат к равновесному состоянию у системы, выведенной из
него, происходит за время порядка нескольких  Такой режим движения
называется критическим. Такой режим движения
называется критическим.
Наконец, если  то общее решение (1.52) является
суммой двух убывающих с течением времени экспонент, поскольку - то общее решение (1.52) является
суммой двух убывающих с течением времени экспонент, поскольку -  Возможный вид зависимостей Возможный вид зависимостей 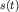 похож на то, что изображено на рис. 1.16, но возврат к равновесию
осуществляется медленнее, чем в критическом режиме, поскольку вязкое трение
больше. Данный режим движения называется апериодическим, или закритическим.
похож на то, что изображено на рис. 1.16, но возврат к равновесию
осуществляется медленнее, чем в критическом режиме, поскольку вязкое трение
больше. Данный режим движения называется апериодическим, или закритическим.
Отметим, что наиболее быстрое возвращение системы к положению равновесия
происходит в критическом режиме, а в колебательном и апериодическом режимах
этот процесс длится дольше. Поэтому, например, гальванометры - приборы для
электрических измерений - работают обычно в режиме, близком к критическому,
когда процесс установления их показаний, то есть смещения s рамки к
устойчивому отклонению  имеет наименьшую длительность (см. рис.
1.17). имеет наименьшую длительность (см. рис.
1.17).
 | | Рис. 1.17. |
Иллюстрацией к рассмотренным закономерностям затухающих колебаний являются
фазовые портреты, построенные для колебательного  а также критического и апериодического
а также критического и апериодического  режимов
(рис. 1.18). режимов
(рис. 1.18).
 | | Рис.1.18. |
При  фазовый портрет представляет собой совокупность
спиралей, стягивающихся в особую точку типа "фокус". На рис. 1.18
изображена одна из таких спиралей. За каждый оборот радиус спирали
уменьшается в фазовый портрет представляет собой совокупность
спиралей, стягивающихся в особую точку типа "фокус". На рис. 1.18
изображена одна из таких спиралей. За каждый оборот радиус спирали
уменьшается в  раз. Для критического и апериодического режимов раз. Для критического и апериодического режимов
 фазовые траектории сходятся в особую точку типа
"узел". фазовые траектории сходятся в особую точку типа
"узел".
На практике мы часто имеем дело с системами, в которых главную роль играет сила сухого трения, не
зависящая от скорости. Типичный пример - пружинный маятник, груз которого
скользит по шероховатой горизонтальной поверхности, или колебательная
система у стрелочных измерительных приборов, основу которой составляет
вращающаяся рамка, испытывающая действие сил сухого трения в оси вращения.
Хотя сила  сухого трения и не меняется по величине, тем не менее
она меняет свое направление при изменении направления скорости. В силу этого
необходимо записать два уравнения сухого трения и не меняется по величине, тем не менее
она меняет свое направление при изменении направления скорости. В силу этого
необходимо записать два уравнения
 | (1.70) |
 | (1.71) |
Если в (1.70) использовать переменную  а в (1.71) - а в (1.71) -  то оба уравнения примут одинаковый вид: то оба уравнения примут одинаковый вид:
 | (1.72) |
Фазовые траектории, соответствующие этому уравнению, представляют собой
эллипсы с центрами, имеющими координаты  для верхней полуплоскости для верхней полуплоскости  и и  для нижней полуплоскости
для нижней полуплоскости  Чтобы нарисовать фазовый портрет,
необходимо сомкнуть фазовые траектории верхней и нижней полуплоскостей на их
общей границе Чтобы нарисовать фазовый портрет,
необходимо сомкнуть фазовые траектории верхней и нижней полуплоскостей на их
общей границе 
Из построенного на рис. 1.19 фазового портрета видно, что движение
прекращается после конечного числа колебаний. Чрезвычайно важно, что система
не обязательно придет к состоянию  а может остановиться, попав в зону
застоя а может остановиться, попав в зону
застоя  Зона застоя тем больше, чем больше сила Зона застоя тем больше, чем больше сила  . Из фазового портрета легко определить убывание амплитуды колебаний за
один период. Это изменение амплитуды в два раза превышает протяженность зоны
застоя:
. Из фазового портрета легко определить убывание амплитуды колебаний за
один период. Это изменение амплитуды в два раза превышает протяженность зоны
застоя:
 | (1.73) |
Таким образом, в отличие от экспоненциального закона (1.56), характерного
для вязкого трения, амплитуда колебаний убывает со временем линейно.
 | | Рис. 1.19. |
На рис. 1.20 показана зависимость от времени смещения колеблющегося тела
при сухом трении. Число совершаемых системой колебаний до их прекращения
зависит от начальной амплитуды  и его можно оценить по формуле: и его можно оценить по формуле:
 | (1.74) |
и зависит от начальной амплитуды  Частота колебаний Частота колебаний  остается такой же, как и при отсутствии силы
трения (см. (1.72)). остается такой же, как и при отсутствии силы
трения (см. (1.72)).
 | | Рис. 1.20. |
Колебания продолжаются до тех пор, пока их амплитуда остается больше
половины ширины зоны застоя  При этом в реальных
условиях колеблющаяся масса останавливается в случайном положении внутри
этой зоны (в точке Р на рис. 1.20). При этом в реальных
условиях колеблющаяся масса останавливается в случайном положении внутри
этой зоны (в точке Р на рис. 1.20).
Назад| Вперед
Посмотреть комментарии[2]
| 
