П.В. Кузьмин (Костромская Государственная Сельскохозяйственная
Академия)
Издательство КГСХА, 2002 г.
| Содержание |
Дополнительно. Из уравнения (39) можно найти зависимость напряжения
на конденсаторе от времени
по фазе совпадает с зарядом.
Сила тока в цепи:
т.е. сила тока через конденсатор опережает по фазе заряд и напряжение на
конденсаторе на 
Напряжение на индуктивности:
т.е. напряжение на индуктивности опережает силу тока на  а напряжение и заряд на конденсаторе на а напряжение и заряд на конденсаторе на 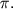 (Это понятно,
ведь в сумме они должны давать ноль, по закону Ома для полной цепи.) (Это понятно,
ведь в сумме они должны давать ноль, по закону Ома для полной цепи.)
Реальным электрическим контуром называется контур с активным сопротивлением отличным от нуля.
Активное сопротивление переводит энергию направленного движения зарядов в энергию хаотического движения.
Т.к. активное сопротивление отлично от нуля, то в таком контуре будут потери
энергии при колебаниях (на выделение тепла при прохождении тока по
проводнику согласно закону Джоуля-Ленца). Амплитуда таких колебаний будет
уменьшаться с течением времени.
Запишем для квазистационарного тока в реальном контуре уравнение,
составленное по закону Ома. (Схема 2.)
 | (40) |
Правая часть уравнения равна нулю, т.к. источников в контуре нет. Тогда
выражение (40) примет вид
 | (41) |
Учитывая, что  уравнение (41) можно привести к
виду уравнение (41) можно привести к
виду
Введем обозначение 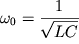 (частота собственных колебаний или
собственная частота) и (частота собственных колебаний или
собственная частота) и 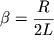 (коэффициент затухания), окончательно получим (коэффициент затухания), окончательно получим
 | (42) |
Сравните с выражением (7). Выражение (42) - это дифференциальное уравнение свободных гармонических затухающих колебаний в электрическом контуре.
 | | Схема 2 |
Из п. 1.2 известно, что решением этого уравнения является функция
 | (43) |
Выражение (43) можно привести к виду
 | (44) |
где начальная амплитуда и начальная фаза равны:
а 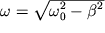 - частота собственных
затухающих колебаний. - частота собственных
затухающих колебаний.
Амплитуда и начальная фаза находятся из начальных условий для заряда и силы тока, а частота собственных незатухающих колебаний и коэффициент затухания - через параметры колебательной системы (индуктивность и электроемкость).
Дополнительно. Из уравнения (44) можно найти зависимость напряжения
на конденсаторе от времени
по фазе совпадает с зарядом .
Сила тока в цепи:
или если умножить и разделить правую часть выражения на 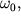 то то
 | (45) |
Если ввести угол, определяемый условиями 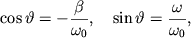 то
выражение (45) можно привести к виду: то
выражение (45) можно привести к виду:
 | (46) |
Значение угла 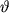 заключено в интервале заключено в интервале 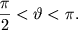 (Из чего можно сделать такой вывод?) Т.о. при наличии в контуре активного
сопротивления сила тока и напряжение на активном сопротивлении опережает по
фазе напряжение на конденсаторе больше, чем на (Из чего можно сделать такой вывод?) Т.о. при наличии в контуре активного
сопротивления сила тока и напряжение на активном сопротивлении опережает по
фазе напряжение на конденсаторе больше, чем на 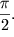
Напряжение на индуктивности:
Проделывая ту же процедуру, что и раньше, получим
 | (47) |
т.е. напряжение на индуктивности опережает силу тока также на угол
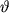 , который изменяется от , который изменяется от 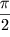 до до 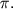
Выражение (47) можно переписать иначе. Учитывая , что  получим получим
 | (48) |
Сравните с напряжением на конденсаторе.
Сумма трех напряжений в любой момент времени должна давать ноль, по закону
Ома для полной цепи. (См. векторную диаграмму 1.)
 | | Векторная диаграмма 1 |
Критическое затухание. Сопротивление, при котором колебательное изменение
параметров системы переходит в апериодическое движение, можно найти из
условия 
Если подставить значения коэффициента затухания и собственной частоты
колебаний, то для величины критического затухания получим
Величина  называется волновое сопротивление последовательного контура. называется волновое сопротивление последовательного контура.
- Частота свободных незатухающих колебаний в электрическом контуре зависит только от индуктивности и электроемкости контура.
- Амплитуда свободных колебаний зависит от начальных условий.
- Если в системе отсутствуют активное сопротивление или им можно пренебречь, то колебания будут незатухающими, т.е. будут продолжаться сколь угодно долго.
- Если в системе достаточно велико активное сопротивление, то колебания будут затухающими, т.е. не будут продолжаться сколь угодно долго. Их амплитуда будет уменьшаться с течением времени.
- Частота свободных затухающих колебаний в электрическом контуре зависит только от индуктивности, электроемкости активного сопротивления контура.
- Амплитуда собственных затухающих колебаний будет убывать со временем по экспоненте, т.к. "сила сопротивления" пропорциональна скорости изменения заряда (первой производной заряда по времени - силе тока).
- Коэффициент затухания зависит от активного сопротивления и индуктивности.
- Если восстанавливающая сила не является линейной функцией смещения системы из положения равновесия, то колебания будут негармоническими. Частота и период будут зависеть от амплитуды колебаний.
Назад| Вперед
Написать комментарий
| 
