Научная Сеть >> Колебания. Краткий конспект лекций.

Наука >> Физика >> Общая физика >> Колебания и волны >> Электрические колебания | Курсы лекций

Написать комментарий

Добавить новое сообщение

См. также

Б.А. Бахметев дипломат, политик, мыслитель

Колебания. Краткий конспект лекций.

П.В. Кузьмин (Костромская Государственная Сельскохозяйственная Академия)
Издательство КГСХА, 2002 г.

Содержание

2.4. Краткие выводы.

Вынужденные колебания возникают в системе под действием внешней периодической силы.
Если внешняя периодическая сила является гармонической (т.е. изменяется по синусу или косинусу), то возникающие колебания будут гармоническими.
Вынужденные колебания происходят с частотой вынуждающей силы, их нельзя возбудить за счет ненулевых начальных условий.
Амплитуда вынужденных колебаний зависит от амплитуды вынуждающей силы, от инерциальных свойств системы и от соотношения частоты вынуждающей силы и собственной частоты колебаний системы.
Наряду с вынужденными колебаниями в системе при наличии ненулевых начальных условий возникают и собственные колебания, которые при наличии сопротивления будут затухающими. Эти колебания происходят с собственной частотой, их амплитуда зависит от начальных условий.
В системе возникают также сопровождающие колебания, которые при наличии сопротивления также будут затухающими. Эти колебания происходят с собственной частотой, но их амплитуда зависит от параметров внешней силы.
При наличии сопротивления все колебания, кроме вынужденных колебаний с течением времени затухнут. Т.е. установившиеся колебания будут вынужденными колебаниями, и будут происходить с частотой вынуждающей силы.
Если частота вынуждающей силы мало отличается от частоты собственных колебаний, а силы сопротивления отсутствуют, то наблюдаются биения - колебания, амплитуда которых медленно изменяется с течением времени по гармоническому закону.
При приближении частоты вынуждающей силы к частоте собственных колебаний наблюдается явление резонанса, которое заключается в резком увеличении амплитуды вынужденных колебаний.
Резонансная частота зависит от параметров вынуждающей силы, инерциальных свойств системы, собственной частоты и коэффициента затухания.
При наличии сопротивления амплитуда координаты, скорости и ускорения достигает максимального значения при различной частоте вынуждающей силы.
При отсутствии сопротивления в случае резонанса амплитуда колебаний монотонно нарастает со временем.
При наличии сопротивления пропорционального скорости, амплитуда колебаний остается конечной величиной.
При действии на систему периодической негармонической силы резонанс возможен, если период возмущающей силы равен или кратен периоду колебаний системы.

3. Энергия механических колебаний

Незатухающие свободные колебания

Для свободных незатухающих колебаний характерно сохранение полной механической энергии в любой момент времени.

Кинетическая энергия пружинного маятника (учитываем, что скорость первая производная координаты по времени)

$E_{k} \left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 2}}}\sin ^{2}\left( {\displaystyle \omega _{0} t + \varphi _{0} } \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 4}}}{\displaystyle \left[ {\displaystyle 1 - \cos \left( {\displaystyle 2\omega _{0} t + 2\varphi _{0} } \right)} \right]}$

(дополнительно использована формула для синуса двойного угла)

Потенциальная энергия деформированной пружины

$E_{p} \left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle kX_{0}^{2} }}{{\displaystyle 2}}}\cos ^{2}\left( {\displaystyle \omega _{0} t + \varphi _{0} } \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 4}}}{\displaystyle \left[ {\displaystyle 1 + \cos \left( {\displaystyle 2\omega _{0} t + 2\varphi _{0} } \right)} \right]}$

(дополнительно использована формула для косинуса двойного угла)

Полная энергия

$E = E_{k} \left( {\displaystyle t} \right) + E_{p} \left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle kX_{0}^{2} }}{{\displaystyle 2}}} = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 2}}} = const.$

Затухающие свободные колебания

При затухающих колебаниях полная энергия системы будет уменьшаться из-за наличия сил сопротивления в системе.

Тогда:

$E_{k} \left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 2}}}e^{ - 2\beta t}\cos ^{2}\left( {\displaystyle \omega t + \varphi _{0} + \vartheta } \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 4}}}e^{ - 2\beta t}{\displaystyle \left[ {\displaystyle 1 + \cos \left( {\displaystyle 2\omega t + 2\varphi _{0} + 2\vartheta } \right)} \right]}$

$E_{p} \left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle kX_{0}^{2} }}{{\displaystyle 2}}}e^{ - 2\beta t}\cos ^{2}\left( {\displaystyle \omega t + \varphi _{0} } \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 4}}}e^{ - 2\beta t}{\displaystyle \left[ {\displaystyle 1 + \cos \left( {\displaystyle 2\omega t + 2\varphi _{0} } \right)} \right]}$

Полная энергия

$E\left( {\displaystyle t} \right) = E_{p} \left( {\displaystyle t} \right) + E_{k} \left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 4}}}e^{ - 2\beta t}{\displaystyle \left[ {\displaystyle 2 + \cos \left( {\displaystyle 2\omega t + 2\varphi _{0} } \right) + \cos \left( {\displaystyle 2\omega t + 2\varphi _{0} + 2\vartheta } \right)} \right]}$

Воспользуемся теоремой сложения косинусов. Получим

$E\left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 4}}}e^{ - 2\beta t}{\displaystyle \left[ {\displaystyle 2 + 2\cos \left( {{\displaystyle \frac{{\displaystyle 2\omega t + 2\varphi _{0} + 2\omega t + 2\varphi _{0} + 2\vartheta }}{{\displaystyle 2}}}} \right) \cdot \cos \left( {{\displaystyle \frac{{\displaystyle 2\omega t + 2\varphi _{0} - \left( {\displaystyle 2\omega t + 2\varphi _{0} + 2\vartheta } \right)}}{{\displaystyle 2}}}} \right)} \right]}$

Преобразуем выражения, являющиеся аргументом косинуса.

$E\left( {\displaystyle t} \right) = {\displaystyle \frac{{\displaystyle m\omega _{0}^{2} X_{0}^{2} }}{{\displaystyle 2}}}e^{ - 2\beta t}{\displaystyle \left[ {\displaystyle 1 + \cos \left( {\displaystyle 2\omega t + 2\varphi _{0} + \vartheta } \right) \cdot \cos \left( {\displaystyle - \vartheta } \right)} \right]}$

Энергия механической колебательной системы совершает колебания с удвоенной частотой и затухает со временем быстрее, чем скорость или координата (коэффициент затухания для энергии равен 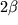$2\beta$ ).

Добротность - величина, характеризующая качество колебательной системы, равная отношению энергии, запасенной в системе к энергии, теряемой за один период колебаний.

$Q = 2\pi {\displaystyle \frac{{\displaystyle E}}{{\displaystyle {\displaystyle \left| {\displaystyle \Delta E_{T} } \right|}}}}.$

Чем больше добротность, тем "лучше" система "приспособлена" для совершения колебаний, тем меньше энергии теряется за один цикл колебаний.

Энергия убывает по закону $E\left( {\displaystyle t} \right) = E_{0} \exp \left( {\displaystyle - 2\beta t} \right).$ Подставим выражение энергии и выражение для изменения энергии за один период колебаний

$\left| {\displaystyle \Delta E_{T} } \right|} = E_{0} {\displaystyle \left[ {\displaystyle \exp \left( {\displaystyle - 2\beta t} \right) - \exp \left( {\displaystyle - 2\beta \left( {\displaystyle t + T} \right)} \right)} \right]}\quad или \quad {\displaystyle \left| {\displaystyle \Delta E_{T} } \right|} = E_{0} \exp \left( {\displaystyle - 2\beta t} \right){\displaystyle \left[ {\displaystyle 1 - \exp \left( {\displaystyle - 2\beta T} \right)} \right]$

в выражение для добротности

$Q = 2\pi {\displaystyle \frac{{\displaystyle E_{0} \exp \left( {\displaystyle - 2\beta t} \right)}}{{\displaystyle E_{0} \exp \left( {\displaystyle - 2\beta t} \right){\displaystyle \left[ {\displaystyle 1 - \exp \left( {\displaystyle - 2\beta T} \right)} \right]}}}}$

Преобразует полученное выражение к виду

$Q = 2\pi {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle 1 - \exp \left( {\displaystyle - 2\beta T} \right)}}}$

Поскольку в подавляющем большинстве случаев мы имеем дело с малым затуханием (выражение 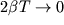$2\beta T \to 0$ ), то знаменатель последнего выражения можно разложить в ряд. Тогда

$Q \approx {\displaystyle \frac{{\displaystyle 2\pi }}{{\displaystyle 1 - \left( {\displaystyle 1 - 2\beta T} \right)}}} = {\displaystyle \frac{{\displaystyle \pi }}{{\displaystyle \beta T}}}\quad или \quad Q \approx {\displaystyle \frac{{\displaystyle \pi }}{{\displaystyle \chi }}} = {\displaystyle \frac{{\displaystyle \omega }}{{\displaystyle 2\beta }}}.$

Замечание. Часто добротность определяют, как отношение резонансной амплитуды колебаний (т.е. $X_{0} \left( {\displaystyle \Omega _{p} } \right)$ ) к статическому отклонению (т.е. отклонению под действием постоянной силы $X_{0} \left( {\displaystyle 0} \right)$ ). Т.е. $Q = {\displaystyle \frac{{\displaystyle X_{0} \left( {\displaystyle \Omega _{p} } \right)}}{{\displaystyle X_{0} \left( {\displaystyle 0} \right)}}}.$ Что, впрочем, после всех вычислений, приводит к тому же результату

$Q = {\displaystyle \frac{{\displaystyle \pi }}{{\displaystyle \chi }}} = {\displaystyle \frac{{\displaystyle \omega }}{{\displaystyle 2\beta }}}.$

Часть 2. Колебания в системе с двумя степенями свободы

4. Свободные колебания связанных маятников

Реальная физическая система при учете всех возможных в ней типов движения обладает практически бесконечным числом степеней свободы. Но в абстрактной модели необходимо учитывать лишь тот масштаб времени и амплитуды смещений, который можно (и нужно) зарегистрировать. Даже после жестокого отбора остается очень немного задач, в которых систему можно описать при помощи одной переменной. Значительная часть физических процессов описывается только с учетом бесконечного числа степеней свободы (распределенные системы) или многих степеней свободы (многоатомные молекулы, кристаллические решетки).

В системе со многими степенями свободы ее различные фрагменты при колебаниях меняют свою амплитуду колебаний, что позволяет говорить о том, что происходит изменение запаса энергии (усредненного за некоторый промежуток времени) данного фрагмента. Это говорит о то, что в системе происходит периодическое перераспределение энергии между фрагментами системы. [Г.Л. Деденко и др., 1991]

Лишь в двух специальных случаях в системе наблюдаются стационарные колебания:

При фиксированных положениях всех элементов, кроме одного. В этом случае система искусственно переводится в режим колебаний с одной степенью свободы. Частота такого типа колебаний называется парциальной частотой, а "остаток колебательной системы" - парциальной колебательной системой. Число парциальных частот равно числу степеней свободы.
Удачным подбором начальных условий иногда удается возбудить колебания с постоянной во времени амплитудой всех элементов. Такие колебания называются собственными или нормальными колебаниями. Их число также совпадает с числом степеней свободы системы.

Назад| Вперед

П.В.Кузьмин

Написать комментарий