Научная Сеть >> Колебания. Краткий конспект лекций.

Наука >> Физика >> Общая физика >> Колебания и волны >> Электрические колебания | Курсы лекций

Написать комментарий

Добавить новое сообщение

См. также

Б.А. Бахметев дипломат, политик, мыслитель

Колебания. Краткий конспект лекций.

П.В. Кузьмин (Костромская Государственная Сельскохозяйственная Академия)
Издательство КГСХА, 2002 г.

Содержание

Раскроем скобки и перегруппируем слагаемые

$\left\{\displaystyle {\displaystyle \begin{array}{l} {{\displaystyle \frac{{\displaystyle d^{2}\varphi _{1} }}{{\displaystyle dt^{2}}}} + {\displaystyle \frac{{\displaystyle m_{1} gL_{1} + ka^{2}}}{{\displaystyle m_{1} L_{1}^{2} }}}\varphi _{1} - {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{1} L_{1}^{2} }}}\varphi _{2} = {\displaystyle \frac{{\displaystyle M_{0} }}{{\displaystyle m_{1} L_{1}^{2} }}}\cos \left( {\displaystyle \Omega t + \theta } \right)} \\ {{\displaystyle \frac{{\displaystyle d^{2}\varphi _{2} }}{{\displaystyle dt^{2}}}} + {\displaystyle \frac{{\displaystyle m_{2} gL_{2} + ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}\varphi _{2} - {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}\varphi _{1} = 0} \\ \end{array}} \right.$

Окончательно

$\left\{\displaystyle {\displaystyle \begin{array}{l} {{\displaystyle \frac{{\displaystyle d^{2}\varphi _{1} }}{{\displaystyle dt^{2}}}} + \left( {{\displaystyle \frac{{\displaystyle g}}{{\displaystyle L_{1} }}} + {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{1} L_{1}^{2} }}}} \right)\varphi _{1} - {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{1} L_{1}^{2} }}}\varphi _{2} = {\displaystyle \frac{{\displaystyle M_{0} }}{{\displaystyle m_{1} L_{1}^{2} }}}\cos \left( {\displaystyle \Omega t + \theta } \right)} \\ {{\displaystyle \frac{{\displaystyle d^{2}\varphi _{2} }}{{\displaystyle dt^{2}}}} + \left( {{\displaystyle \frac{{\displaystyle g}}{{\displaystyle L_{2} }}} + {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}} \right)\varphi _{2} - {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}\varphi _{1} = 0} \\ \end{array}} \right.$

Полученная система - система дифференциальных уравнений вынужденных колебаний системы двух связанных маятников.

Рассмотрим установившиеся вынужденные колебания (т.е. считаем, что собственные колебания затухли, но силами сопротивления в системе можно пренебречь)

Будем искать решение в виде $\varphi _{1} (t) = C_{1} \cos (\Omega t + \theta ),\quad \varphi _{2} (t) = C_{2} \cos (\Omega t + \theta ).$

Используя выражения для парциальных частот, преобразуем:

$\left\{\displaystyle {\displaystyle \begin{array}{l} {\displaystyle - \Omega ^{2}C_{1} + \omega _{p1}^{2} C_{1} - {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{1} L_{1}^{2} }}}C_{2} = {\displaystyle \frac{{\displaystyle M_{0} }}{{\displaystyle m_{1} L_{1}^{2} }}}} \\ {\displaystyle - \Omega ^{2}C_{2} + \omega _{p2}^{2} C_{2} - {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}C_{1} = 0} \\ \end{array}} \right.}{\displaystyle \begin{array}{*{20}c} {\displaystyle \Rightarrow } \hfill & {{\displaystyle \left\{\displaystyle {\displaystyle \begin{array}{l} {\displaystyle \left( {\displaystyle \omega _{p1}^{2} - \Omega ^{2}} \right)C_{1} = {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{1} L_{1}^{2} }}}C_{2} + {\displaystyle \frac{{\displaystyle M_{0} }}{{\displaystyle m_{1} L_{1}^{2} }}}} \\ {\displaystyle \left( {\displaystyle \omega _{p2}^{2} - \Omega ^{2}} \right)C_{2} = {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}C_{1} } \\ \end{array}} \right.}} \hfill \\ \end{array}$

Далее выразим $C_{1}$ из второго выражения системы и подставим в первое.

$\left\{\displaystyle {\displaystyle \begin{array}{l} {{\displaystyle \frac{{\displaystyle \left( {\displaystyle \omega _{p1}^{2} - \Omega ^{2}} \right)\left( {\displaystyle \omega _{p2}^{2} - \Omega ^{2}} \right)}}{{\displaystyle {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}}}}C_{2} = {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{1} L_{1}^{2} }}}C_{2} + {\displaystyle \frac{{\displaystyle M_{0} }}{{\displaystyle m_{1} L_{1}^{2} }}}} \\ {{\displaystyle \frac{{\displaystyle \left( {\displaystyle \omega _{p2}^{2} - \Omega ^{2}} \right)}}{{\displaystyle {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}}}}}C_{2} = C_{1} } \\ \end{array}} \right.$

Окончательно найдем амплитуды вынужденных колебаний маятников

${\displaystyle \left\{\displaystyle {\displaystyle \begin{array}{l} {\displaystyle C_{2} = {\displaystyle \frac{{\displaystyle M_{0} }}{{\displaystyle m_{1} L_{1}^{2} }}} \cdot {\displaystyle \frac{{\displaystyle ka^{2}}}{{\displaystyle m_{2} L_{2}^{2} }}} \cdot {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \left( {\displaystyle \omega _{p1}^{2} - \Omega ^{2}} \right)\left( {\displaystyle \omega _{p2}^{2} - \Omega ^{2}} \right) - {\displaystyle \frac{{\displaystyle k^{2}a^{4}}}{{\displaystyle m_{1} L_{1}^{2} m_{2} L_{2}^{2} }}}}}}} \\ {\displaystyle C_{1} = {\displaystyle \frac{{\displaystyle M_{0} }}{{\displaystyle m_{1} L_{1}^{2} }}} \cdot {\displaystyle \frac{{\displaystyle \left( {\displaystyle \omega _{p2}^{2} - \Omega ^{2}} \right)}}{{\displaystyle \left( {\displaystyle \omega _{p1}^{2} - \Omega ^{2}} \right)\left( {\displaystyle \omega _{p2}^{2} - \Omega ^{2}} \right) - {\displaystyle \frac{{\displaystyle k^{2}a^{4}}}{{\displaystyle m_{1} L_{1}^{2} m_{2} L_{2}^{2} }}}}}}} \\ \end{array}} \right.}.$

Зависимость амплитуды колебания маятников от частоты (см. рис.5.1) резонансное возрастание амплитуды наблюдается вблизи обеих частот.

Рис. 5.1

Обратите внимание на подавление колебаний первого маятника (к которому приложена вынуждающая сила) на парциальной частоте второго маятника. Такое подавление вызвано компенсацией момента вынуждающей силы моментом силы, действующей со стороны второго маятника. Этот эффект применяется на практике в механических успокоителях колебаний.

Часть 3. Электромагнитные колебания

6. Свободные электромагнитные колебания

6.1.Квазистационарный электрический ток

При изучении переменных во времени токов и полей необходимо принять во внимание два фактора:

Конечную скорость распространения электромагнитных полей.
Порождение магнитного поля электрическим полем, изменяющимся во времени (речь идет о токе смещения).

При не очень большой частоте этими факторами можно пренебречь, т.е. можно считать, что электромагнитные поля распространяются в пространстве мгновенно, а токи смещения не существуют.

Токи и поля, удовлетворяющие этим условиям, называются квазистационарными. Выразим эти критерии математически.

Условие квазистационарности можно записать и в формулировке введения (стр. 4) [И.В. Савельев, 1982], но...

Если имеется периодический процесс, распространяющийся от источника с конечной скоростью c. То длина волны этого процесса равна $\lambda = cT.$

Пренебречь пространственным изменением некоторой величины, характеризующей процесс, можно только в том случае, если она рассматривается в областях, линейные размеры которых много меньше длины волны, т.е. $d \ll \lambda .$ Это и есть критерий пренебрежения конечной скоростью распространения возмущения.

Например, для технического тока частотой 50 Гц длина волны $\approx 6000$ км. Поэтому если нас интересуют вопросы, связанные с распределением тока по проводникам в пределах электростанции или даже города, то ток можно считать квазистационарным.

Если индукция электрического поля меняется по гармоническому закону с частотой $\Omega ,$ то амплитуда плотности тока смещения $j_{0см} = \Omega D_{0} = \Omega \varepsilon _{0} \varepsilon E_{0} .$ Плотность тока проводимости $j_{0} = \sigma E_{0} .$ Пренебречь эффектом тока смещения можно в том случае, если ${\displaystyle \frac{{\displaystyle j_{0см} }}{{\displaystyle j_{0} }}} = {\displaystyle \frac{{\displaystyle \Omega \varepsilon _{0} \varepsilon }}{{\displaystyle \sigma }}} \ll 1.$ Если подставить значения, то это можно сделать вплоть до частот порядка 10¹⁸ Гц (ультрафиолетовая часть спектра).

Необходимо помнить, что эта оценка приближенная, поскольку не учитывает инерционных свойств среды.

Однако для переменных электромагнитных полей в отсутствие токов проводимости учет токов смещения как источника магнитного поля является необходимым для всех частот.[А.Н. Матвеев, 1983]

6.2. Свободные электромагнитные колебания в идеальном электрическом контуре

Идеальным электрическим контуром называется контур с бесконечно-малым активным сопротивлением.

Т.к. активное сопротивление мало, то его можно принять равным нулю. Следовательно, в таком контуре не будет потерь энергии при колебаниях. (Схема 1.)

Схема 1

Запишем для квазистационарного тока в контуре уравнение, составленное по закону Ома.

$U_{L} + U_{C} = 0,$

(35)

где $U_{L} = L{\displaystyle \frac{{\displaystyle dI}}{{\displaystyle dt}}}$ - напряжение на катушке, связанное с явлением самоиндукции и $U_{C} = {\displaystyle \frac{{\displaystyle q}}{{\displaystyle C}}}$ - напряжение на конденсаторе. Правая часть уравнения равна нулю, т.к. источников в контуре нет. Тогда выражение (35) примет вид

$L{\displaystyle \frac{{\displaystyle dI}}{{\displaystyle dt}}} + {\displaystyle \frac{{\displaystyle q}}{{\displaystyle C}}} = 0.$

(36)

Учитывая, что $I = {\displaystyle \frac{{\displaystyle dq}}{{\displaystyle dt}}},$ уравнение (36) можно привести к виду

$L{\displaystyle \frac{{\displaystyle d^{2}q}}{{\displaystyle dt^{2}}}} + {\displaystyle \frac{{\displaystyle q}}{{\displaystyle C}}} = 0.$

Введем обозначение 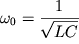$\omega _{0} = {\displaystyle \frac{{\displaystyle 1}}{{\displaystyle \sqrt {\displaystyle LC} }}}$ (частота собственных незатухающих колебаний или собственная частота), окончательно получим

${\displaystyle \frac{{\displaystyle d^{2}q}}{{\displaystyle dt^{2}}}} + \omega _{0}^{2} q = 0.$

(37)

Сравните с выражением (2). Выражение (37) - это дифференциальное уравнение свободных гармонических незатухающих колебаний электрическом контуре.

(Аналогия между механическими и электромагнитными колебаниями: координата - заряд, скорость - сила тока.)

Из п. 1.1 известно, что решением этого уравнения является функция (если подходить формально, то в выражении (5) координату необходимо поменять на заряд, а скорость на силу тока)

$q(t) = q_{0} \cos (\omega _{0} t) + {\displaystyle \frac{{\displaystyle i_{0} }}{{\displaystyle \omega _{0} }}}\sin (\omega _{0} t) \quad ,$

(38)

Где $q_{0} = q\left( {\displaystyle 0} \right),\quad i_{0} = {\displaystyle \frac{{\displaystyle dq\left( {\displaystyle 0} \right)}}{{\displaystyle dt}}}$ - заряд на конденсаторе и сила тока в контуре в момент времени равный нулю.

Выражение (38) можно привести к виду

$q(t) = Q\cos (\omega _{0} t + \varphi _{0} ),$

(39)

где амплитуда и начальная фаза: $Q = \sqrt {\displaystyle q_{0}^{2} + {\displaystyle \frac{{\displaystyle i_{0}^{2} }}{{\displaystyle \omega _{0}^{2} }}}} ,\quad \varphi _{0} = arctg\left( {\displaystyle - {\displaystyle \frac{{\displaystyle i_{0} }}{{\displaystyle \omega _{0} q_{0} }}}} \right).$

Т.о. амплитуда и начальная фаза находятся из начальных условий для заряда и силы тока, а частота собственных незатухающих колебаний - через параметры колебательной системы (индуктивность и электроемкость).

Назад| Вперед

П.В.Кузьмин

Написать комментарий