Есть бесконечная цилиндрическая "половинчатая" поверхность (то есть в сечении, перпендикулярном оси, получается не окружность, а полуокружность) радиуса а, заряженная равномерно с погонной плотностью заряда k. Требуется определить потенциал в точке, находящейся в той плоскости, которая содержит диаметр поверхности. Точка на расстоянии l от оси.
Мне кажется, что потенциал во всей этой плоскости будет постоянен. Я прав? Если нет, то, плиз, подскажите, как решать
Полная версия этой страницы: Задача по электростатике
В принципе все задачки электростатики на вычисление потенциала с известным расположением зарядов решаются одной формулой
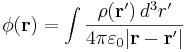
Аналогичная формула для электрического поля
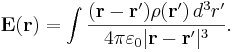
Весь вопрос только в том, сможете ли Вы вычислить интеграл.
Я не уверен, что правильно понял описанную Вами геометрию, было бы неплохо, если бы Вы нарисовали картинку. Если же я все понял правильно, то у меня сильное подозрение, что нужен Вам не потенциал, а напряженность поля. Насколько я понимаю, в этой задаче с потенциалом проблемы: во-первых, он не может быть нормирован на нуль на бесконечности (а как тогда нормировать?), во-вторых, интеграл для потенциала не считается в элементарных функциях. В то же время интеграл для напряженности вычисляется, хоть и не совсем просто (а нормировать ее вовсе не надо).
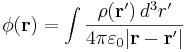
Аналогичная формула для электрического поля
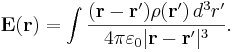
Весь вопрос только в том, сможете ли Вы вычислить интеграл.
Я не уверен, что правильно понял описанную Вами геометрию, было бы неплохо, если бы Вы нарисовали картинку. Если же я все понял правильно, то у меня сильное подозрение, что нужен Вам не потенциал, а напряженность поля. Насколько я понимаю, в этой задаче с потенциалом проблемы: во-первых, он не может быть нормирован на нуль на бесконечности (а как тогда нормировать?), во-вторых, интеграл для потенциала не считается в элементарных функциях. В то же время интеграл для напряженности вычисляется, хоть и не совсем просто (а нормировать ее вовсе не надо).
Здесь можно обойтись и без интегралов, воспользовавшись известным фокусом, основанным на принципе суперпозиции.
Задача эффективно двумерная. Введем плоскость) перпендикулярно оси цилиндра. Пусть одна половинка цилиндра (будем считать, что она лежит в верхней полуплоскости) создает потенциал
перпендикулярно оси цилиндра. Пусть одна половинка цилиндра (будем считать, что она лежит в верхней полуплоскости) создает потенциал ) . Тогда другая половинка (нижняя) создавала бы потенциал
. Тогда другая половинка (нижняя) создавала бы потенциал ) - по симметрии задачи. Вместе они бы создавали потенциал
- по симметрии задачи. Вместе они бы создавали потенциал  %2b\phi(x,-y) = \phi^{cil}(x,y)) , т.е. потенциал полного цилиндра. Этот потенциал элементарно считается по теореме Остроградского-Гаусса.
, т.е. потенциал полного цилиндра. Этот потенциал элементарно считается по теореме Остроградского-Гаусса.
Нам надо знать потенциал только на оси x, т.е.) :
:  %2b \phi(x,0) = \phi^{cil}(x,0)) . Все.
. Все.
И да, на бесконечности проблема с потенциалом, конечно, есть. Но в таких задачах на это обычно не обращают внимания. Благо с напряженностью все в поряде.
Задача эффективно двумерная. Введем плоскость
Нам надо знать потенциал только на оси x, т.е.
И да, на бесконечности проблема с потенциалом, конечно, есть. Но в таких задачах на это обычно не обращают внимания. Благо с напряженностью все в поряде.
ignit0r, так Вы хотите сказать, что я неправильно понял геометрию? Мне казалось, что полутруба симметрична относительно отражения в плоскости, в которой надо найти потенциал. А если все так, как Вы говорите, тогда, конечно, задача совсем простая.
ignit0r, думаю, Вы правы. К тому же не дан радиус трубы, а при моем (ошибочном) понимании геометрии он нужен.
Для Перегудова: рассматриваемая плоскость содержит края поверхности и параллельна оси цилиндра. По поводу нормировки: делаем как для заряженной плоскости -- на поверхности потенциал ноль, а на бесконечности бесконечность (а что такого? -- ведь заряда тоже бесконечно много). Да, Вы правы, интеграл для потенциала сводится к эллиптическому, поэтому я не смог его в человеческом виде выписать. Напряженность считать не пробовал, надо посмотреть.
Для ignit0r: я так и делал, и если принять, что на поверхности полутрубы потенциал ноль, то при l<R (R -- радиус цилиндра) потенциал в нашей плоскости тоже нулевой, а в общем случае (когда на поверхности задаем не нулевой потенциал) просто константа. Об этом я писал в начальном посте (правда, не уточнив, что я говорю про l<R). И меня это засмущало, так как получается, что это l вообще не нужно (у меня в задаче по условию требуется определить потенциал в диаметральной плоскоти при l<R -- я это в формулировке не указал, но это не важно). Конечно, принцип суперпозиции никто не отменял, но точно все правильно?
Для ignit0r: я так и делал, и если принять, что на поверхности полутрубы потенциал ноль, то при l<R (R -- радиус цилиндра) потенциал в нашей плоскости тоже нулевой, а в общем случае (когда на поверхности задаем не нулевой потенциал) просто константа. Об этом я писал в начальном посте (правда, не уточнив, что я говорю про l<R). И меня это засмущало, так как получается, что это l вообще не нужно (у меня в задаче по условию требуется определить потенциал в диаметральной плоскоти при l<R -- я это в формулировке не указал, но это не важно). Конечно, принцип суперпозиции никто не отменял, но точно все правильно?
рассматриваемая плоскость содержит края поверхности и перпендикулярна оси цилиндра
Это как? Видимо, рисунок таки нужен.
Об этом я писал в начальном посте (правда, не уточнив, что я говорю про l<R). И меня это засмущало, так как получается, что это l вообще не нужно (у меня в задаче по условию требуется определить потенциал в диаметральной плоскоти при l<R -- я это в формулировке не указал, но это не важно)
Да, константа внутри радиуса. А снаружи растет логарифмически.
Простите, это я уже записался: конечно, плоскость содержит края и параллельна оси цилиндра.
Не знаю, нужно ли мое мнение, но я полностью согласен с ignit0r'ом.
Для просмотра полной версии этой страницы, пожалуйста, пройдите по ссылке.
