Астронет > Колебания и волны

Астронет: Научная Сеть/НС Колебания и волны
http://variable-stars.ru/db/msg/1175791/page38.html

Колебания и волны. Лекции.

В.А.Алешкевич, Л.Г.Деденко, В.А.Караваев (Физический факультет МГУ)
Издательство Физического факультета МГУ, 2001 г. Содержание

В качестве примера выполним некоторые оценки, иллюстрирующие количественные характеристики распространения звуковой волны в воде, где $D = 300 (Па с)^{-1}.$ При частоте ультразвука $\nu = 1 МГц$ расстояние $\ell _{з} = 50 м,$ и условие ${\displaystyle \rm Re} \gt 10$ выполняется, согласно (6.58), для волн с амплитудой звукового давления $(\delta p)_{0} \gt 3 \cdot 10^{4}Па,$ или интенсивностью

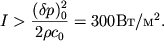$I \gt {\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0}^{2} }}{\displaystyle {\displaystyle 2\rho c_{0} }}} = 300Вт/м^{2}.$

(6.59)

Соответствующий уровень звукового давления $L_{p} \gt 180 дБ.$ Для волн с такими интенсивностями $\ell _{нл} \lt \ell _{з} / 10 = 5 м,$ поэтому уже на первых метрах своего распространения ультразвуковая волна будет превращаться в пилообразную, и затем при $x \gt \ell _{нл}$ начнется ее нелинейное затухание.

Как показывает анализ формулы (6.54) с учетом построения положения ударного фронта, изображенного на рис. 6.11, амплитуда пилообразной волны при ${\displaystyle \rm Re} \gg 1$ убывает с пройденным расстоянием $x$ по закону

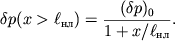$\delta p(x \gt \ell _{нл} ) = {\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0} }}{\displaystyle {\displaystyle 1 + x / \ell _{нл} }}}.$

(6.60)

С помощью этой формулы сразу можно сделать важный вывод о том, что величина $\delta p$ не может превзойти некоторое предельное значение, как бы мы ни увеличивали амплитуду гармонической волны $(\delta p)_{0}.$ Действительно, при увеличении $(\delta p)_{0}$ величина $\ell _{нл} \sim 1 / (\delta p)_{0}$ уменьшается, и $\delta p$ стремится к $\delta p_{\max }.$ Величина $\delta p_{\max }$ может быть корректно подсчитана при одновременном учете линейного поглощения и нелинейного затухания (это выходит за рамки нашего курса) и оказывается равной

$\delta p_{\max } = {\displaystyle \frac{\displaystyle {\displaystyle 4\nu }}{\displaystyle {\displaystyle D}}}e^{ - x / \ell _{з} }.$

(6.61)

Оценим максимальное значение интенсивности $I_{max},$ которая может быть передана в воде ультразвуковым лучом с частотой $\nu = 1 МГц$ на расстояние $x = 2\ell _{з} = 100 м$ :

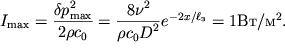$I_{\max } = {\displaystyle \frac{\displaystyle {\displaystyle \delta p_{\max }^{2} }}{\displaystyle {\displaystyle 2\rho c_{0} }}} = {\displaystyle \frac{\displaystyle {\displaystyle 8\nu ^{2}}}{\displaystyle {\displaystyle \rho c_{0} D^{2}}}}e^{ - 2x / \ell _{з} } = 1 Вт/м^{2}.$

(6.62)

Таким образом, в условиях, наилучших для возбуждения мощных ультразвуковых волн в воде, на расстояние $x = 100 м$ через площадь сечения 1 м² можно передать энергию, достаточную лишь для свечения лампочки от карманного фонарика. Это ни в какое сравнение не идет с той энергией, которую посылают ультразвуковые пушки, используемые героями научно-фантастического романа Г. Адамова "Тайна двух океанов", где ультразвуковым лучом якобы повреждают корабли и ракеты.

В связи с вышеизложенным возникает естественный вопрос - а как же объяснить разрушающее действие взрывных ударных волн на большом расстоянии от места взрыва? Ответ на этот вопрос кроется в том, что взрывная ударная волна представляет собой одиночный импульс, и его амплитуда $\delta p$ убывает с расстоянием x более медленно, чем у гармонической волны:

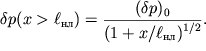$\delta p(x \gt \ell _{нл} ) = {\displaystyle \frac{\displaystyle {\displaystyle (\delta p)_{0} }}{\displaystyle {\displaystyle (1 + x / \ell _{нл} )^{1 / 2}}}}.$

(6.63)

При возрастании в эпицентре взрыва амплитуды импульса $(\delta p)_{0}$ будет неограниченно увеличиваться и величина $\delta p,$ которая при большой мощности заряда окажется достаточной для разрушения препятствия.

Надо отметить, что тем не менее нелинейное затухание не ограничивает широкое применение ультразвука в лабораторных условиях, поскольку $\ell _{нл}$ обычно сравнима с размерами лабораторных акустических систем или превосходит их.

До сих пор мы говорили о распространении только одной волны. Однако если распространяются, например, две волны с частотами $\omega _{1}$ и $\omega _{2},$ то нелинейное взаимодействие между ними приводит к появлению волн с другими частотами. Среди них волны с кратными частотами $n_{1} \omega _{1}$ и $n_{2} \omega _{2}$ (гармоники) и волны с комбинационными частотами $n_{1} \omega _{1} \pm n_{2} \omega _{2}$ ( $n_{1}$ и $n_{2}$ - целые числа). В акустике, где дисперсия отсутствует, все эти волны движутся с одинаковой скоростью, поэтому они могут эффективно взаимодействовать между собой, проходя большие расстояния.

Генерация гармоник и волн с комбинационными частотами имеет многочисленные применения. Проиллюстрируем сказанное на двух примерах.

1. При изучении упругих и прочностных свойств твердых материалов их обычно подвергают большим нагрузкам с помощью специальных прессов, развивающих давления, близкие к пределам прочности этих материалов или превосходящие их, т.е. десятки тысяч атмосфер. Вместо этой громоздкой и дорогостоящей аппаратуры используют методы нелинейной акустики. Для этого к одному торцу образца исследуемого материала приклеивают пьезоэлектрический излучатель мощной акустической волны частоты $\omega.$ На другом конце образца помещают такой же пьезоэлектрический преобразователь (приемник звука), на выходе которого регистрируют и затем обрабатывают электрический сигнал. Последний представляет собой суперпозицию колебаний на частотах $\omega, 2\omega, 3\omega$ и т.д. Говорят, что сигнал состоит из основной, второй, третьей и т.д. гармоник. Сигнал на основной частоте несет информацию о линейном модуле Юнга, так как согласно закону Гука деформации пропорциональны приложенным напряжениям. В области больших напряжений вследствие пластичности и текучести материала связь деформаций и напряжений описывают с использованием нелинейных модулей. Информацию о таких модулях несет уже амплитуда сигнала с частотой $2\omega$ (вторая гармоника), и т.д.

2. Другим ярким примером использования методов нелинейной акустики является генерация в воде узконаправленных пучков акустических волн с длиной $\lambda .$ Это осуществляется с помощью так называемых параметрических антенн. При знакомстве с явлением дифракции волн мы отмечали, что угловая расходимость $\vartheta$ звукового пучка тем меньше, чем больше размер $\ell$ передающего излучателя (антенны). Проблему изготовления огромных излучающих антенн с размерами в десятки метров можно обойти, используя нелинейное взаимодействие в воде двух параллельно распространяющихся мощных звуковых волн с близкими частотами $\omega _{1}$ и $\omega _{2}.$ Эти волны излучаются горизонтально погруженным в воду одним пьезоизлучателем размером $\ell \sim 10 см.$ Обе волны до их затухания пройдут расстояние $L\sim 10^{3} м.$ В этой протяженной области рождается волна низкой (разностной) частоты $\omega = \omega _{2} - \omega _{1},$ которая затухает гораздо слабее и может пройти очень большие расстояния. Таким образом, вытянутый объем воды с малым поперечным размером $\ell$ и большим продольным размером $L$ представляет собой гигантскую естественную антенну, излучающую звуковой пучок разностной частоты вдоль самой вытянутой антенны. Однако, расходимость $\vartheta$ этого пучка уже будет задаваться выражением

$\vartheta = \lambda / L.$

(6.64)

При частоте $\nu = \omega / 2\pi \sim 1 кГц,\; \lambda \sim 1 м$ и при $L\sim 10^{3} м$ получаем $\vartheta \sim 3\cdot 10^{ - 2} рад = 1,8^{ \circ }.$ Такая чрезвычайно малая расходимость пучка разностной частоты позволяет с большой точностью проводить морские исследования: изучать рельеф дна, заниматься археологическими изысканиями в придонных слоях грунта, в заиленных озерах, обнаруживать скопления рыбы у поверхности и дна моря, на мелководье - там, где обычные гидролокаторы неэффективны, и т.д.

Назад| Вперед