 |
Астронет: А. В. Тунцов/Физический факультет МГУ Энтропия большого канонического ансамбля в расширяющейся Вселенной http://www.variable-stars.ru/db/msg/1176959/node4.html |
<< 2. Энтропия | Оглавление | 4. Заключение >>
3. Модельный конфигурационный интеграл
Для вычисления конфигурационного интеграла воспользуемя стандартным Ван дер Ваальсовским способом. Хотя применимость его здесь вряд ли обоснованна в виду дальнодействия затронутых сил, в оправдание можно привести лишь отсутствие других способов.
Итак, замечая, что 
, ибо поведение кинетической и
потенциальной энергии, по-видимому, должно быть согласованно (см. далее),
и считая, что потенциал имеет форму ямы глубиной 
и размером 
(
, - порядка размеров галактики), а также
вычитая из него среднюю энергию, равную
(
- коэффициент
порядка еденицы, зависящий от формы объема и равный для шара
), имеем следующие выражения:
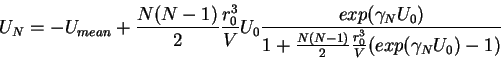
откуда
 |
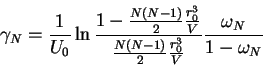(9) |
 |
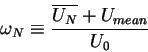(10) |
:
 |
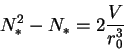(11) |
видно, что необходимо выполнение
следующего условия: 
при 
, 
при 
.
Отсюда, учитывая знак 
еще одно условие на применимость написанных
формул:
Теперь, после некоторых перобразований, можно получить для энтропии:
Уже отсюда видно, что квадратичная зависимость 
от 
оставляет лишь присущую идеальному газу часть этого выражения, но это
говорит скорее о слабости модели, чем о невозможности такого поведения.
Тем не менее, мы предположим, что поведение также линейно с
ростом числа частиц. В качестве обоснования можно сослаться на работы
(Layzer, 1963; Irvine, 1965), показавших, что в среднем во Вселенной
корреляционная часть энергии и кинетическая энергия ведут себя согласованно
(стремясь в итоге к вириализованному состоянию). Совместно с условиями на
, 
и выражением для , это дает:
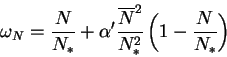
где
. При этом
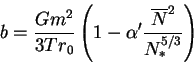
Это выражение, с учетом всех наложенных условий, уже может иметь
отношение к реальности и дает отличные от нуля слагаемые, отвечающие за
изменение энтропии взаимодействием. Его уже можно исполдьзовать - по крайней
мере, для достаточно разреженных систем (а для типичных скоплений выполнено,
что
) - для отдания предпочтения тому или другому
варианту распределения 
.
Для выражения (12) с учетом условий (5) можно решить
и более общую задачу с любыми разумныни - найти экстремальное
распределение , доставляющее максимум энтропии. Приравняв вариационную
производную нулю, получим:
 |
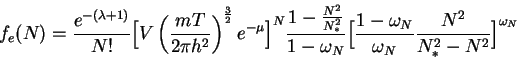(13) |
и 
определяются из условий
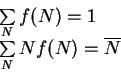
Эти формулы, тем не менее, будучи применены к конкретным ситуациям, несмотря на кажущееся значительное отличие, дают распределения, близкие к Пуассоновому. Дальнейшая работа необходима для более тщательного исследования этого вопроса.
<< 2. Энтропия | Оглавление | 4. Заключение >>