Астронет > Сферическая астрономия

Астронет: В. Е. Жаров/ГАИШ Сферическая астрономия
http://www.astronet.ru/db/msg/1190817/node87.html

<< A.3 Декартовы прямоугольные и | Оглавление | A.5 Криволинейные координаты >>

A.4 Элементы дифференциального и интегрального исчисления

Дифференциал функции $y=f(x)$ в точке $x$ , если он существует, равен:

$\displaystyle dy = \frac{dy}{dx}dx=f'(x)dx,$

$f'(x)=dy/dx$ -- производная функции.

Дифференциал функции $y=f(x_1,x_2,\ldots,x_n)$ , если он существует, равен:

$\displaystyle dy = \frac{\partial{f}}{\partial{x}_1}dx_1+\frac{\partial{f}}{\partial{x}_2}dx_2+\ldots+ \frac{\partial{f}}{\partial{x}_n}dx_n,$

причем частные производные $\frac{\partial{f}}{dx_1},\ldots,\frac{\partial{f}}{dx_n}$ вычисляются в рассматриваемой точке.

Если $f(x)$ -- действительная функция, имеющая в интервале $a\leq x \lt b$ $n$ -ую производную $f^{(n)}$ , то

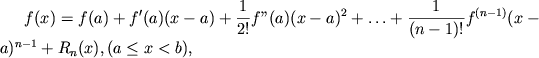
$$\displaystyle f(x)=f(a)+f'(a)(x-a)+\frac{1}{2!}f$

где $R_n(x)$ называется остаточным членом.

Градиентом скалярной функции $F({\mathbf{r}})=F(x,y,z)$ называется векторная функция, определяемая формулой:

$\displaystyle \textrm{grad}\ F({\mathbf{r}})$	$\displaystyle = \frac{\partial{F}}{\partial{x}}{\mathbf{i}} + \frac{\partial{F}}{\partial{y}}{\mathbf{j}} + \frac{\partial{F}}{\partial{z}}{\mathbf{k}}$	$\displaystyle \textrm{в декартовых координатах},$
$\displaystyle \textrm{grad}\ F({\mathbf{r}})$	$\displaystyle = \frac{\partial{F}}{\partial{r}}{\mathbf{i}}_r + \frac{1}{r}\frac{\partial{F}}{\partial{\theta}}{\mathbf{i}}_\theta + \frac{1}{r\sin\theta}\frac{\partial{F}}{\partial{\lambda}}{\mathbf{i}}_\lambda$	$\displaystyle \textrm{в сферических координатах}.$

Полный дифференциал $dF$ скалярной функции $F({\mathbf{r}})=F(x,y,z)$ , соответствующий перемещению точки на $d{\mathbf{r}} = dx\,{\mathbf{i}} + dy\,{\mathbf{j}} + dz\,{\mathbf{k}}$ равен:

$\displaystyle dF({\mathbf{r}}) = \frac{\partial{F}}{\partial{x}}dx + \frac{\partial{F}}{\partial{y}}dy + \frac{\partial{F}}{\partial{z}}dx = d{\mathbf{r}}\cdot \textrm{grad}\ F({\mathbf{r}}).$

Дифференциал $d{\mathbf{r}}$ радиус-вектора ${\mathbf{r}}$ вдоль кривой $C$ , описываемой уравнением

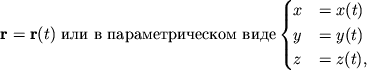
$\begin{displaymath} {\mathbf{r}}={\mathbf{r}}(t)\ \textrm{или в параметрическом виде} \begin{cases} x &=x(t) \\ y &=y(t) \\ z &=z(t), \end{cases}\end{displaymath}$

определяется в каждой точке ${\mathbf{r}}=\Bigl(x(t),y(t),z(t)\Bigr)$ кривой формулой:

$\displaystyle d{\mathbf{r}} = dx\,{\mathbf{i}} + dy\,{\mathbf{j}} + dz\,{\mathbf{k}} =\Bigl( \frac{dx}{dt}{\mathbf{i}} + \frac{dy}{dt}{\mathbf{j}} + \frac{dz}{dt}{\mathbf{k}}\Bigr)dt.$

Вектор $d{\mathbf{r}}$ направлен по касательной к кривой $C$ в точке с радиус-вектором ${\mathbf{r}}$ .

Квадрат элемента длины равен

$\displaystyle ds^2$	$\displaystyle = dx^2+dy^2+dz^2$	$\displaystyle \textrm{в декартовых координатах},$
$\displaystyle ds^2$	$\displaystyle = dr^2+r^2d\theta^2+r^2\sin^2\theta\, d\lambda^2$	$\displaystyle \textrm{в сферических координатах}.$

Преобразование дифференциалов из сферической в декартову систему координат имеет вид:

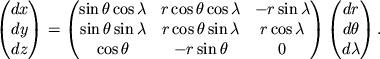
$\displaystyle \begin{pmatrix} dx \\ dy \\ dz \end{pmatrix} = \begin{pmatrix} \sin\theta\cos\lambda & r\cos\theta\cos\lambda & -r\sin\lambda\\ \sin\theta\sin\lambda & r\cos\theta\sin\lambda & r\cos\lambda\\ \cos\theta & -r\sin\theta & 0 \end{pmatrix}\begin{pmatrix} dr \\ d\theta \\ d\lambda \end{pmatrix}.$

<< A.3 Декартовы прямоугольные и | Оглавление | A.5 Криволинейные координаты >>