Астронет > Размерности и подобие астрофизических величин

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Размерности и подобие астрофизических величин << § 5.1 Пульсация переменных звезд | Оглавление | § 5.3 Турбулентность и конвекция >>

§ 5.2 Вращение и магнитные поля звезд

Наблюдения показывают, что звезды вращаются и что на их поверхности имеются магнитные поля, иногда очень сильные. Очевидно, что вращаются и внутренние части звезды и что там тоже есть магнитные поля, однако никаких сведений о характере вращения центральных частей звезд и о напряженностях магнитных полей внутри них у нас нет. Поэтому при исследовании структуры вращающихся и намагниченных звезд приходится делать произвольные допущения. Этим проблемам посвящено много работ, и в нашу задачу не входит их обзор. В частности, интерес к вращению и магнитным полям звезд очень возрос после открытия пульсаров - вращающихся намагниченных нейтронных звезд.

Мы ограничимся некоторыми обсуждениями методов теории анализа размерностей применительно к этой проблеме, тем более оправданного, что трудно составить полную, адекватную явлениям систему уравнений, а еще труднее найти решение подобных уравнений.

Разумеется, использование только метода теории размерностей для анализа соотношений между определяющими параметрами без решения соответствующих систем уравнений существенно ограничивает рассмотрение проблемы. Например, мы ничего не сможем сказать о распределении угловых скоростей вращения или магнитных полей в недрах звезды. Но, с другой стороны, получаемые результаты не зависят от этих распределений, которые до сих пор нельзя оценить хотя бы сколько-нибудь уверенно.

Рассмотрим теперь подробно набор определяющих параметров, которые могут характеризовать вращение и магнитные поля звезд. Вращение характеризуется угловой скоростью Ω;;; с размерностью [Ω;;;] = сек^-1. В реальных звездах величина Ω;;; меняется в очень широких пределах - от Ω;;; ≈ 200 сек^-1 у пульсара Крабовидной туманности до Ω;;; ≈ 2,7 ⋅ 10^-6 сек^-1 у Солнца и, вероятно, еще много меньше у звезд красных гигантов. Пока не ясно, насколько однородно (твердотельно) вращение звезды. Хорошо известно, что вращение поверхностных слоев Солнца неоднородно, экваториальные области вращаются с большей угловой скоростью, чем полярные, а верхние слои солнечной атмосферы вращаются быстрее более глубоких слоев. Неоднократно высказывалось предположение, что ядра звезд (например, конвективные ядра горячих звезд) вращаются быстрее остальной массы звезды. Мы будем считать вращение звезды твердотельным или по крайней мере будем рассматривать только среднюю угловую скорость Ω;;;. Второй существенный параметр вращающейся звезды - ее момент инерции

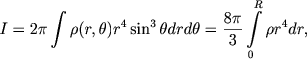
$I = 2\pi\int\rho(r,\theta)r^4\sin^3\theta drd\theta = \frac{8\pi}{3}\int\limits_0^R \rho r^4dr,$ (5.39)

где, по-прежнему, r есть расстояние до центра звезды, а θ - угол между радиусом-вектором и осью вращения (второе равенство - для случая, когда плотность зависит только от r). Величина момента инерции существенно зависит от распределения плотности внутри звезды, но для подобных звезд можно написать

$I = \zeta_n MR^2,$ (5.40)

где параметр ζ_n меньше единицы, а у звезд с большой концентрацией массы к центру (у красных гигантов) много меньше единицы.

Если в процессе эволюции звезды меняется ее момент инерции (изменяется как R, так и ζ_n, поскольку изменяется концентрация вещества к центру звезды), то меняется и угловая скорость в соответствии с законом сохранения момента вращения

$\mathfrak{M} = I\Omega = const.$ (5.41)

Правда, обсуждается вопрос и о потере момента вращения в процессе эволюции звезд. Такая потеря может быть вызвана уменьшением массы звезды из-за звездного ветра, или же момент вращения может отбираться от звезды при излучении ею магнитогидродинамических волн (см. ниже). Размерность момента вращения, который также является определяющим параметром, есть $\mathfrak {M}$ = г ⋅ см² ⋅ сек^-1. Еще один параметр - линейную скорость вращения - мы не будем считать определяющим. Линейную скорость вращения легко выразить через угловую скорость, а с другой стороны, в отличие от Ω;;; , I и $\mathfrak {M}$ , линейная скорость не определяет свойства вращения звезды в целом.

Однако есть еще одна величина с размерностью скорости, которая характеризует вращающиеся звезды. В уравнении гидростатического равновесия наряду с силой тяжести надо учесть и центробежную силу, которая, в отличие от первой, не является сферически-симметричной, но также лежит в меридиональных плоскостях. В результате поверхности равного уровня (одинаковой величины суммы гравитационного потенциала и потенциала центробежной силы) не совпадают со сферическими поверхностями одинаковой величины потока лучистой энергии. Этот эффект приводит к появлению циркуляции вещества звезды в меридиональных плоскостях. Циркуляционная скорость, обозначаемая в дальнейшем через v_c, много меньше как линейной скорости вращения, так и скорости конвективных движений. В конвективных зонах и ядрах подобной циркуляции нет.

Наконец, последний параметр, характеризующий вращающиеся звезды - коэффициент вязкости вещества, стремящийся выровнять неоднородность вращения, сделать его твердотельным. В конвективных зонах и ядрах существенна роль турбулентной вязкости и там вращение, по-видимому, быстро становится твердотельным. В области лучистого переноса энергии роль вязкости, по-видимому, много меньше, и там дольше может сохраняться неоднородность вращения. В качестве определяющего параметра выберем коэффициент динамической вязкости η, по порядку величины равный произведению плотности на длину свободного пробега и на скорость частиц, переносящих вращательный момент. Размерность этой величины [η] = г ⋅ см^-1 ⋅ сек^-1. Различные коэффициенты вязкости характеризуются соответствующей длиной свободного пробега и скоростью тех элементов, которые переносят количество движения. В турбулентной вязкости длина свободного пробега и скорость определяются размером и скоростью турбулентных вихрей.

В ионизованном газе вязкость определяется свободным пробегом и тепловой скоростью положительных ионов (протонов). Теория дает следующую формулу для коэффициента динамической вязкости ионизованной водородной плазмы:

$\eta \approx \frac{m_p^3}{e^4\Lambda}\left(\frac{\Re T}{\mu}\right)^{5/2} \approx 0,4 T_6^{5/2} \frac{\mbox{г}}{\mbox{см} \cdot \mbox{сек}},$ (5.42)

где Λ - кулоновский логарифм (Λ ≈ 10-100). В среде с большой плотностью излучения вязкость определяется длиной свободного пробега фотонов. Здесь имеет место динамический коэффициент лучистой вязкости

$\eta = \frac{c}{\varkappa}(1-\beta),$ (5.43)

где ϰ - обычный коэффициент непрозрачности.

Теперь обратимся к определяющим параметрам магнитного поля. Основной величиной является магнитная индукция В с размерностью

$\eta = \frac{c}{\varkappa}(1-\beta),$ (5.44)

На поверхности звезд значение величины В также варьируется в больших пределах - от величины порядка одного гаусса (общее магнитное поле Солнца) до нескольких тысяч гаусс у магнитных звезд, возможно, 10⁷ гаусс у белых карликов и, вероятно, 10¹⁰-10¹² гаусс - у пульсаров.

Структура магнитного поля внутри звезд остается неизвестной. Судя по тому, что на поверхности Солнца магнитное поле имеет сложную структуру, можно предполагать, что и внутри звезд имеются сложные магнитные конфигурации. Поскольку сейчас почти ничего нельзя сказать об этой структуре, часто предполагается, что внутри звезд (и, в частности, пульсаров) магнитное поле однородно, т. е. все магнитные силовые линии параллельны некоторой магнитной оси. Однородное внутри звезды магнитное поле создает вне его дипольное магнитное поле с дипольным моментом, равным

$\Xi = \frac{1}{2}B_0R^3,$ (5.45)

где B₀ - величина однородной магнитной индукции внутри звезды с радиусом R. Как известно, дипольное магнитное поле является потенциальным, т. е. вектор В вне звезды может быть выражен через магнитный потенциал Ψ , в данном случае равный

$\Psi = -\frac{\vec\Xi \vec r}{r^3},$ (5.46)

где $\vec\Xi$ - вектор, численная величина которого равна (5.45), направленный вдоль магнитной оси. Для поля имеем

$\vec B = grad\Psi.$ (5.47)

По-видимому, магнитная ось не совпадает с осью вращения звезды. У Солнца угол между обеими осями мал, но возможно, что у пульсаров магнитная ось даже перпендикулярна к оси вращения.

Часто вместо магнитной индукции В употребляют напряженность магнитного поля H. Вне звезды, где магнитная проницаемость почти точно равна единице, эти величины близки. Однако внутри звезды, где расположены источники магнитного поля, величины В и H различны и их разность определяется намагниченностью вещества звезды. Поскольку распределение источников магнитного поля внутри звезды неизвестно, мы по-прежнему будем характеризовать магнитное поле . внутри звезды только вектором $\vec B$ и магнитным моментом $\vec\Xi$ , размерность которого есть г^1/2 ⋅ см^5/2 ⋅ сек^-1.

Наряду с динамической вязкостью имеется и магнитная вязкость, определяющая затухание магнитного поля. Магнитная вязкость определяется электропроводностью плазмы, которая в случае полной ионизации равна

$\lambda = \frac{30}{\Lambda}\frac{m_p}{e^2}\left(\frac{\Re T}{\mu}\right)^{3/2}.$ (5.48)

Магнитная вязкость, аналогичная кинетической вязкости v=η/ρ, определяется соотношением

$\nu_m = \frac{c^2}{4\pi\lambda} \approx \frac{\Lambda}{80\pi}\frac{e^2c^2}{m_p}\left(\frac{\mu}{\Re T}\right)^{3/2}.$ (5.49)

Размерность этих величин такова:

$[\lambda] = \frac{1}{\mbox{сек}}, \quad [\nu_m] = \frac{\mbox{см}^2}{\mbox{сек}}.$ (5.50)

Рассматривая магнитные поля, следует учитывать величину плотности энергии магнитного поля

$\omega = \frac{B^2}{8\pi}$ (5.51)

и величину плотности магнитной силы

$\vec f = \frac{1}{4\pi}[rot\vec B \times \vec B].$ (5.52)

Величина rot $\vec B$ связана с плотностью тока $J$ соотношением

$rot\vec B = \frac{4\pi}{c}\vec J.$ (5.53)

Здесь существенно то, что плотность тока при заданной концентрации заряженных частиц n должна быть ограничена, а именно:

$J < nec = J_{\mbox{крит}}.$ (5.54)

Если конфигурации с магнитными полями изменяются, но так, что эффектом диссипации магнитного поля можно пренебречь, то имеется сохраняющаяся величина, а именно поток магнитной индукции $\vec \Phi$ через заданную поверхность

$\Phi = \int (\vec B d\vec s) \sim BR^2.$ (5.55)

Это явление принято называть вмороженностью, или приклеенностью магнитных силовых линий в веществе. При сжатии звезды с вмороженным магнитным полем величина магнитной индукции В растет как R², т. е. магнитный момент звезды Ξ уменьшается пропорционально радиусу. Таким образом, определяющим параметром скорее является величина потока магнитной индукции Φ , а не магнитный момент Ξ . Но условие сохранения потока магнитной индукции не всегда соблюдается (например, сжатие вдоль магнитного поля его вообще не изменяет), и поэтому в конкретных задачах приходится отдельно обсуждать роль тех или иных определяющих параметров.

Теперь перейдем к поиску связи между различными определяющими параметрами вращения и магнитных полей звезд на основании методов анализа размерностей. Рассмотрим сначала вращающиеся звезды, не учитывая эффекты магнитных полей. Перечислим определяющие параметры для этого случая. Как обычно, здесь надо учитывать основные параметры звезд М, L, R и постоянную тяготения G. Вращение описывается только двумя определяющими параметрами с независимыми размерностями: угловой скоростью вращения Ω;;; и скоростью циркуляционных движений v_c. Момент инерции и момент вращения сразу выражаются через другие параметры и мы используем эти величины только для того, чтобы выяснить физический смысл безразмерных комплексов.

Запишем матрицу размерности для указанных определяющих параметров:

$\begin{matrix} \, & [\Omega] & [v_c] & [M] & [L] & [R] & [G] \\ \mbox{г}&0&0&1&1&0&-1 \\ \mbox{см}&0&1&0&2&1&3 \\ \mbox{сек}&-1&-1&0&-3&0&-2\\ \end{matrix}$

Ранг матрицы равен трем и, следовательно, имеются три безразмерных комплекса с независимыми раз-мерностями. Поскольку мы интересуемся эффектами вращения, выберем, эти безразмерные комплексы так, чтобы в каждый из них входила бы угловая скорость вращения.

При этом условии получаем три безразмерных комплекса. Первый из них, в котором мы не будем учитывать светимость, есть

$\Pi_1 = \frac{\Omega^2 R^2}{GM} = \frac{3}{4\pi}\frac{\Omega^2}{G\bar\rho},$ (5.56)

где $\bar\rho$ средняя плотность звезды. Второй безразмерный комплекс с учетом светимости

$\Pi_2 = \frac{L R}{G\Omega M^2}.$ (5.57)

И, наконец, третий комплекс, включающий циркуляционную скорость, выберем следующим образом:

$\Pi_3 = \frac{v_c} {\Omega^2}\frac{G^2M^3}{L R^5}.$ (5.58)

Численное значение безразмерных комплексов Π₁, Π₂, Π₃ пока остается неопределенным. Обсудим их физический смысл.

Легко видеть, что (5.56), по существу, есть сравнение ускорения силы тяжести на экваторе звезды GM/R² с соответствующим, центробежным ускорением Ω;;;²R. Поскольку для устойчивости звезды необходимо, чтобы центробежная сила всегда была бы существенно меньше силы тяжести, то отсюда следует, что у устойчивых вращающихся звезд Π₁ ≪ 1.

Второй безразмерный комплекс есть отношение энергии, излученной звездой за время одного периода обращения, деленного на 2π, к величине, характеризующей полную гравитационную энергию звезды (т. е. GM²/R). Очевидно, что и этот безразмерный комплекс в устойчивых стационарных звездах много меньше единицы.

Условие малости обоих безразмерных комплексов, Π₁ и Π₂, имеет вполне определенный физический смысл - состояние вращения не зависит от основных параметров звезды и является независимым следствием начальных условий образования звезд. Звезды с одними и теми же значениями М, L и R могут вращаться с различными угловыми скоростями.

Объяснение третьего безразмерного комплекса Π₃ несколько сложнее. Сразу видно, что этот комплекс также независим - его нельзя свести к комплексам Π₁ и Π₂, поскольку ни один из них не включает циркуляционную скорость. С другой стороны, так же сразу видно, что выбор этого комплекса не однозначен, поэтому приведем обоснование для такого выбора. Перепишем (5.58) в виде

$\frac{GM}{R^2}v_c = \frac{\Omega^2 R^3}{GM}\frac{L}{M}\Pi_3$ (5.59)

и учтем, что, по определению, v_c есть циркуляционная скорость, появляющаяся в звездах с лучистым переносом энергии благодаря несовпадению эквипотенциальных уровней (равной суммы гравитационного и центробежного потенциалов) и поверхностей равного потока лучистой энергии.

В (5.59) первый множитель справа есть отношение центробежной силы к силе гравитации, вызывающей это несовпадение поверхностей. Величина GM/R² есть ускорение силы тяжести и поэтому произведение v_cGM/R² есть работа, совершаемая циркуляцией над единицей массы вещества за единицу времени. Наконец, L/M ≈ L_r/M_r есть дивергенция потока лучистой энергии, также отнесенная к единице массы, т. е. как бы "сток" лучистой энергии в данном слое в другие формы энергий - в данном случае в работу циркуляции.

Сопоставляя эти затраты работы, можно считать, что безразмерный комплекс Π₃ должен быть порядка единицы. Более того, подобное соотношение справедливо не только для среднего по всей звезде значения циркуляционной скорости, но и для ее значений в каждой точке внутри звезды. По порядку величины имеем:

$v_c(r) = \frac{\Omega^2 r^2L(r)}{G^2\rho(r)[M(r)]^2}.$ (5.60)

Подробное описание эффекта меридиональной циркуляции дано в книге Шварцшильда [10] и в статье Местеля в сборнике [11]. Первоначально циркуляция из-за вращения рассматривалась как эффективный механизм перемешивания вещества - процесс, важный для определения эволюции звезд. Однако, как следует из (5.59) и (5.60),численное значение скорости циркуляции очень мало (у Солнца - около 10^-9 см ⋅ сек^-1) и только в поверхностных слоях быстровращающихся звезд она может быть заметной, так как v_c ∼ Ω;;;²R⁵. По-видимому, все же роль меридиональной циркуляции в перемешивании звездного вещества и, следовательно, в звездной эволюции невелика.

Из соображений анализа размерностей нетрудно получить и оценку характерного времени выравнивания неоднородности вращения. Здесь есть следующие определяющие параметры: градиент угловой скорости, который мы обозначим через dΩ;;;/dr, с размерностью [dΩ;;;/dr] = см^-1 ⋅ сек^-1, динамическая вязкость η, определенная формулами (5.42) или (5.43), плотность вещества ρ и, наконец, характерное время диссипации t_дисс, в течение которого неоднородное вращение станет приблизительно однородным. Мы выписываем параметры, описывающие условия в данном месте, а не общие параметры звезды, поскольку эффект выравнивания угловых скоростей, - переход к твердотельному вращению, - есть дифференциальный, а не интегральный эффект, характеризующий поведение отдельных частей звезды.

Составляем матрицу размерности:

$\begin{matrix} \, & [\frac{d\Omega}{dr}] & [\eta] & [t] & [\rho] \\ \mbox{г}&0&1&0&1 \\ \mbox{см}&-1&-1&0&-3 \\ \mbox{сек}&-1&-1&1&0 \\ \end{matrix}$

Единственный безразмерный комплекс:

$\Pi = \frac{d\Omega}{dr}\left(\frac{\eta}{\rho}\right)^{1/2}t_{\mbox{дисс}}^{3/2}.$ (5.61)

В случае заметного эффекта выравнивания угловых скоростей из-за действия вязкости этот безразмерный комплекс должен быть порядка единицы. Отсюда характерное время установления твердотельности вращения:

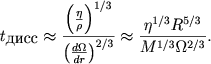
$t_{\mbox{дисс}} \approx \frac{\left(\frac{\eta}{\rho}\right)^{1/3}}{\left(\frac{d\Omega}{dr}\right)^{2/3}} \approx \frac{\eta^{1/3}R^{5/3}}{M^{1/3}\Omega^{2/3}}.$ (5.62)

Эта величина мала по сравнению с характерным временем полной эволюции звезды (у Солнца ~ 5 ⋅ 10⁶ лет), но на ее отдельных этапах нетвердотельность вращения вполне возможна. Например, переход к стадии красного гиганта может быть связан с образованием быстро-вращающегося ядра в центре звезды и гораздо более медленно вращающейся оболочки.

Теперь обратимся к анализу методами теории размерностей условий намагниченности звезд. Прежде всего найдем определяющие параметры. Кроме очевидных величин G, М, R, L следует учесть вращение - параметр Ω;;; и магнитную индукцию В. Магнитные поля, по-видимому, не вызывают каких-либо систематических движений вещества внутри звезд и поэтому здесь нет параметра, аналогичного циркуляционной скорости v_c. Но, с другой стороны, во всех электромагнитных явлениях всегда определяющим параметром должна быть скорость света. Итак, ограничимся следующим набором определяющих параметров: В, Ω;;; , М, R, L, G, с. Отсюда следует матрица размерности:

$\begin{matrix} \, & [B] & [\Omega] & [M] & [R] & [L] & [G] & [c] \\ \mbox{г}&1/2&0&1&0&1&-1&0 \\ \mbox{см}&-1/2&0&0&1&2&3&1 \\ \mbox{сек}&-1&-1&0&0&-3&-2&-1 \\ \end{matrix}$

Ее ранг равен трем и, следовательно, есть четыре независимых безразмерных комплекса. По сравнению с безразмерными комплексами (5.56) - (5.68) здесь, по существу, есть только один новый безразмерный комплекс, связанный с появлением еще одного определяющего параметра. Безразмерные комплексы (5.56) и (5.57) вообще можно оставить без изменения:

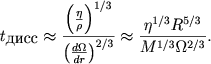
$t_{\mbox{дисс}} \approx \frac{\left(\frac{\eta}{\rho}\right)^{1/3}}{\left(\frac{d\Omega}{dr}\right)^{2/3}} \approx \frac{\eta^{1/3}R^{5/3}}{M^{1/3}\Omega^{2/3}}.$ (5.63)

Как мы уже видели, эти комплексы, по существу, ничего не дают, т. е. угловая скорость вращения не зависит непосредственно от основных параметров, характеризующих звезду. Такой же характер имеет и безразмерный комплекс

$\Pi_3 = \frac{B^2 R^4}{GM^2} = 6\frac{B^2}{8\pi}\frac{4\pi R^3}{3}\frac{R}{GM^2}.$ (5.64)

Здесь В²/8π - характерная величина магнитного давления, a GM²/R⁴ - характерная величина давления, удерживающего звезду в стационарном состоянии. Таким образом, $\frac{B^2}{8\pi}\frac{4\pi}{3}R^3$ есть полная магнитная энергия звезды, a GM³/R - ее гравитационная энергия. Отсюда следует, что Π₃ не мало по сравнению с единицей только у таких звезд, у которых магнитное давление играет существенную роль в балансе всех давлений. Есть ли такие объекты в космических условиях - пока сказать трудно. У Солнца комплекс Π₃ ничтожно мал, у магнитных газовых звезд и пульсаров величина Π₃ также очень мала, порядка 10^-13, так что, вероятно, безразмерные комплексы Π₁, Π₂ и Π₃ для всех реальных звезд есть малые величины и, следовательно, поэтому вряд ли могут служить критериями подобия.

Но, в отличие от безразмерных комплексов (5.63), которые могут меняться не только от звезды к звезде, но и у одной и той же звезды в процессе ее эволюции, безразмерный комплекс (5.64) остается постоянным для данной звезды, если выполнено условие сохранения магнитного потока (5.55). В самом деле, с учетом, (5.55) соотношение (5.64) может быть записано в виде

$\Pi_3 = \Phi^2G^{-1}M^{-2}.$ (5.65)

Все параметры, входящие в безразмерный комплекс (5.65), не меняются в процессе эволюции, если сохраняются условия вмороженности и масса звезды. Аналогичное условие для вращения звезды имело бы место, если бы можно было построить безразмерный комплекс из трех сохраняющихся в процессе эволюции величин $\mathfrak{M}$ (5.41), М и G. Однако это невозможно.

Четвертый безразмерный комплекс включает скорость света:

$\Pi_4 = \frac{cBR}{G^{1/2}M\Omega}.$ (5.66)

Чтобы принять смысл этого безразмерного комплекса, перепишем его в следующем виде:

$\Pi_4 = 2\zeta_n\frac{c\Xi}{G^{1/2}\mathfrak{M}}.$ (5.67)

где мы воспользовались формулами (5.40), (5.41) и (5.45). Напомним, что ζ_n есть безразмерный множитель, определяющий момент инерции тела.

Как уже отмечалось, в реальных звездах безразмерные комплексы Π₁, Π₂ (5.63) и Π₃ (5.64) на много порядков меньше единицы и существенно различны у разных звезд. По-иному ведет себя комплекс Π₄ (5.66). Если подставить сюда численные значения параметров, соответствующих Солнцу или пульсарам, то в обоих случаях получаются близкие по порядку величины значения, сравнимые с 10^-3. Возможно также, что безразмерная величина $\frac{c\Xi}{G^{1/2}\mathfrak{M}}$ и ближе к единице, так как ζ_n обычно мало.

Этот результат уже более интересен. Если принять, что не слишком малая величина отношения $\frac{c\Xi}{G^{1/2}\mathfrak{M}}$ свидетельствует об одинаковости этого отношения для разных объектов, то отсюда следует утверждение о том, что магнитный момент звезды пропорционален ее моменту вращения:

$\Xi \approx A\frac{\sqrt G}{c}\mathfrak{M},$ (5.68)

где А - безразмерная постоянная порядка единицы. Именно такое утверждение было высказано еще в в 1947 г. Блэккетом,. Эта гипотеза в то время много обсуждалась, но в конечном счете была оставлена, поскольку не видно физических явлений, которые приводили бы к пропорциональности между моментом вращения и магнитным моментом у звезд (и планет, по Блэккету) разных типов. Не видно физического обоснования этой гипотезы и сейчас, но соотношения анализа размерностей все же допускают такую зависимость. Важно, что коэффициент пропорциональности между магнитным моментом и моментом вращения выражается только через универсальные постоянные G и с.

В атомной физике тоже имеется универсальная связь между магнитным моментом и моментом вращения (или спиновым моментом) элементарных частиц и атомов. Здесь коэффициент пропорциональности выражается через заряд и массу элементарных частиц. Для тяжелых частиц

$\Xi \approx A\frac{e}{m_p c}\mathfrak{M},$ (5.69)

где А - по-прежнему порядка единицы *).

Отношение размерных коэффициентов пропорциональности в (5.68) и (5.69) равно

$\frac{m_p G^{1/2}}{e} = \left(\frac{\delta}{\alpha}\right)^{1/2},$ (5.70)

где, напоминаем, α и δ - постоянные электромагнитного и гравитационного взаимодействия элементарных частиц.

Все же, по-видимому, соотношение Блэккета (5.68) заслуживает более внимательного изучения. Подсчитаем величину А в (5.68), используя наблюдательные данные по ряду астрономических объектов, не ограничиваясь только звездами.

В табл. 8 даны значения исходных параметров, по которым вычислена величина А из формулы (5.68).

Таблица 8

Объект	B, гс	Ξ , $\frac{\mbox{г}^{1/2}\mbox{см}^{5/2}}{\mbox{сек}}$	$\mathfrak{M}, \, \frac{\mbox{г}\mbox{см}^{2}}{\mbox{сек}}$	A
Земля	0,5	8 ⋅ 10²⁵	5,9 ⋅ 10⁴⁰	0,16
Солнце	2	2 ⋅ 10³²	(1-6) ⋅ 10⁴⁸	0,01
Пульсар	10¹²	5 ⋅ 10²⁹	2 ⋅ 10⁴⁶	0,003
Галактика	10^-6	5 ⋅ 10⁵⁹	2 ⋅ 10⁷³	1

Итак, у разных объектов параметр А заметно различается, но ведь и эти объекты имеют существенно различную природу. Поскольку параметр А во многих случаях мал по сравнению с единицей, то мал и безразмерный комплекс Π₄ (5.67) (так как Π₄ = 2ζ_nA, a ζ_n < 1). Но тем не менее он все же на порядки больше численных значений безразмерных комплексов (5.63) и (5.65). Поэтому (5.66) пока единственная не очень малая безразмерная комбинация, которую можно соста< вить из основных параметров звезды, ее магнитного поля и угловой скорости вращения.

Общеизвестно, что время джоулевой диссипации магнитного поля в космических объектах очень велико, часто на порядки величин больше времени эволюции этих объектов. Соответствующие оценки можно также получить, используя соображения размерности, если учесть следующий набор определяющих параметров: коэффициент магнитной вязкости ν_m (5.49), размер области R, где имеет место затухание, и характерное время затухания t_дисс. Из этих трех величин можно образовать один безразмерный комплекс, из которого следует, что характерное время затухания магнитного поля

$t_{\mbox{дисс}} \approx \frac{R^2}{\nu_m}.$ (5.71)

Мы не включили в число определяющих параметров ни величину В, ни ее градиент типа dB/dr, как это было сделано в аналогичной задаче по определению диссипационного процесса выравнивания угловых скоростей в формуле (5.62). Дело в том, что в данном случае оценивается исчезновение всего поля, которое происходит во всем объеме и не прекращается до тех пор, пока все поле не диссипирует. В соотношениях (5.61) - (5.62) оценивался лишь переход к твердотельному вращению, которое, естественно, определяется градиентом угловых скбростей. Независимость (5.71) от В определяется линейностью уравнений магнитной индукции, описывающих и диссипацию магнитный полей.

Величина ν_m, рассчитанная по молекулярно-кинетической теории, сравнительно мала, и поэтому большие размеры звезд приводят к большому времени затухания. Однако в плазме имеют место разнообразные коллективные процессы, которые могут на много порядков увеличить ν_m (т. е. уменьшить проводимость плазмы). Поэтому с учетом коллективных процессов время диссипации магнитного поля может быть и не столь большим. Анализ всех этих вопросов выходит за рамки настоящей книги.

В заключение настоящего параграфа рассмотрим вопрос о потере момента вращения и магнитного поля звезды благодаря излучению волн. Дело здесь в следующем. Как хорошо известно, вращающийся заряд излучает электромагнитные волны с частотой, равной угловой скорости вращения или ее гармоникам. Очевидно, что вращающийся магнитный диполь тоже должен излучать электромагнитные волны с частотой, равной угловой скорости вращения. Определим мощность излучения таких волн. Сначала будем считать, что вращающийся магнитный диполь с моментом Ξ находится в вакууме, так что ничто не мешает распространению излучаемых им волн. Используем соображения анализа размерностей. Очевидно, что определяющих параметров всего четыре: мощность излучения, которую мы обозначим через L_m, магнитный момент угловая частота вращения Ω;;; и скорость распространения волн с. Матрица размерности имеет следующий вид:

$\begin{matrix} \, & [L_m] & [\Xi] & [\Omega] & [c] \\ \mbox{г}&1&1/2&0&0 \\ \mbox{см}&2&5/2&0&1 \\ \mbox{сек}&-3&-1&-1&1 \\ \end{matrix}$

Имеется только один безразмерный комплекс

$\Pi = L_mc^3\Xi^{-2}\Omega^{-4}.$ (5.72)

Величина Π должна зависеть от геометрии системы. Точный расчет показывает, что диполь, вращающийся вокруг оси вращения под углом, θ к этой оси, излучает электромагнитные волны с мощностью

$L_m = \frac{2}{3}\frac{\Xi^2\Omega^4}{c^3}\sin^2\theta.$ (5.73)

Если считать, что полная светимость пульсара порядка L_m, то, по крайней мере для пульсара в Крабовидной туманности, формула (5.73) дает оценку Ξ ≈ 6 ⋅ 10²⁹ г^1/2см^5/2сек^-1.

На самом деле положение сложнее. Дело в том, что формула (5.73) справедлива лишь для случая, когда скорость распространения электромагнитных волн с частотой Ω;;; близка к с и когда вообще возможно распространение таких волн. Свойства окружающей пульсар плазмы могут существенно изменить условия излучения низкочастотных волн. Например, вращающийся в плазменной среде магнитный диполь излучает также альвеновские волны, скорость распространения которых зависит как от плотности среды, так и от направления распространения. Полная мощность излучения может заметно отличаться от (5.73), в частности, величина L_m может быть пропорциональна и другой степени частоты. Здесь требуется более подробный анализ, и соображения метода размерностей оказываются недостаточными.

Энергия, излучаемая этими волнами, забирается из кинетической энергии вращения, равной ½IΩ;;;². Одно временно эти же волны уносят и момент вращения. Из (5.73) сразу следует, что излучение электромагнитных волн вращающимся магнитным диполем, приводит к торможению вращения, т. е. уменьшению его угловой скорости в соответствии с формулой

$\frac{d\Omega}{dt} = -\frac{2}{3}\frac{\Xi^2\Omega^3}{Ic^3}\sin^2\theta.$ (5.74)

Эту зависимость можно проверить на пульсарах (см. [12]), где, благодаря малой величине периода, можно наблюдать его изменение. Правда, мы не знаем точно ни магнитного момента пульсара Ξ , ни его момента инерции I. Поэтому предположим, что изменение частоты пропорционально ее некоторой степени, т. е.

$\frac{d\Omega}{dt} \sim \Omega^n$ (5.75)

Дифференцируя это соотношение, находим условие

$n = \frac{\Omega}{\frac{d\Omega}{dt}}\frac{d^2\Omega}{dt^2}.$ (5.76)

Каждая из величин в правой части в принципе может быть определена из наблюдений. В 1975 г. данных наблюдений было еще недостаточно. Уверенно наблюдалась вторая производная лишь у пульсара в Крабовидной туманности. В этом случае оказалось примерно n ≈ 3,5. По другим пульсарам уверенных данных нет, но статистический анализ приводит к среднему значению n ≈ 2,4 [12]. Можно надеяться, что в будущем большие ряды наблюдений пульсаров позволят точнее определить показатель степени в (5.75).

Есть и другие механизмы изменения угловой скорости вращения, например, потеря массы. Но мы рассмотрим более экзотический случай - эффект излучения гравитационных волн вращающейся звездой. Эффективность этого механизма существенно зависит от несферичности звезды, точнее, от величины ее квадрупольного момента, который можно определить величиной

$Q = \chi_nMR^2,$ (5.77)

где численный коэффициент зависящий от распределения массы в звезде и от ее несферичности, может быть очень мал. Найдем мощность излучения гравитационных волн на основе соображений размерности. Определяющими параметрами будут Q, угловая скорость Q, скорость распространения гравитационных волн, равная скорости света c, и постоянная тяготения Ньютона, наряду с самой величиной мощности L_g, которую следует определить. Матрица размерности:

$\begin{matrix} \, & [L_g] & [Q] & [\Omega] & [c] & [G] \\ \mbox{г}&1&1&0&0&-1 \\ \mbox{см}&2&2&0&1&3 \\ \mbox{сек}&-3&0&-1&-1&-2 \\ \end{matrix}$

Единственный безразмерный комплекс:

$\Pi = L_g c^5 G^{-1}Q^{-2}\Omega^{-6}$ (5.78)

Точная формула для мощности излучения гравитационных волн имеет вид [13]

$L_g = \frac{GQ^2}{45c^5}\Omega^6.$ (5.79)

Отсюда изменение угловой скорости при излучении гравитационных волн

$\frac{d\Omega}{dt} = -\frac{1}{45}\frac{GQ^2}{Ic^5}\Omega^5,$ (5.80)

т. е. еще сильнее расходится с наблюденным у пульсаров значением показателя n в (5.75). Не будем обсуждать эти расхождения, но отметим только одно любопытное сопоставление формул (5.79) и (5.74). Имеем для отношения обеих мощностей излучения:

$\frac{L_g}{L_m} = \frac{1}{30\sin^2\theta}\frac{GQ^2\Omega^2}{\Xi^2c^5} = \frac{\chi^2_n}{15\zeta^2_n\sin^2\theta}\frac{G\mathfrak{M}^2}{c^2\Xi^2},$ (5.81)

где использована формула (5.40). Последний множитель в этой формуле есть постоянная величина, если правильно соотношение Блэккета. Безразмерный множитель для данной модели тоже постоянен, хотя обычно он очень мал. Таким образом, если справедлива гипотеза Блэккета о пропорциональности между моментом вращения и магнитным моментом, то отсюда следует пропорциональность между мощностями излучения гравитационных и электромагнитных волн вращающимся магнитным диполем.

*) Н. Р. Сибгатуллин обратил наше внимание еще на один пример, иллюстрирующий гипотезу Блэккета. Формула (5.69) справедлива для соотношения между механическим и магнитным моментами вращающихся наряженных "черных дыр" (решение Керра - Ньюмена). В этом случае под е следует понимать заряд "черной дыры", вместо m_p подставить ее массу, а A = 1.

<< § 5.1 Пульсация переменных звезд | Оглавление | § 5.3 Турбулентность и конвекция >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце