<< 4.4. Барицентрическая система координат | Оглавление | 4.6. Приливы и определение >>

4.5. Земная система координат

Международная земная система отсчета (International Terrestrial Reference System - ITRS), по определению, есть геоцентрическая система с началом в центре масс Земли, включая океаны и атмосферу. Единицей длины является метр. Шкалой координатного времени локальной геоцентрической системы является шкала TCG (Geocentric Coordinate Time) (см.§ 5.5.2). Ориентация осей ITRS согласована с результатами наблюдений движения полюса Международной службы широты (предшественницей МСВЗ). Ось является средней осью вращения Земли, направленной в опорный полюс МСВЗ (IERS Reference Pole - IRP), который в свою очередь в пределах ошибок наблюдений совпадает с условным международным началом (Conventional International Origin - CIO). Это было сделано для того, чтобы избежать появления скачков в движении полюса при замене систем координат. Условное международное начало, по определению, это среднее положение земного полюса по измерениям на интервале с 1900 по 1905 гг.

Ось ITRS лежит в плоскости опорного меридиана (IERS Reference Meridian - IRM).

Стабильность положения осей ITRS определяется принятием условия отсутствия глобального вращения коры Земли из-за горизонтальных тектонических движений.

Международная земная система координат (International Terrestrial Reference Frame - ITRF) реализуется декартовыми координатами ряда пунктов. В настоящее время стандартами Международной службы вращения Земли рекомендуется использовать систему ITRF2000. В этой системе координаты и скорости пунктов приводятся на эпоху 1997.0, тогда как плоскость экватора системы на эпоху J2000.0. Если необходимо получить географические координаты , отнесенные к эллипсоиду, то согласно стандартам МСВЗ необходимо использовать эллипсоид GRS80.

Точность наблюдений современными средствами настолько высока, что позволяет определить скорости пунктов, то есть изменение их координат из-за тектонических движений, в течение достаточно короткого промежутка времени (около года).

В качестве примера на рис. 4.8 показано изменение длины базы (расстояния между двумя радиотелескопами) в Ветзеле (Германия) и Вестфорде (США). Из рисунка видно, что метод РСДБ позволяет уверенно определять межконтинентальные расстояния с миллиметровой точностью.

Так как оси системы координат определяются координатами пунктов, то изменение последних может привести к повороту системы координат. Чтобы этого не было (непредсказуемое вращение системы координат может быть интерпретировано как изменение параметров вращения Земли), на скорости пунктов накладывается дополнительное условие: кора Земли не должна иметь вращения относительно земной системы координат. Математически это условие можно записать в виде:

где - радиус-вектор элемента массы в геоцентрической системе координат, - вектор мгновенной угловой скорости вращения Земли. Интегрирование проводится по объему деформируемой части Земли. Во вращающейся системе имеем:

где v - вектор скорости деформации. Уравнение (4.24) эквивалентно выражению:

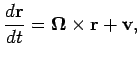
Оси выбранной таким образом системы называются осями Тиссерана^4.2.

Рассмотрим, почему оси Тиссерана так важны при определении земной системы координат. Если тело не является абсолютно твердым, то движение элемента массы вокруг центра масс разделяется на вращение со скоростью и остаточную деформацию со скоростью . Угловой момент тела, который по определению равен

в нашем случае равняется

где

называется относительным угловым моментом. Используя определение тензора инерции , имеем

Предположим, что , и . Это означает, что поле скоростей деформации создается вращением тела с угловой скоростью , и

Таким образом, имеем:

т.е. разложение движения тела на вращательное и деформационное движения неоднозначно. Если , то , т.е. поле скоростей деформации не содержит вращения; измеряемый вектор мгновенной угловой скорости вращения Земли в этом случае не содержит добавок из-за деформации коры Земли.

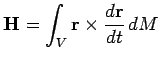
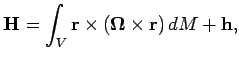
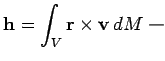
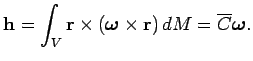
Можно показать, что при выборе осей, в которых , удовлетворяется условие (4.25). Таким образом, относительный угловой момент, вызываемый деформацией тела, в осях Тиссерана равен нулю. На практике при уравнивании наблюденных скоростей пунктов используется условие (4.25).

В разные моменты времени ориентация осей Тиссерана может быть различной, так как поле скоростей деформации меняется. Поэтому при определении системы ITRF обязательно указывается эпоха, к которой относятся координаты и скорости пунктов.

В осях Тиссерана вектор скорости отдельного пункта равен: , где - вектор скорости, определяемый тектоническим движением плиты, на которой располагается пункт наблюдения, - вектор остаточной скорости. Согласно кинематической модели движения плит NNR-NUVEL-1A, вся поверхность Земли разбита на 16 плит, каждая из которых вращается, но суммарное вращение земной коры равно нулю. Обозначение NNR (no-net-rotation) говорит об отсутствии глобального вращения земной коры.

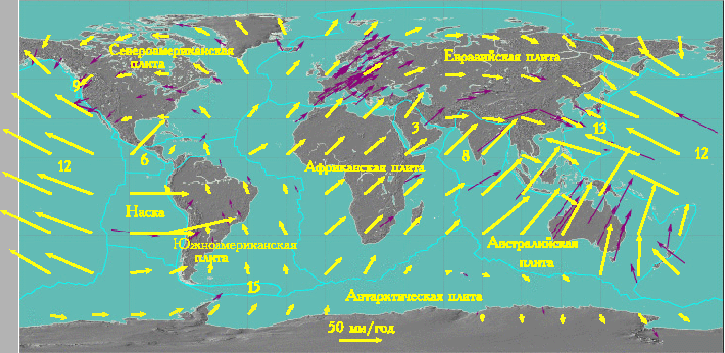
Темными стрелками на рис. 4.9 показаны измеренные с помощью GPS-приемников скорости пунктов, светлыми - скорости, вычисленные по модели движения плит NNR-NUVEL-1A.

Из рис. 4.9 видно достаточно хорошее согласии модели движения плит и наблюдений, за исключением регионов на границах плит. Названия плит, номера которых указаны на рис. 4.9, приводятся в таблице 4.2.

Изменение координат -го пункта наблюдения вычисляется по формуле:

где -положение и скорость телескопа, расположенного в -м пункте, на эпоху определения ориентации ITRF. Поправки к координатам пункта вычисляются на основе моделей приливов в твердой Земле (могут достигать см) и океанических приливов ( см), переменной атмосферной нагрузки на кору Земли ( см), термического расширения телескопа и т.д.

В декартовых координатах изменение координат -го пункта, расположенного на -ой плите (4.26), записывается в виде:

где -компоненты угловой скорости -ой плиты. Угловые скорости плит (модель NNR-NUVEL-1A) приводятся в таблице 4.2.

---

<< 4.4. Барицентрическая система координат | Оглавление | 4.6. Приливы и определение >>

Публикации с ключевыми словами: астрометрия - сферическая астрономия - системы координат - шкалы времени Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
См. также: Константину Владиславовичу Куимову – 75 лет Саймон Ньюком (1835 -1909) к 175-летию со дня рождения. Вращение Земли и продолжительность суток 80 лет со дня рождения Альберта Петровича Гуляева Руководство по практической работе с каталогом Hipparcos К 70-летию Вилена Валентиновича Нестерова Полная версия "Сферической астрономии" В.Е.Жарова Все публикации на ту же тему >>