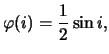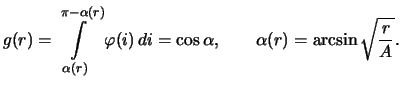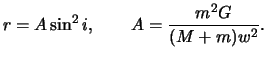О распределении больших полуосей орбит внесолнечных планет
<< 2. Основные соотношения
| Оглавление |
4. Функции распределения >>
Фиксируем
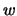
,
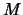
,
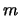
, а тем самым и
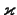
. Тогда
(
2) представит собой неравенство, выделяющее на плоскости
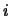
,

(рис.
1) область обнаружимости
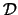
,
расположенную между отрезком
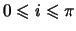
оси
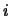
и
кривой:
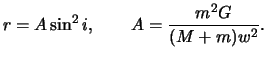 |
(3) |
Следуя [
3],
примем, что все ориентации вектора площадей равновероятны, что влечет
[
1, § 17]
где
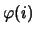
- плотность вероятности случайной величины
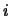
.
Здесь и ниже мы не будем вводить разных обозначений для случайной
величины и переменной, пробегающей ее значения.
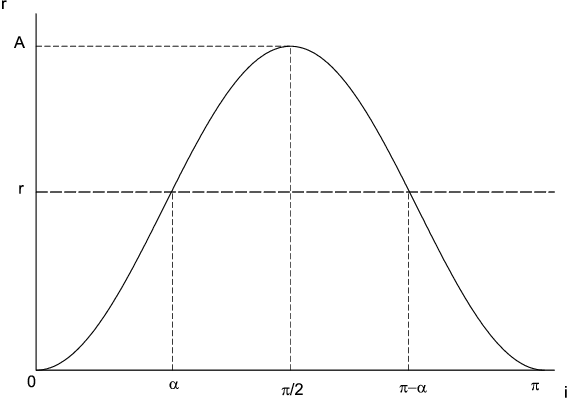 |
Рис. 1.
Критичеcкая кривая (3) |
Вероятность
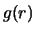
того, что находящаяся на расстоянии

планета будет
открыта по наблюдениям лучевой скорости, обращается в нуль при
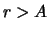
; в
противном случае
Окончательно,
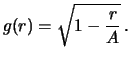 |
(4) |
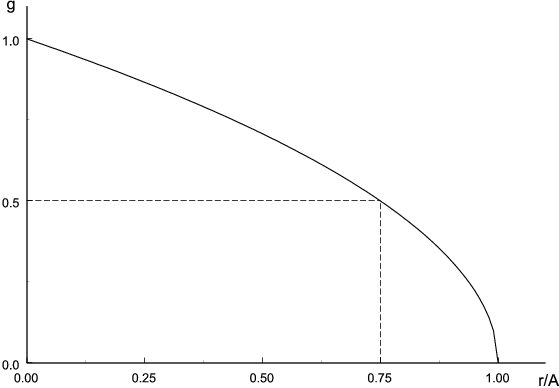
График
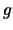
(рис.
2) - часть параболы с вершиной в
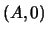
.
Самая левая часть графика
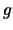
не имеет реального смысла:
следует исключить радиус звезды с некоторым запасом.
<< 2. Основные соотношения
| Оглавление |
4. Функции распределения >>