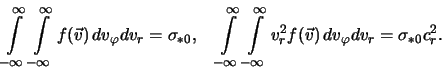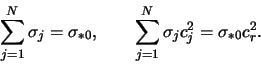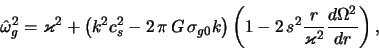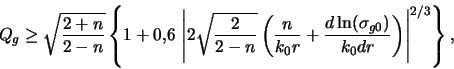<< 2.2 Динамика возмущений ... | Оглавление | 2.4 Условие грав. устойчивости >>
- 2.3.1 Самогравитация
- 2.3.2 Хаотическое движение
- 2.3.3 Вращение
- 2.3.4 Функция распределения звезд по скоростям. Звездно-газовые системы
- 2.3.5 Конечная толщина диска
- 2.3.6 Дифференциальность вращения
- 2.3.7 Неоднородный диск
- 2.3.8 Обсуждение
2.3 Физика гравитационной неустойчивости
Главным "возмутителем спокойствия" в изучаемых нами дисках является гравитация. Гравитационное взаимодействие между разными частями системы (часто говорят "самогравитация") сжимает вещество, оно стремится упасть само на себя. Этот процесс называют гравитационной или джинсовской неустойчивостью. Он приводит к перераспределению массы -- в одной области плотность растет, в другой по необходимости уменьшается. Ряд факторов противостоит самогравитации, другие помогают ей. Прежде чем перейти в следующих разделах к строгому изложению, обсудим физику гравитационной неустойчивости, попытаемся качественно понять, как различные свойства системы влияют на стремление самогравитации "сжать вещество в точку". Джинсовская неустойчивость обладает схожими чертами в звездном и газовом дисках, поэтому мы рассмотрим здесь и газовую систему (см. подробнее гл. 4), тем более, что она для анализа проще. При этом нагляднее проявятся и различия между ними и выяснится, какое влияние на гравитационную устойчивость звездного диска может оказать газовая подсистема. Для нас сейчас все отличие газа от звезд заключается в столкновительности первого, тем самым он описывается уравнениями газодинамики.
Все формулы данного раздела будут получены в последующем,
поэтому сейчас укажем только основные приближения, в рамках
которых они получены. Это эпициклическое приближение [см.
(2.1.13)], диск считается тонким [см. (2.1.11)], возмущения лежат
в плоскости диска и являются коротковолновыми [см. (2.2.16)].
Отметим, что все приведенные здесь соотношения для звездного диска
вытекают из дисперсионного уравнения (2.2.38), а для газового -- из
(4.3.15). Индексы "![]() ", "
", "![]() " в этом разделе указывают соответственно
на принадлежность величины к звездному или газовому диску. Для
составления всестороннего понимания механизма гравитационной
неустойчивости рекомендуем также обратиться к
монографиям Поляченко и Фридмана [1,2], Рольфса [89], Саслау [205].
" в этом разделе указывают соответственно
на принадлежность величины к звездному или газовому диску. Для
составления всестороннего понимания механизма гравитационной
неустойчивости рекомендуем также обратиться к
монографиям Поляченко и Фридмана [1,2], Рольфса [89], Саслау [205].
2.3.1 Самогравитация
Пренебрежем влиянием всех факторов, кроме самогравитации,
т.е. рассмотрим плоский холодный2.9 бесконечно тонкий
гравитирующий слой2.10.
В такой модели при сжатии не возникает
противодействующей силы. Вещество, ускоряясь, падает на область повышенной
плотности, все более увеличивая величину плотности и тем самым силу
притяжения. Развивается гравитационная неустойчивость (коллапс),
частота возмущений которой является чисто мнимой
Ниже мы будем последовательно включать в рассмотрение учет хаотического движения частиц, вращения диска, различных неоднородностей равновесных величин и т.п. Некоторые факторы делают диск более неустойчивым (увеличивают инкремент), и их естественно называть дестабилизирующими. Другие приводят к уменьшению инкремента вплоть до стабилизации гравитационной неустойчивости.
2.3.2 Хаотическое движение
Как хорошо известно, если рассмотренные выше две
гравитационно взаимодействующие частицы обладают моментом
количества движения (первоначально движутся не вдоль одной
прямой), то такое относительное "случайное" движение может
предотвратить столкновение. При переходе к системе с большим
количеством частиц роль этих случайных движений выполняет тепловое
движение ("температура"), и оно работает против гравитационного
скучивания. Если возникает область повышенной плотности размером
![]() , то звезды за счет случайного движения могут покинуть
опасную зону, уменьшить плотность в ней, и тем самым остановить
падение окружающего вещества. Условием устойчивости является
превышение типичной скорости звезды
, то звезды за счет случайного движения могут покинуть
опасную зону, уменьшить плотность в ней, и тем самым остановить
падение окружающего вещества. Условием устойчивости является
превышение типичной скорости звезды ![]() над характерной скоростью
гравитационного падения
над характерной скоростью
гравитационного падения
![]() ,
что приводит к требованию
,
что приводит к требованию
![]() . Естественно,
малое по размеру возмущение легче стабилизируется хаотическим движением.
В случае газа аналогичную оценку можно получить из условия равенства
характерного времени гравитационного падения и времени прохождения
через область размером
. Естественно,
малое по размеру возмущение легче стабилизируется хаотическим движением.
В случае газа аналогичную оценку можно получить из условия равенства
характерного времени гравитационного падения и времени прохождения
через область размером
![]() звуковой волны в газе. При
возникновении сжатия начинает распространяться звуковая волна. Если
характерное время гравитационного нарастания
звуковой волны в газе. При
возникновении сжатия начинает распространяться звуковая волна. Если
характерное время гравитационного нарастания ![]() превышает период
колебаний
превышает период
колебаний
![]() , то возмущения устойчивы:
на быстро движущуюся волну вещество падать не успевает. Опираясь на
эту оценку, можно попытаться обобщить (2.3.1) на случай конечных значений
, то возмущения устойчивы:
на быстро движущуюся волну вещество падать не успевает. Опираясь на
эту оценку, можно попытаться обобщить (2.3.1) на случай конечных значений
![]() :
:
2.3.3 Вращение
Учет вращения превращает плоский слой в собственно диск и
делает устойчивыми длинноволновые осесимметричные (![]() )
возмущения. Это легко понять из следующих рассуждений. Если
область размером
)
возмущения. Это легко понять из следующих рассуждений. Если
область размером
![]() твердотельно вращающегося с угловой
скоростью
твердотельно вращающегося с угловой
скоростью ![]() однородного диска сжать на
однородного диска сжать на
![]() , то
в силу закона сохранения момента импульса вещество на радиусе (
, то
в силу закона сохранения момента импульса вещество на радиусе (![]() ) будет вращаться с
) будет вращаться с
![]() .
В результате появляется возвращающая центробежная сила
.
В результате появляется возвращающая центробежная сила
![]() с точностью
до малого
с точностью
до малого
![]() . Если мы сравним ее с дополнительной
гравитационной силой притяжения, связанной со сжатием диска
. Если мы сравним ее с дополнительной
гравитационной силой притяжения, связанной со сжатием диска
![]() , то увидим, что устойчивы
будут только крупномасштабные возмущения
, то увидим, что устойчивы
будут только крупномасштабные возмущения
![]() . Дисперсионное соотношение для звуковых волн во
вращающейся среде имеет вид
. Дисперсионное соотношение для звуковых волн во
вращающейся среде имеет вид
![]() (первое
слагаемое описывает эпициклические колебания), и уравнения (2.3.1),
(2.3.2) можно обобщить:
(первое
слагаемое описывает эпициклические колебания), и уравнения (2.3.1),
(2.3.2) можно обобщить:
определяют границу устойчивости. Решение системы (2.3.4) не вызывает затруднений, и
 |
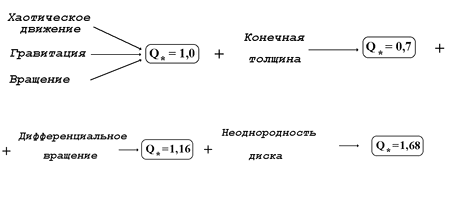
Рис. 2.1. Зависимость частоты джинсовских колебаний
|
Хотя для бесстолкновительного звездного диска дисперсионное
уравнение имеет более сложный вид, условие устойчивости мало
отличается от случая газового диска. На рис. 2.1,в,г показаны две
джинсовские ветви в области
![]() 2.11.
Они аналогичны гравитационным ветвям газового диска (рис. 2.1,а,б), но их
поведение различается в области малых длин волн. Различие связано
с особенностями хаотического движения в столкновительной и
бесстолкновительной системах. В первой возникают звуковые волны,
во второй для мелкомасштабных возмущений случайное движение не
приводит к волновому процессу, и закон дисперсии определяется вращением
2.11.
Они аналогичны гравитационным ветвям газового диска (рис. 2.1,а,б), но их
поведение различается в области малых длин волн. Различие связано
с особенностями хаотического движения в столкновительной и
бесстолкновительной системах. В первой возникают звуковые волны,
во второй для мелкомасштабных возмущений случайное движение не
приводит к волновому процессу, и закон дисперсии определяется вращением
![]() . Как мы знаем, в системе отсчета,
вращающейся с угловой скоростью
. Как мы знаем, в системе отсчета,
вращающейся с угловой скоростью ![]() , траектория движения звезды
в модели твердотельно вращающегося диска представляет собой окружность
с характерным эпициклическим радиусом
, траектория движения звезды
в модели твердотельно вращающегося диска представляет собой окружность
с характерным эпициклическим радиусом
![]() (см. п. 1.1.3).
Поэтому только возмущения с
(см. п. 1.1.3).
Поэтому только возмущения с
![]() испытывают значительное
влияние случайного движения звезд.
испытывают значительное
влияние случайного движения звезд.
В случае бесстолкновительного диска роль параметра ![]() играет
паpаметp Тоомpе
играет
паpаметp Тоомpе
![]() [202], и для
устойчивости
необходимо
[202], и для
устойчивости
необходимо
![]() . Волновое число удобно нормировать на
величину
. Волновое число удобно нормировать на
величину ![]() (
(
![]() -- эпициклический радиус при
-- эпициклический радиус при
![]() ). Тогда на границе устойчивости (
). Тогда на границе устойчивости (![]() ,
, ![]() )
находятся волны с
)
находятся волны с
![]() (см. рис. 2.1,в). При
(см. рис. 2.1,в). При
![]() , как и в случае газового диска, возмущения с
, как и в случае газового диска, возмущения с ![]() оказываются абсолютно неустойчивыми, поскольку для них
оказываются абсолютно неустойчивыми, поскольку для них
![]() (рис. 2.1,г). Заметим, что поскольку в галактиках
(рис. 2.1,г). Заметим, что поскольку в галактиках
![]() , то
, то
![]() .
.
true mm
2.3.4 Функция распределения звезд по скоростям. Звездно-газовые системы
Устойчивость звездных и газовых дисков определяется
значениями параметров
![]() и
и
![]() соответственно, которые формально совпадают с точностью до
числового коэффициента. Замена
соответственно, которые формально совпадают с точностью до
числового коэффициента. Замена ![]() на
на ![]() обусловлена
бесстолкновительностью системы и конкретным выбором функции распределения
звезд по скоростям
обусловлена
бесстолкновительностью системы и конкретным выбором функции распределения
звезд по скоростям ![]() (2.1.34). Как уже упоминалось, функция вида
(2.1.34) описывает реальные распределения скоростей звезд приближенно
[7,187,206,207].
Связано это со звездообразованием, усиливающимся при прохождении
спиральной волны плотности, бесстолкновительностью системы в
смысле звездно-звездного взаимодействия (проблема релаксации и
начальных условий) и, как следствие, с дискретностью звездного
населения по кинематике. Построение функции распределения
(2.1.34). Как уже упоминалось, функция вида
(2.1.34) описывает реальные распределения скоростей звезд приближенно
[7,187,206,207].
Связано это со звездообразованием, усиливающимся при прохождении
спиральной волны плотности, бесстолкновительностью системы в
смысле звездно-звездного взаимодействия (проблема релаксации и
начальных условий) и, как следствие, с дискретностью звездного
населения по кинематике. Построение функции распределения ![]() непосредственно из наблюдений в солнечной окрестности Галактики
дает систематическое отклонение от (2.1.34) [187,206]. Как и ранее,
считаем диск бесконечно тонким и однородным. По определению,
функция распределения удовлетворяет условиям
непосредственно из наблюдений в солнечной окрестности Галактики
дает систематическое отклонение от (2.1.34) [187,206]. Как и ранее,
считаем диск бесконечно тонким и однородным. По определению,
функция распределения удовлетворяет условиям
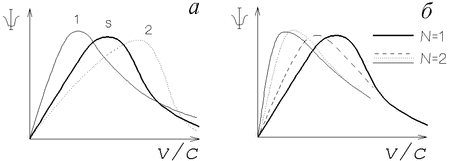 |
Рис. 2.2. Функции распределения длины вектора скорости
|
Одну и ту же дисперсию скоростей можно создать различным
распределением скоростей. Обсудим, как могут повлиять возможные
отклонения функции распределения от шварцшильдовской ![]() (2.1.34).
На рис. 2.2,а изображены два качественно разных случая,
различающихся избытком медленных звезд
(2.1.34).
На рис. 2.2,а изображены два качественно разных случая,
различающихся избытком медленных звезд ![]() и их недостатком
и их недостатком ![]() в
сравнении с функцией
в
сравнении с функцией ![]() . Во всех трех случаях величина
. Во всех трех случаях величина ![]() по
(2.3.5) одна и та же. Для гравитационной устойчивости модели с
по
(2.3.5) одна и та же. Для гравитационной устойчивости модели с ![]() ,
чтобы стабилизировать подсистему медленных частиц, требуется в
целом сильнее разогреть систему, т.е. минимально необходимая для
устойчивости дисперсия скоростей
,
чтобы стабилизировать подсистему медленных частиц, требуется в
целом сильнее разогреть систему, т.е. минимально необходимая для
устойчивости дисперсия скоростей
![]() должна превышать
должна превышать ![]() . В
случае с
. В
случае с ![]() для устойчивости будет достаточно
для устойчивости будет достаточно
![]() .
.
Звездное население дисков плоских галактик можно разбить на ![]() подсистем, каждая из которых характеризуется своей поверхностной
плотностью
подсистем, каждая из которых характеризуется своей поверхностной
плотностью ![]() и дисперсией
и дисперсией ![]() , так что в силу (2.3.5)
, так что в силу (2.3.5)
Предположим, что каждая подсистема описывается шварцшильдовским
распределением
![]() .
На рис. 2.2,б показаны функции распределения длины вектора скорости
.
На рис. 2.2,б показаны функции распределения длины вектора скорости
![]() для
для ![]() ,
, ![]() пpи различных отношениях
пpи различных отношениях
![]() и
и
![]() . Под холодной и маломассивной подсистемой (
. Под холодной и маломассивной подсистемой (
![]() и
и
![]() ) можно понимать молодые звезды. Для гравитационной
стабилизации такой модели необходимо в целом сильнее разогреть
систему
) можно понимать молодые звезды. Для гравитационной
стабилизации такой модели необходимо в целом сильнее разогреть
систему
![]() . Очевидно, что при
. Очевидно, что при ![]() любое
соотношение наборов
любое
соотношение наборов ![]() ,
, ![]() [естественно, удовлетворяющих условиям
(2.3.6)] дает более неустойчивый диск по сравнению с
[естественно, удовлетворяющих условиям
(2.3.6)] дает более неустойчивый диск по сравнению с ![]() ,
поскольку в таких моделях всегда имеется избыток холодных звезд.
,
поскольку в таких моделях всегда имеется избыток холодных звезд.
Расчеты с наблюдаемой функцией распределения скоростей звезд вблизи Солнца говорят о том, что поправка эта невелика и составляет не более 15%.
В рамках обсуждаемого здесь подхода рассмотрим звездно-газовый
диск. Характерная скорость газовых облаков ![]() существенно
меньше дисперсии скоростей звезд
существенно
меньше дисперсии скоростей звезд ![]() . Кроме того,
. Кроме того,
![]() .
С этой точки зрения учет газовой подсистемы эквивалентен наличию молодых
звезд, что, как мы видели, является дестабилизирующим фактором
(см. подробнее п. 6.1.1).
.
С этой точки зрения учет газовой подсистемы эквивалентен наличию молодых
звезд, что, как мы видели, является дестабилизирующим фактором
(см. подробнее п. 6.1.1).
2.3.5 Конечная толщина диска
Чтобы ответить на принципиальный вопрос о том, является
конечная толщина диска ![]() стабилизирующим или дестабилизирующим
фактором, обратимся к уравнению (2.3.1) и запишем его в виде
стабилизирующим или дестабилизирующим
фактором, обратимся к уравнению (2.3.1) и запишем его в виде
![]() , где средняя плотность
, где средняя плотность
![]() . Естественно, оно справедливо только в пределе
. Естественно, оно справедливо только в пределе
![]() . Мы показали в п. 2.3.1, что в
обратном пределе
. Мы показали в п. 2.3.1, что в
обратном пределе
![]() справедливо
справедливо
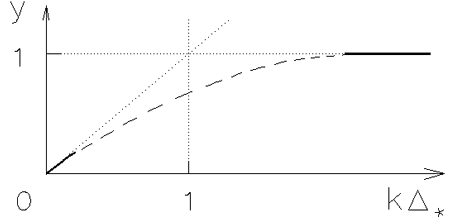
![]() . Как видно из рис. 2.3, следует ожидать стабилизирующего влияния
толщины диска на его гравитационную устойчивость. Действительно, величина
. Как видно из рис. 2.3, следует ожидать стабилизирующего влияния
толщины диска на его гравитационную устойчивость. Действительно, величина
![]() и поверхностная плотность
и поверхностная плотность ![]() входят в дисперсионное
уравнение (2.2.38) только в комбинации
входят в дисперсионное
уравнение (2.2.38) только в комбинации
![]() , что
уменьшает инкремент при
, что
уменьшает инкремент при
![]() . Поскольку наиболее неустойчивые
возмущения обладают
. Поскольку наиболее неустойчивые
возмущения обладают
![]() , можно обобщить критерий
устойчивости звездного диска с учетом
, можно обобщить критерий
устойчивости звездного диска с учетом ![]() и записать
и записать
2.3.6 Дифференциальность вращения
Выше рассматривались осесимметричные колебания ![]() , что
оправданно для однородного твердотельно вращающегося диска,
поскольку учет неосесимметричных возмущений [
, что
оправданно для однородного твердотельно вращающегося диска,
поскольку учет неосесимметричных возмущений [
![]() ] приводит только к допплеровскому сдвигу частоты
] приводит только к допплеровскому сдвигу частоты
![]() и не
сказывается на устойчивости. В дифференциально вращающемся диске с
и не
сказывается на устойчивости. В дифференциально вращающемся диске с
![]() осесимметричные возмущения описываются
дисперсионным уравнением (2.3.3) для
осесимметричные возмущения описываются
дисперсионным уравнением (2.3.3) для
![]() . Существеннее другое. Зависимость угловой скорости от
. Существеннее другое. Зависимость угловой скорости от ![]() приводит к
тому, что более неустойчивыми становятся неосесимметричные ("косые")
возмущения (
приводит к
тому, что более неустойчивыми становятся неосесимметричные ("косые")
возмущения (
![]() ). Рассмотрим физику этого эффекта
отдельно для звездного и газового дисков.
). Рассмотрим физику этого эффекта
отдельно для звездного и газового дисков.
При построении равновесной модели звездного диска в п. 2.1.2
мы получили
![]() , и для угловой скорости вращения
, и для угловой скорости вращения ![]() , убывающей с
радиусом, выполняется
, убывающей с
радиусом, выполняется
![]() . С учетом дифференциальности
вращения траектория движения звезды становится эллипсом с характерными
масштабами осей
. С учетом дифференциальности
вращения траектория движения звезды становится эллипсом с характерными
масштабами осей
![]() и
и
![]() (рис. 2.4). При движении по эллипсу в среднем скорость
звезды в азимутальном направлении меньше, чем в радиальном, и
неосесимметричные возмущения (в пределе "спицеобразные") труднее
подавить по сравнению с осесимметричными. Дисперсия азимутальных
скоростей определяет упругость среды для косых возмущений, и для
подавления гравитационной неустойчивости необходимо в
(рис. 2.4). При движении по эллипсу в среднем скорость
звезды в азимутальном направлении меньше, чем в радиальном, и
неосесимметричные возмущения (в пределе "спицеобразные") труднее
подавить по сравнению с осесимметричными. Дисперсия азимутальных
скоростей определяет упругость среды для косых возмущений, и для
подавления гравитационной неустойчивости необходимо в
![]() раз сильнее разогреть диск. Таким образом, устойчивость определяется
меньшей из величин
раз сильнее разогреть диск. Таким образом, устойчивость определяется
меньшей из величин ![]() и
и ![]() :
:
Рассмотрим газовый диск. Из-за столкновительности
"макромолекулы" газа не движутся по эпициклам и давление является
изотропным в радиальном и азимутальном направлениях.
Дестабилизирующее влияние дифференциальности вращения связано с
действием двух факторов. Во-первых, меняется закон дисперсии
неосесимметричных звуковых волн (2.3.3). Этот эффект связан с
действием силы Кориолиса. Косые возмущения вызывают радиальную
компоненту силы Кориолиса, причем в первом порядке по
дифференциальности вращения она не зависит от знака ![]() ;
поэтому в дисперсионное уравнение должна входить величина
;
поэтому в дисперсионное уравнение должна входить величина ![]() .
Вычисления дают
.
Вычисления дают
Для плоской кривой вращения (![]() ) имеем
) имеем ![]() 2.12. Оба условия (2.3.8) и
(2.3.10) при
2.12. Оба условия (2.3.8) и
(2.3.10) при
![]() дают бесконечно большие значения
параметра
дают бесконечно большие значения
параметра ![]() , что связано с неустойчивостью круговых орбит для
закона с
, что связано с неустойчивостью круговых орбит для
закона с ![]() . Эта неустойчивость обусловлена видом внешнего
потенциала, не связана с самогравитацией и не может быть подавлена
температурой. Следует сказать, что для систем с
. Эта неустойчивость обусловлена видом внешнего
потенциала, не связана с самогравитацией и не может быть подавлена
температурой. Следует сказать, что для систем с
![]() из-за
нарушения условий, положенных в основу получения данных критериев,
погрешность этих формул может быть
существенной2.13.
из-за
нарушения условий, положенных в основу получения данных критериев,
погрешность этих формул может быть
существенной2.13.
Существует еще один дестабилизирующий фактор, связанный с дифференциальностью вращения, однако рассмотрение его более естественно провести в следующем пункте.
2.3.7 Неоднородный диск
Под неоднородностью диска мы будем понимать зависимость
поверхностной плотности и/или дисперсии скоростей (скорости звука
для газового диска) от радиальной координаты. В однородной системе
имеются две джинсовские ветви колебаний (см. рис. 2.1).
Неоднородность диска (или дифференциальность вращения) приводит к
появлению еще одной ветви колебаний, ее называют градиентной.
Волновой вектор ![]() для этого типа колебаний должен быть направлен
под углом к градиенту равновесной величины. Как правило, чем более
косые возмущения, тем больше частота колебаний. Градиентные волны
обусловлены дополнительной "упругостью" неоднородной среды.
Известно множество примеров проявления таких колебаний в самых
разных областях физики.
для этого типа колебаний должен быть направлен
под углом к градиенту равновесной величины. Как правило, чем более
косые возмущения, тем больше частота колебаний. Градиентные волны
обусловлены дополнительной "упругостью" неоднородной среды.
Известно множество примеров проявления таких колебаний в самых
разных областях физики.
Поверхностные гравитационные волны на поверхности раздела
двух сред (ПГВ) -- наиболее известный тип волн, связанный с
неоднородностью системы, которая вызвана вертикальной силой
тяжести ![]() . Для несжимаемых жидкостей с плотностью
. Для несжимаемых жидкостей с плотностью ![]() и
и
![]() закон дисперсии имеет вид
закон дисперсии имеет вид
![]() .
.
Внутренние гравитационные волны (ВГВ) могут распространяться
в океане или атмосфере Земли из-за неоднородности в вертикальном
направлении объемной плотности вещества ![]() . Для них
. Для них

ПГВ и ВГВ являются поперечными (или сдвиговыми). Сдвиговая упругость среды возникает из-за неоднородности архимедовой силы в
Гравитационно-гироскопические волны (ГГВ) являются примером
крупномасштабных возмущений в океане постоянной глубины ![]() с учетом
вращения планеты с угловой скоростью
с учетом
вращения планеты с угловой скоростью ![]() . Дисперсионное уравнение
для них имеет вид
. Дисперсионное уравнение
для них имеет вид
![]() , здесь
, здесь
![]() . Из условия равновесия
. Из условия равновесия
![]() .
.
Волны Россби связаны с изменением
![]() вдоль географической широты (рис. 2.5):
вдоль географической широты (рис. 2.5):
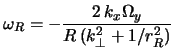 , где
, где
![]() ,
,
![]() . Возвращающей силой является сила Кориолиса.
. Возвращающей силой является сила Кориолиса.
Все эти примеры хорошо известны и легко наблюдаются в природе. Огромное количество волн градиентного типа получено при изучении физики плазмы (их часто называют диффузионными). Таким образом, наличие в неоднородных астрофизических дисках градиентных ветвей колебаний представляется естественным.
Рассмотрение механизма дестабилизирующего влияния
неоднородности для звездного и газового дисков дает качественно
похожие картины. На основе вышеперечисленных примеров видно, что
частота коротковолновых градиентных колебаний приближенно равна
![]() (
(![]() -- характерная скорость хаотических движений,
-- характерная скорость хаотических движений, ![]() --
характерный масштаб неоднородности), т.е. они являются
низкочастотными,
--
характерный масштаб неоднородности), т.е. они являются
низкочастотными,
![]() . Если в какой-то области
длин волн две ветви колебаний имеют близкие друг другу вещественные
частоты, то возможно возникновение между ними "слабой связи" с
появлением
. Если в какой-то области
длин волн две ветви колебаний имеют близкие друг другу вещественные
частоты, то возможно возникновение между ними "слабой связи" с
появлением
![]() , т.е. неустойчивости (см., например,
[209]). В случае гравитационно устойчивого диска с
, т.е. неустойчивости (см., например,
[209]). В случае гравитационно устойчивого диска с ![]() джинсовские
и градиентная ветвь отделены друг от друга (рис. 2.6,а). При уменьшении
параметра
джинсовские
и градиентная ветвь отделены друг от друга (рис. 2.6,а). При уменьшении
параметра ![]() частота гравитационных ветвей уменьшается, и при некоторых
частота гравитационных ветвей уменьшается, и при некоторых
![]() в случае
в случае
![]() отрицательная джинсовская ветвь начинает
взаимодействовать с градиентной, в результате вместо двух
действительных частот появляется два комплексно-сопряженных
(рис. 2.6,б). Решение с
отрицательная джинсовская ветвь начинает
взаимодействовать с градиентной, в результате вместо двух
действительных частот появляется два комплексно-сопряженных
(рис. 2.6,б). Решение с
![]() соответствует
гравитационно-градиентной неустойчивости. Градиентная ветвь может при
определенных условиях взаимодействовать и/или с положительной
джинсовской (см. рис. 2.6,в). Градиентные колебания могут быть
обусловлены не только неоднородностью, но и дифференциальным
вращением. Это ярко видно на приведенном выше примере волн Россби
для газа.
соответствует
гравитационно-градиентной неустойчивости. Градиентная ветвь может при
определенных условиях взаимодействовать и/или с положительной
джинсовской (см. рис. 2.6,в). Градиентные колебания могут быть
обусловлены не только неоднородностью, но и дифференциальным
вращением. Это ярко видно на приведенном выше примере волн Россби
для газа.
 |
Рис. 2.6. Дисперсионные кривые для неосесимметричных возмущений
( |
Для газового диска при типичных условиях дестабилизация
системы за счет эффектов взаимодействия градиентной и джинсовских
колебаний невелика. Условие (2.3.10) принимает вид
Для звездного диска с учетом всех рассмотренных нами факторов
запишем аналогичное условие
В заключение отметим, что в газовом диске может существовать
еще одна ветвь колебаний -- энтропийная. В модели с равновесной
энтропией
![]() const частота этих колебаний
const частота этих колебаний
![]() . Если
. Если
![]() , то это приводит к новой энтропийной ветви колебаний.
Естественно, она относится к градиентному типу и является
низкочастотной. Ее взаимодействие с джинсовскими ветвями вносит
дополнительное дестабилизирующее влияние.
, то это приводит к новой энтропийной ветви колебаний.
Естественно, она относится к градиентному типу и является
низкочастотной. Ее взаимодействие с джинсовскими ветвями вносит
дополнительное дестабилизирующее влияние.
2.3.8 Обсуждение
Гравитационная устойчивость плоских систем относительно
мелкомасштабных возмущений определяется действием разнообразных
факторов. Примечательно, что критерий локальной устойчивости можно
записать в виде достаточно простого условия
![]() [см.
(2.3.11), (2.3.12)]. Значение параметра
[см.
(2.3.11), (2.3.12)]. Значение параметра
![]() является ключевым
для рассматриваемой проблемы. Совместное действие самогравитации,
вращения и хаотического движения частиц требует
является ключевым
для рассматриваемой проблемы. Совместное действие самогравитации,
вращения и хаотического движения частиц требует
![]() (рис. 2.7). Конечная
толщина диска уменьшает это значение, а зависимости равновесных
величин от радиальной координаты в целом приводят к
(рис. 2.7). Конечная
толщина диска уменьшает это значение, а зависимости равновесных
величин от радиальной координаты в целом приводят к
![]() . Для
примера рассмотрим солнечную окрестность звездного диска
Галактики. Для оценок примем:
. Для
примера рассмотрим солнечную окрестность звездного диска
Галактики. Для оценок примем:
![]() M
M![]() /пк
/пк![]() ,
, ![]() км/с/кпк,
км/с/кпк,
![]() ,
, ![]() пк,
пк, ![]() кпк,
кпк,
![]() кпк и, следовательно,
кпк и, следовательно, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() км/с. Подставляя значения этих
параметров в (2.3.12), получим
км/с. Подставляя значения этих
параметров в (2.3.12), получим
![]() . Интересно проследить, как
тот или иной фактор меняет значение
. Интересно проследить, как
тот или иной фактор меняет значение
![]() (рис. 2.7).
Условие
(рис. 2.7).
Условие
![]() приводит к значениям
приводит к значениям
![]() км/с;
это означает, что звездный
диск в окрестности Солнца находится на границе гравитационной
устойчивости.
км/с;
это означает, что звездный
диск в окрестности Солнца находится на границе гравитационной
устойчивости.
<< 2.2 Динамика возмущений ... | Оглавление | 2.4 Условие грав. устойчивости >>
|
Публикации с ключевыми словами:
аккреционный диск - диск, галактический - гидродинамика - спиральная структура
Публикации со словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура | |
См. также:
Все публикации на ту же тему >> | |