Глава IV. Принцип подобия в численном моделировании стационарных звезд
В настоящей главе мы продолжим анализ свойств звезд уже на основе принципа подобия. Это позволит получить более детальные характеристики, в частности, определить и численные значения безразмерных комплексов.
Разумеется, настоящая глава не претендует на сколько-нибудь полное изложение теории внутреннего строения звезд. Основное внимание уделяется условиям подобия звездных моделей.
Весь анализ структуры и эволюции звезд основан на численном моделировании. Уравнения внутреннего строения звезд относительно просты и поэтому их численное решение было нетрудно получить еще до наступления "эры ЭВМ". Создание быстродействующих ЭВМ дало возможность построить большое число звездных моделей, анализ и сравнение с наблюдениями которых позволили далеко продвинуться в понимании звездной эволюции.
Сопоставление теории с наблюдениями основано на сравнении теоретических зависимостей между основными параметрами звезд (масса М, светимость L, радиус R) и подобными же статистическими данными, полученными на основе наблюдений большого числа звезд. В частности, особое значение имеет статистический анализ групп звезд, связанных общностью происхождения, например, входящих в галактические скопления. Правда, такие сопоставления не всегда достаточно критичны, поскольку теоретические зависимости между М, L и R в некоторых случаях слабо зависят от выбора теоретических моделей. Уже отмечалось, что соотношение масса - светимость почти не зависит от выбора закона выделения энергии. Но тем не менее важно подчеркнуть, что теоретические и наблюдаемые зависимости между М, L и R, как правило, хорошо согласуются между собой.
Есть две более непосредственные наблюдательные проверки теории строения звезд: по движению линии апсид в тесных двойных системах и по нейтринному излучению Солнца. Метод определения степени неоднородности модели (концентрации плотности к центру) по движению линии апсид подробно описан, например, в книге Шварцшильда [1]. Здесь также теория оказалась в хорошем согласии с наблюдениями, но и этот метод сравнения недостаточно критичен. Кроме того, его удалось пока применить к очень небольшому числу звезд только верхней части главной последовательности. Более интересна проверка по нейтринному излучению, хотя она, по крайней мере пока, может быть использована только для анализа моделей Солнца. Измеряя поток нейтрино от Солнца, можно непосредственно судить об условиях в его центральных частях. Как хорошо известно, эксперименты Девиса привели к заметному расхождению теории и наблюдений (последний обзор всей этой проблемы изложен в работах [2, 3]). Пока (1975 г.) не ясно, как удастся преодолеть эту трудность, сохранив наши основные представления о характере и роли различных термоядерных реакций в звездах и об их строении и эволюции. Но мы в дальнейшем будем считать эти представления правильными.
Анализ численных моделей строения звезд дал очень многое и было бы весьма неразумно отказываться от этого большого объема информации только из-за того, что мы не можем преодолеть некоторые трудности.
Развитие теории численного моделирования звезд прошло несколько этапов. На первых порах широко использовался принцип подобия - предполагалось, что звезды с разными значениями основных параметров могут иметь подобное строение, описываемое одними и теми же безразмерными уравнениями с одними и теми же значениями безразмерных комплексов. Такое предположение позволило сразу же получить теоретические зависимости между М, L и R, т. е. именно то, что и подлежит сравнению с наблюдениями в первую очередь.
Однако применение принципа подобия налагает определенные ограничения на соотношения, описывающие физические процессы в недрах звезд. К сожалению, при применении принципа подобия в теории строения и эволюции звезд можно использовать только приближенные формулы, описывающие непрозрачность и мощность выделения энергии. Поэтому по мере развития теории все больше и больше появлялось работ по расчетам конкретных моделей. Иными словами, для каждого заданного значения М, L и R и предположенного химического состава рассчитывалась своя модель. Зависимости между этими параметрами теперь уже определяются на основе анализа совокупности этих моделей. Использование мощных ЭВМ сделало расчет большого числа конкретных моделей не слишком трудоемкой работой. Разумеется, такой анализ большого числа конкретных моделей дает более достоверные данные (в рамках сделанных допущений), чем результаты применения принципа подобия, основанные на упрощенных соотношениях. Тем не менее, а особенно учитывая и некоторую имеющуюся неуверенность в исходных предпосылках, представляет определенный интерес и анализ выводов, основанных на методе подобия. Они более наглядны, получаются более простым путем и позволяют яснее понять, в чем могут заключаться те или иные трудности. Здесь мы дадим обзор результатов, полученных в теории внутреннего строения и эволюции звезд путем применения принципа подобия.
§ 4.1 Основные уравнения теории внутреннего строения звезд
Основные уравнения, описывающие внутреннее строение звезд, приводились многократно в специальных монографиях [1, 4, 5] и учебниках [6, 7]. Качественное изложение физического смысла уравнений излагалось и в научно-популярной литературе (см. [8]). Надо также отметить, что был опубликован ряд сборников [9-11], где эти уравнения также подробно описывались. Здесь мы ограничимся лишь кратким пояснением.
Во-первых, предположим сферическую симметричность звезды. Для большинства звезд это условие выполнено с огромной точностью. Даже быстро вращающиеся звезды почти сферически-симметричны. Более заметны отклонения от сферической симметрии у звезд, входящих в тесные двойные системы. Но это особый случай, поскольку нельзя рассматривать строение одной звезды, не обращая внимания на ее компоненту.
Во-вторых, мы будем пренебрегать влиянием магнитного поля на структуру звезды. Это отдельная и, к сожалению, весьма неопределенная проблема, поскольку никаких данных о магнитных полях в недрах звезд у нас нет. Некоторые качественные соображения на основе теории размерностей будут приведены в следующей главе.
В-третьих, мы будем считать звезды стационарными или, по крайней мере, квазистационарными объектами. В действительности любая звезда эволюционирует, но если связанные с этим изменения происходят медленно, то в уравнениях звездной структуры можно опустить члены, явно описывающие изменение параметров со временем.
Теперь запишем сами уравнения. В стационарной звезде имеет место гидростатическое равновесие, описываемое соотношением
|
|
(4.1) |
Здесь р - полное давление вещества и излучения, ρ - плотность вещества, М(r) - масса, заключенная внутри сферы с радиусом r (расстоянием от центра), G - постоянная тяготения. Величина М(r) может быть определена интегральным или дифференциальным соотношением
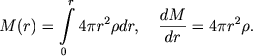
|
(4.2) |
Внутри звезд отклонение от термодинамического равновесия очень мало и поэтому давление вещества и излучения определяется плотностью ρ, температурой газа и равновесного (чернотельного) излучения Т. Для звезд, построенных из обычного газа, т. е. таких, где нет вырождения электронного газа, полное давление складывается из давления идеального газа и давления излучения:
|
|
(4.3) |
где ℜ - универсальная газовая постоянная, μ - молекулярный вес (атомный вес, приходящийся на одну частицу), а - постоянная плотности излучения (![]() ). В недрах звезд водород, гелий и другие не слишком тяжелые элементы ионизованы почти полностью и поэтому для молекулярного веса имеем
). В недрах звезд водород, гелий и другие не слишком тяжелые элементы ионизованы почти полностью и поэтому для молекулярного веса имеем
|
|
(4.4) |
где X - доля водорода, У - доля гелия, Z - доля всех остальных элементов (по весу). Так как X + У + Z = 1 и обычно Z << l, то можно пользоваться второй формулой (4.4).
В белых карликах, а также в центральных частях других звезд электронный газ может быть вырожденным. Выражение для давления нерелятивистского электронного вырожденного газа в случае, когда его температура близка к нулю, было дано формулой (3.44). Теперь приведем соответствующую формулу с учетом температурной поправки:
|
|
(4.5) |
При сильном вырождении электронного газа эта формула оказывается справедливой и при достаточно высокой температуре. Аналогичная формула для релятивистского вырожденного газа имеет вид
|
|
(4.6) |
Здесь μe - молекулярный вес, приходящийся на один электрон. Имеем
|
|
(4.7) |
Надо также учитывать и давление газа, состоящего из атомных ядер. Его можно описать обычным уравнением Клапейрона. Первые члены соотношений (4.5) и (4.6), как мы уже знаем, являются частным случаем уже хорошо известной политропной зависимости между давлением и плотностью:
|
|
Политропное уравнение состояния оказывается очень полезным в применении метода подобия. Но, как следует из приведенных выше формул, в реальных условиях звездного вещества строгое политропное соотношение встречается редко. Однако оказывается, что по крайней мере в некоторых задачах можно сохранить принцип подобия, использовав соотношение
|
|
(4.8) |
где &Kα и α тоже некоторые постоянные. Например, в основной области вырожденного газа в белых карликах или в изотермических вырожденных ядрах звезд-гигантов температура почти одинакова по всей области. Здесь вполне можно использовать (4.8) при α = 1/3 в случае (4.5) и α = 2/3 в случае (4.6).
Переход от нерелятивистского к релятивистскому вырожденному электронному газу можно описать изменением показателя политропы. Например, постепенная релятивизация электронов по мере увеличения плотности может быть учтена заменой показателя 5/3 в (4.5) на величину
![$$
\gamma = \frac{5}{3} \left[1 - \frac{1}{7}\left(\frac{\hbar}{m_e c}\right)^2 \left(\frac{3\pi^2\rho}{\mu_e m_p }\right)^{2/3} + ...\right].
$$](http://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula146.gif)
|
(4.9) |
Аналогичным образом может быть учтена и неполная релятивизация электронов в (4.6) путем замены 4/3 па показатель
![$$
\gamma = \frac{4}{3} \left[1 + \frac{3}{4}\left(\frac{m_e c}{\hbar}\right)^2 \left(\frac{\mu_e m_p }{3\pi^2\rho}\right)^{2/3} + ...\right].
$$](http://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula147.gif)
|
(4.10) |
Разумеется, формулы (4.9) и (4.10) справедливы, пока вторые члены в скобках заметно меньше единицы.
Конкретно, использование соотношений (4.9) и (4.10) может сводиться к следующему. Рассчитываются подобные модели с фиксированным, но неопределенным заранее γ , а затем подбирается величина этого показателя так, чтобы его значение соответствовало бы характерной плоскости вырожденного ядра звезды.
Температура газа и излучения, входящая в уравнение (4.3), определяется условиями переноса энергии. Как правило, источники энергии действуют в центральных частях звезды, и перенос ее наружу оказывается существенным для определения всей структуры звезды. Известно несколько механизмов переноса энергии: конвективный, лучистый, электронной теплопроводностью. Наиболее эффективен механизм конвективного переноса энергии, но он не всегда возможен.
Приведем некоторые основные данные об адиабатическом конвективном переносе энергии, которые понадобятся в этой главе. В глубоких слоях звезды конвекция имеет адиабатический характер. Элемент массы газа, случайно оказавшийся более нагретым, поднимается вверх и расширяется по адиабатическому закону. Другие элементы, более холодные, опускаются вниз, сжимаясь также по адиабатическому закону. Высота подъема или опускания конвективных элементов, называемая длиной перемешивания, обычно порядка эквивалентной высоты распределения плотности или давления.
Поскольку движение газа определяется адиабатической зависимостью, то в области конвективного переноса распределение плотности и давления также должно определяться адиабатическими изменениями, а именно здесь имеет место политропное соотношение, где теперь показатель γ есть отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
Значение показателя γ зависит от степени ионизации газа и от роли лучевого давления. Там, где ионизация почти полная (глубокие слои звезды) и где газ можно считать одиоатомным, показатель γ равен (см. [5])
|
|
(4.11) |
где β - отношение газового давления к полному, т. е.
|
|
(4.12) |
Условие ![]() справедливо при 1 - β ≪ 1. Таким образом, в области переноса энергии конвекцией давление и плотность связаны политропной зависимостью, где показатель, однако, тоже может меняться при изменении β с глубиной. Условие политропной зависимости определяет и градиент температуры в этой области. Лучше записать сразу выражение для логарифмического адиабатического градиента температуры по давлению:
справедливо при 1 - β ≪ 1. Таким образом, в области переноса энергии конвекцией давление и плотность связаны политропной зависимостью, где показатель, однако, тоже может меняться при изменении β с глубиной. Условие политропной зависимости определяет и градиент температуры в этой области. Лучше записать сразу выражение для логарифмического адиабатического градиента температуры по давлению:
|
|
(4.13) |
где показатель γ2 отличается от γ1 в случае большой роли излучения:
|
|
Очевидно, что γ1 = γ2 = 5/3 в случае β = 1. Различие между γ1 и γ2 связано с тем, что при β ≠ 1 вещество звезды представляет собой газ с двумя политропами, как, например, в формуле (4.8) с разными показателями (γ = 5/3, α = 4/3). Формулы (4.14) и (4.13) определяют "эффективные политропные показатели" полного изменения состояния при адиабатических изменениях.
С глубиной величина β меняется (если исключить случай ρ ∼ Т3), как это следует из (4.13). Но это изменение относительно невелико и, кроме того, в реальных звездах всегда β сравнительно близко к единице. Таким образом, конвективный перенос энергии тоже описывается политропой с медленно меняющимся показателем. Более того, эффективная величина γ меняется и благодаря изменению состояния ионизации вещества. Правда, в глубоких слоях звезд, где водород, гелий и другие легкие элементы ионизованы почти полностью, этим эффектом можно пренебречь, но он весьма существен при анализе конвекции в слоях звезд вблизи поверхности. Но здесь важно учитывать и отклонения от адиабатичности. В следующей главе будет несколько подробнее обсуждаться случай конвекции во внешних слоях звезд.
По формуле (4.13) можно определять градиент температуры только в том случае, когда молекулярный вес не меняется. Если учесть и этот эффект, то к ∇ад в (4.13) добавляется еще одно слагаемое:
|
|
Формула (4.13) вместе с формулой (4.1) определяет и градиент температуры по глубине, т. е. величину dT/dr в области переноса энергии адиабатическими конвективными движениями.
Перенос энергии электронной теплопроводностью оказывается существенным лишь в областях, где велико вырождение электронного газа. К этому вопросу мы вернемся, когда будем рассматривать подобные объекты.
Перейдем, наконец, к лучистому переносу энергии, который играет очень важную роль в определении структуры подавляющего большинства звезд, и к анализу источников энергии. Как правило, уравнение лучистого переноса записывается в диффузионном приближении:
|
|
(4.14) |
Здесь Dr - коэффициент диффузии энергии излучения, величина L(r) есть количество энергии, генерируемой внутри сферы радиуса r. По определению,
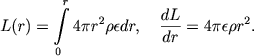
|
(4.15) |
Здесь ε - количество энергии, освобождающейся в единице массы за единицу времени. Коэффициент диффузии лучистой энергии можно выразить через длину свободного пробега квантов l: Dr = 1/3 lc. Вместо l удобно ввести коэффициент непрозрачности ϰ но формуле l = 1/ϰр и переписать соотношение (4.14) в таком виде:
|
|
(4.16) |
Эта форма записи удобна и тем, что 1/3 aT4 есть лучевое давление, а формулы (4.16) и (4.1) имеют аналогичный вид.
Величины ϰ и ε , точнее, их зависимости от параметров среды р и Т и от химического состава, играют большую роль в теории внутреннего строения звезд. Очень много внимания уделялось вычислению этих параметров. Обсуждение этих вычислений и их результаты подробно приводились в цитированных выше монографиях по внутреннему строению звезд и, в частности, в статьях Ривса и Кокса (см. сборник [9]). Коэффициент непрозрачности теперь обычно задается в табличной форме. Для современных расчетов на ЭВМ простые аналитические соотношения уже оказываются недостаточными. Величины ε - мощности источников - еще могут быть записаны в аналитическом виде. Но и здесь некоторые поправочные множители задаются в табличной форме.
Для нашей задачи - применение метода подобия к теории строения звезд - необходимы аналитические формулы для величин ϰ и ε . Более того, эти формулы должны быть простого степенного вида.
Первое приближение в теории переноса энергии излучением приводит к известной формуле Крамерса, уже обсуждавшейся в гл. 2:
|
|
(4.17) |
где величина ϰ0 зависит от химического состава и состояния ионизации. Если концентрация тяжелых элементов Z не слишком мала, то основной вклад в непрозрачность дает взаимодействие электронов с этими элементами:
|
|
(4.18) |
Здесь множитель 1 + X определяет относительное число свободных электронов. С другой стороны, в веществе, состоящем почти исключительно из ионизованных водорода и гелия, основным источником поглощения является торможение электронов в электрическом поле этих ядер и
|
|
(4.19) |
Здесь учтено, что Х + У ≈ 1. Формула (4.19) используется только при Z ≲ 3 ⋅ 10-3.
Качественное объяснение общей зависимости (4.17) легко получить из следующих соображений [4]. Очевидно, что длина свободного пробега кванта должна быть, с одной стороны, пропорциональна плотности излучения, т. е. аТ4, а с другой стороны, должна быть обратно пропорциональна вероятности поглощения кванта. Последняя тем больше, чем больше концентрация электронов и ионов и тепловая скорость электронов vTe ∼ T½. Отсюда имеем
|
|
Подставив это выражение в определение ![]() получаем формулу Крамерса.
получаем формулу Крамерса.
На самом деле коэффициент поглощения зависит от химического состава, плотности и температуры более сложным образом, чем это следует из простой формулы Крамерса. Поэтому для большей общности пользуются таким соотношением
|
|
(4.20) |
где ϰ0(Х, Y, Z), α и ν - некоторые значения параметров, подбираемые из условия лучшего согласия табличных данных с формулой (4.20).
Обычно в основной части недр звезд параметры ν и α меняются не очень сильно. С увеличением температуры ос несколько уменьшается (примерно до α ≈ 0,9-0,8). Показатель ν часто близок к 7/2, но уменьшается с ростом плотности (до ν ≈ 2). Все три параметра зависят и от химического состава.
В очень горячей плазме, где имеет место полная ионизация, основным механизмом непрозрачности является рассеяние света на свободных электронах. Здесь непрозрачность определяется очень простой формулой, также приведенной ранее в гл. 2:
|
|
(4.21) |
Очевидно, что (4.21) можно считать частным случаем (4.20) при α = ν = 0.
Формула Крамерса неприменима и в случае очень низких температур, когда степень ионизации мала. В области температур порядка нескольких тысяч градусов имеем следующие зависимости (см. статью Стейна в сборнике [10]). Для звезд населения первого типа, достаточно богатых гелием и тяжелыми элементами (Х=0,6, Y=0,38, Z=0,02), коэффициент непрозрачности
|
|
(4.22) |
С другой стороны, у звезд населения второго типа, где гелия и, особенно, тяжелых элементов очень мало (Х = 0,9, Y = 0,099, Z = 0,001), коэффициент непрозрачности
|
|
(4.23) |
Эти формулы также можно рассматривать как частные случаи зависимости (4.20), где α ≈ 0,6-0,7, а параметр v оказался очень большим по абсолютной величине и, что самое главное, отрицательным. Еще раз напомним, что соотношения (4.22) и (4.23) применимы только при низких температурах. Общий ход коэффициентов непрозрачности дан на рис. 1. Грубую оценку максимума ϰ можно получить из пересечения кривых (4.22) или (4.23) с (4.17), а минимальное значение ϰ при достаточно высоких температурах определяется (4.21).
Перейдем теперь к определению функции ε - мощности источников энергии. Подробное изложение теории и сводки всех используемых здесь формул даны, например, в статьях Ривса в [9] и [10]. Здесь, как и в случае коэффициента непрозрачности, мы ограничимся записью основных приближенных соотношений.
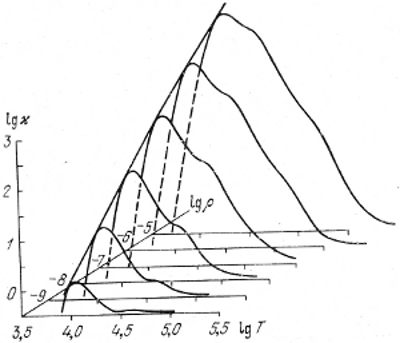
Рис. 1. График зависимости коэффициента непрозрачности от температуры и плотности газа.
Крутой склон слева - область неполной ионизации (формула (4.22)). Правая спадающая часть кривых - область формулы Крамерса, асимптоты - область томсоновского рассеяния (4.21).
Но прежде о характере этих соотношений. Вероятность термоядерных реакций определяется в первую очередь проникновением реагирующих ядер через потенциальный барьер. Соответствующий член в выражении для е имеет сложную экспоненциальную зависимость от температуры. Предэкспоненциальный множитель также зависит от температуры, кроме того, зависит от плотности, от наличия определенных и не всегда известных резонансов взаимодействия ядер и от химического состава. Эти зависимости не всегда удается представить в аналитическом виде. Усложняет задачу и необходимость учета некоторых поправок. Тем не менее и тут можно записать для величины е приближенные формулы в виде степенных зависимостей:
|
|
(4.24) |
Здесь ε0 зависит только от химического состава, m и n - некоторые числа, которые могут слабо изменяться с температурой. Зависимость ε0 от химического состава определяется не только полной концентрацией тяжелых элементов, но и относительным содержанием различных ядер, как, например, гелий-3, азот, углерод и т. п. Поэтому мы не будем выписывать явных зависимостей ε0 от химического состава. Более того, не будем приводить и численных значений ε0, отсылая читателя за подробностями к цитированным статьям Ривса. Заметим только, что в определении величины ε0 еще много неоднозначностей.
Параметр m определяется просто. Если основная реакция в цепи представляет собой столкновение двух ядер, то m = 1. В случае реакции, происходящей при одновременном столкновении трех ядер, m = 2. Параметр n определяется прохождением ядер через потенциальный барьер. Для реакции со столкновением двух ядер имеем для показателя n следующую зависимость:
|
|
(4.25) |
где Z1e и Z2e - заряды реагирующих ядер, m12 = m1m2/(m1+m2) - их приведенная масса. Видно, что показатель n зависит от температуры, но эта зависимость относительно слабая и в определенном интервале температур величину n можно считать постоянной.
При построении моделей на основе принципа подобия параметры ε0, m и n считаются постоянными по всей звезде. Хотя в действительности это и не так, но на самом деле возникающая здесь ошибка невелика, поскольку выделение энергии сосредоточено в очень малых областях, где изменения этих параметров совсем не существенны (см. ниже).
Известно несколько термоядерных реакций, имеющих существенное значение для энергетики звезд. Ниже мы их перечислим и приведем соответствующие значения параметров m и n.
1. Протон-протонный цикл. Из четырех протонов образуется ядро Не4. В промежуточных стадиях появляются ядра Н2, Не3, Li7, Be7 и Be8, а также В8. Реакция с бериллием и бором ответственна за излучение нейтрино Солнцем. Основная реакция цикла - образование дейтерия из двух протонов. Здесь m = 1 и
|
|
(4.26) |
Выражение T6 означает, что температура записана в миллионах градусов. Реакция протон-протонного цикла доминирует при относительно низких температурах (T6 ≈ 10-18). Здесь n ≈ 4.
2. Углеродно-азотно-кислородный цикл. Из четырех протонов также образуется ядро гелия, по теперь в промежуточных реакциях принимают участие ядра С12, С13, N13, N14, N15, О15, О16, О17, F17. Скорость выделения энергии лимитируется реакцией соединения азота N14 и протона. Здесь, по-прежнему, m = 1, а
|
|
(4.27) |
Этот цикл существен при более высоких температурах (T6 ≳ 18) и показатель n ≈ 16.
Этими двумя циклами исчерпывается превращение водорода в гелий. Затем, при более высоких температурах, начинается превращение гелия в более тяжелые элементы.
3. Если примесь тяжелых элементов к обогащенному гелием веществу мала, то происходит процесс соединения трех ядер гелия в одно ядро углерода С12 при тройном столкновении. Поэтому m = 2. Показатель п определяется проникновением через барьер сложной системы трех ядер. В результате получаем
|
|
(4.28) |
где T8 - температура, выраженная в сотнях миллионов градусов. Эта реакция, как и другие гелиевые реакции, протекают при температурах, больших 0,7 ⋅ 108 градусов.
4. Если велико содержание углерода, то возможно поглощение гелия его ядрами с образованием кислорода. Аналогично, ядра азота могут также поглощать ядра гелия с образованием фтора; ядра кислорода, поглощая ядра гелия, образуют ядра неона и т. д. Во всех подобных реакциях m = 1 и параметр n при T8 ∼ 0,3-2
|
|
(4.29) |
С ростом номера ядра растет и показатель n . Для очень больших температур T8 ≥ 5 - 20 большой вклад вносят высокие уровни возбуждения ядер и показатель п обратно пропорционален температуре, т. е. быстрее уменьшается с ее ростом.
5. Наконец, при очень высоких температурах вступают в реакцию между собой и более тяжелые элементы. Из двух ядер углерода образуется ядро магния, из двух ядер кислорода образуется ядро серы. Здесь, по-прежнему, m = 1, а показатель п очень велик. Весьма приблизительно
|
|
(4.30) |
Еще раз отметим, что в статьях Ривса (в сборниках [9, 10]) даны более точные значения этих параметров.
Сильная зависимость мощности термоядерных источников от температуры означает, что в реальных звездах выделение энергии происходит в относительно небольшом объеме в центре звезды, либо в тонком слое, если источники энергии в центре звезды уже выгорели. И в том и в другом случае в этих областях температура меняется незначительно и поэтому можно считать параметр n постоянным. Иными словами, рассчитывая структуру отдельной звезды, можно исходить из формулы (4.24) с постоянными значениями m иn, но, переходя от одной звезды к другой, можно менять значение показателя n в соответствии с характерной температурой той области, где происходит генерация энергии в этих звездах.
Именно поэтому мы привели здесь столь подробные данные о показателях n. Теперь у нас есть основные уравнения и их параметры, описывающие структуру звезды. Правда, эти уравнения надо еще написать в более удобном виде и сформулировать граничные условия. Это будет сделано в следующих параграфах при рассмотрении конкретных примеров.
<< § 3.5 Выражение массы и светимости звезд через мировые постоянные | Оглавление | § 4.2 Политропные и конвективные звезды >>